הבדלים בין גרסאות בדף "תרגול 10 תשעז"
(←יחסי שקילות) |
|||
| (14 גרסאות ביניים של 4 משתמשים אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
==יחסי שקילות== | ==יחסי שקילות== | ||
| − | הגדרה: תהא A קבוצה ו-R יחס עליה. R | + | הגדרה: תהא <math>A</math> קבוצה ו-<math>R</math> יחס עליה. <math>R</math> יקרא '''יחס שקילות''' (יח"ש) אם הוא |
#רפלקסיבי | #רפלקסיבי | ||
#סימטרי | #סימטרי | ||
| שורה 8: | שורה 8: | ||
'''סימון מקובל:''' | '''סימון מקובל:''' | ||
| + | אם <math>R</math> יחס שקילות מסמנים גם <math>x \sim y</math> עבור <math>(x,y)\in R</math>. | ||
| − | + | וכן נסמן <math>(A,\sim)</math> את הקבוצה עם יחס השקילות. | |
| − | + | ====תרגיל==== | |
| − | + | על <math>\mathbb{R}</math> נגדיר ארבעה יחסים <math>Q,R,S,T</math> באופן הבא: לכל <math>x,y\in \mathbb{R}</math>: | |
| − | + | <math>xQy\iff x-y=17</math> | |
| − | + | <math>xRy\iff x-y\in \mathbb{N}\cup \{0\}</math> | |
| − | + | <math>xSy\iff x-y\in 2\mathbb{Z}\cup 3\mathbb{Z}</math>. | |
| − | + | <math>xTy\iff x-y\in \mathbb{Z}</math>. | |
| − | + | בדקו עבור כל אחד מהם האם הוא יחס שקילות. | |
| − | + | =====פתרון===== | |
| − | + | ||
| − | + | <math>Q</math> לא כיון שלא רפלקסיבי, שהרי לכל <math>x\in \mathbb{R}</math> (ובפרט קיים לפחות אחד) <math>x-x=0\neq 17</math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <math>R</math> אמנם רפלקסיבי, אך לא סימטרי. | |
| − | + | <math>S</math> לא טרנזיטיבי: <math>2S6\land 6S3</math> אבל לא נכון ש-<math>2S3</math>. | |
| − | + | <math>T</math> כן יחס שקילות: | |
| − | + | ||
| + | רפלקסיביות: יהי <math>x\in \mathbb{R}</math>, אז <math>x-x=0\in \mathbb{Z}</math>. | ||
| − | + | סימטריות: <math>xTy\Rightarrow \exists a\in \mathbb{Z} :x-y=a \Rightarrow y-x=-a\in \mathbb{Z} \Rightarrow yTx</math>. | |
| − | + | טרנזיטיביות: <math>xTy\land yTz\Rightarrow \exists a\in \mathbb{Z}: x-y=a \land \exists b\in \mathbb{Z}: y-z=b\\ \Rightarrow x-z=x-y+y-z=a+b\in \mathbb{Z}</math>. | |
| − | + | ||
| + | ===מחלקות שקילות וחלוקה=== | ||
| − | משפט: יהא R יחס שקילות על A אזי | + | הגדרה: תהא <math>A</math> קבוצה. '''חלוקה''' של <math>A</math> היא אוסף של תת קבוצות זרות של <math>A</math> המכסות את <math>A</math>. באופן פורמלי קיימות תת קבוצות <math>\{A_i\}_{i\in I}</math> |
| − | # לכל <math>x,y\in A</math> מתקיים <math>[x]=[y]</math> או <math>[x]\cap [y] =\ | + | כך שמתקיים: |
| − | # <math>A=\bigcup_{[x]\in A/R}[x]</math> | + | * <math>\forall i\in I: A_i \neq \varnothing </math>. |
| − | הערה: זה בדיוק אומר שמיחס שקילות ניתן להגיע לחלוקה של A | + | * <math>\bigcup _{i\in I} A_i =A </math> כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה. |
| + | * הקבוצות <math>A_i</math> הן '''זרות בזוגות'''. כלומר החיתוך בין כל שתי תת קבוצות הוא ריק (<math>\forall i\ne j\in I : A_i\cap A_j = \varnothing</math>). | ||
| + | |||
| + | הגדרה: | ||
| + | |||
| + | יהא <math>R</math> יחס שקילות על <math>A</math> אזי | ||
| + | |||
| + | # לכל <math>x\in A</math> מוגדרת '''מחלקת השקילות של <math>x</math>''' להיות <math>\bar{x}=[x]_R:=\{y\in A | (x,y)\in R\}</math>. | ||
| + | # ''' קבוצת המנה ''' מוגדרת <math>A/R := \{ [x]_R | x\in A\} </math>. | ||
| + | |||
| + | |||
| + | '''משפט''': יהא <math>R</math> יחס שקילות על <math>A</math> אזי | ||
| + | # לכל <math>x,y\in A</math> מתקיים <math>[x]=[y]</math> או <math>[x]\cap [y] =\varnothing </math> (כלומר מחלקות השקילות זרות). | ||
| + | # <math>A=\bigcup_{[x]\in A/R}[x]</math> (כלומר איחוד מחלקות השקילות הוא כל <math>A</math>). | ||
| + | הערה: זה בדיוק אומר שמיחס שקילות ניתן להגיע לחלוקה של <math>A</math>. | ||
מסקנה: | מסקנה: | ||
| − | תהא A קבוצה אזי יש התאמה {<math>R</math> יחס שקילות על A } | + | תהא <math>A</math> קבוצה אזי יש התאמה {<math>R</math> יחס שקילות על <math>A</math>} |
| − | <math>\leftrightarrow</math> {חלוקות של A} | + | <math>\leftrightarrow</math> {חלוקות של <math>A</math>}. |
חידוד: מהותו העיקרית של יחס שקילויות הוא לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת. | חידוד: מהותו העיקרית של יחס שקילויות הוא לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת. | ||
| + | |||
| + | ====תרגיל==== | ||
| + | ראינו לעיל יחס <math>T\subseteq \mathbb{R}\times \mathbb{R}</math> והראינו שהוא יחס שקילות. הוכיחו: | ||
| + | |||
| + | א. <math>x\in \mathbb{R}\smallsetminus \mathbb{Q}\Rightarrow [x]_T\subseteq \mathbb{R}\smallsetminus \mathbb{Q}</math>. | ||
| + | |||
| + | ב. אם <math>x,y\in [0,1)</math> שונים אז <math>[x]_T\neq [y]_T</math>. | ||
| + | |||
| + | ג. <math>\forall x\in \mathbb{R} \exists y\in [0,1): [x]_T=[y]_T</math>. | ||
| + | |||
| + | =====פתרון===== | ||
| + | א.נוכיח בשלילה: יהי <math>x\in \mathbb{R}\smallsetminus \mathbb{Q}</math> ונניח בשלילה שקיים <math>q\in \mathbb{Q}\cap [x]_T</math>. נקבל שקיים <math>a\in \mathbb{Z}</math> כך ש <math>x-q=a</math> ולכן <math>x=a+q\in \mathbb{Q}</math> בסתירה (סגירות הרציונאליים). | ||
| + | |||
| + | ב. בהינתן כל <math>x>y</math> ולכן <math>x-y>0</math> ומאידך, כיון ששניהם בין 0 ל-1 נקבל <math>x-y<1</math>, ולכן ההפרש בהכרח לא שלם, ולכן הם לא שקולים. | ||
| + | |||
| + | ג. כל מספר כשמחסרים ממנו את הערך השלם התחתון שלו מקבלים משהו בין 0 ל-1, והם שקולים כי ההפרש הוא הערך השלם התחתון, שהוא, מהגדרתו, מספר שלם. | ||
| + | |||
| + | ====תרגיל==== | ||
| + | |||
| + | על <math>\mathbb{R}\times \mathbb{R}</math> נגדיר יחס <math>\sim</math> לפי זה שלכל <math>(x_1,y_1),(x_2,y_2)</math>: | ||
| + | |||
| + | <math>(x_1,y_1)\sim (x_2,y_2)\iff x_1^2+y_1^2=x_2^2+y_2^2</math>. | ||
| + | |||
| + | קל לראות שזהו יחס שקילות. מהי, מבחינה גיאומטרית מחלקת השקילות של <math>(0,1)</math>? ומהי, מבחינה גיאומטרית, קבוצת המנה? | ||
| + | |||
| + | =====פתרון===== | ||
| + | |||
| + | מעגל עם רדיוס 1 מסביב לראשית. קבוצת המנה - אוסף המעגלים מסביב לראשית. | ||
גרסה אחרונה מ־14:35, 16 ביולי 2019
חזרה לדף מערכי התרגול.
תוכן עניינים
יחסי שקילות
הגדרה: תהא  קבוצה ו-
קבוצה ו- יחס עליה.
יחס עליה.  יקרא יחס שקילות (יח"ש) אם הוא
יקרא יחס שקילות (יח"ש) אם הוא
- רפלקסיבי
- סימטרי
- טרנזיטיבי
סימון מקובל:
אם  יחס שקילות מסמנים גם
יחס שקילות מסמנים גם 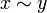 עבור
עבור 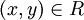 .
.
וכן נסמן 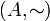 את הקבוצה עם יחס השקילות.
את הקבוצה עם יחס השקילות.
תרגיל
על 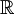 נגדיר ארבעה יחסים
נגדיר ארבעה יחסים 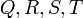 באופן הבא: לכל
באופן הבא: לכל 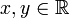 :
:
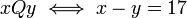
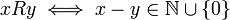
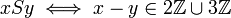 .
.
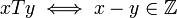 .
.
בדקו עבור כל אחד מהם האם הוא יחס שקילות.
פתרון
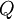 לא כיון שלא רפלקסיבי, שהרי לכל
לא כיון שלא רפלקסיבי, שהרי לכל 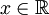 (ובפרט קיים לפחות אחד)
(ובפרט קיים לפחות אחד) 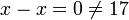 .
.
 אמנם רפלקסיבי, אך לא סימטרי.
אמנם רפלקסיבי, אך לא סימטרי.
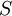 לא טרנזיטיבי:
לא טרנזיטיבי: 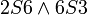 אבל לא נכון ש-
אבל לא נכון ש-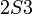 .
.
 כן יחס שקילות:
כן יחס שקילות:
רפלקסיביות: יהי 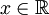 , אז
, אז 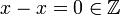 .
.
סימטריות: 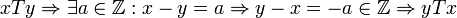 .
.
טרנזיטיביות: עיבוד הנוסחה נכשל (שגיאת תחביר): xTy\land yTz\Rightarrow \exists a\in \mathbb{Z}: x-y=a \land \exists b\in \mathbb{Z}: y-z=b\\ \Rightarrow x-z=x-y+y-z=a+b\in \mathbb{Z} .
מחלקות שקילות וחלוקה
הגדרה: תהא  קבוצה. חלוקה של
קבוצה. חלוקה של  היא אוסף של תת קבוצות זרות של
היא אוסף של תת קבוצות זרות של  המכסות את
המכסות את  . באופן פורמלי קיימות תת קבוצות
. באופן פורמלי קיימות תת קבוצות 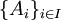 כך שמתקיים:
כך שמתקיים:
-
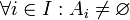 .
. -
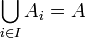 כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה.
כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה. - הקבוצות
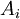 הן זרות בזוגות. כלומר החיתוך בין כל שתי תת קבוצות הוא ריק (
הן זרות בזוגות. כלומר החיתוך בין כל שתי תת קבוצות הוא ריק (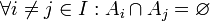 ).
).
הגדרה:
יהא  יחס שקילות על
יחס שקילות על  אזי
אזי
- לכל
 מוגדרת מחלקת השקילות של
מוגדרת מחלקת השקילות של  להיות
להיות ![\bar{x}=[x]_R:=\{y\in A | (x,y)\in R\}](/images/math/3/e/c/3ec2682e1e1f10cf21a983d1a44b2f96.png) .
. - קבוצת המנה מוגדרת
![A/R := \{ [x]_R | x\in A\}](/images/math/4/c/5/4c58650f9531733c432c54f74881db01.png) .
.
משפט: יהא  יחס שקילות על
יחס שקילות על  אזי
אזי
- לכל
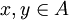 מתקיים
מתקיים ![[x]=[y]](/images/math/6/3/b/63be84aae0ca1995af2d779096090fdc.png) או
או ![[x]\cap [y] =\varnothing](/images/math/4/9/8/4982f0ad0ef04caa177a3b518832906a.png) (כלומר מחלקות השקילות זרות).
(כלומר מחלקות השקילות זרות). -
![A=\bigcup_{[x]\in A/R}[x]](/images/math/3/3/2/3323ab7c4ddf604cede7985587f3c401.png) (כלומר איחוד מחלקות השקילות הוא כל
(כלומר איחוד מחלקות השקילות הוא כל  ).
).
הערה: זה בדיוק אומר שמיחס שקילות ניתן להגיע לחלוקה של  .
.
מסקנה:
תהא  קבוצה אזי יש התאמה {
קבוצה אזי יש התאמה { יחס שקילות על
יחס שקילות על  }
}
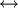 {חלוקות של
{חלוקות של  }.
}.
חידוד: מהותו העיקרית של יחס שקילויות הוא לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת.
תרגיל
ראינו לעיל יחס 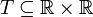 והראינו שהוא יחס שקילות. הוכיחו:
והראינו שהוא יחס שקילות. הוכיחו:
א. ![x\in \mathbb{R}\smallsetminus \mathbb{Q}\Rightarrow [x]_T\subseteq \mathbb{R}\smallsetminus \mathbb{Q}](/images/math/3/a/8/3a8605964b3dd79c68f563f509827a9e.png) .
.
ב. אם 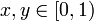 שונים אז
שונים אז ![[x]_T\neq [y]_T](/images/math/5/0/b/50b8153d3afe89b50d627584bc7058bf.png) .
.
ג. ![\forall x\in \mathbb{R} \exists y\in [0,1): [x]_T=[y]_T](/images/math/9/1/a/91a334058395d7f5ceca72b0d5aed47c.png) .
.
פתרון
א.נוכיח בשלילה: יהי 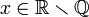 ונניח בשלילה שקיים
ונניח בשלילה שקיים ![q\in \mathbb{Q}\cap [x]_T](/images/math/6/b/8/6b8e0ff0c2c53dc1e0715f49c82173f2.png) . נקבל שקיים
. נקבל שקיים 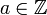 כך ש
כך ש 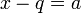 ולכן
ולכן 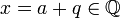 בסתירה (סגירות הרציונאליים).
בסתירה (סגירות הרציונאליים).
ב. בהינתן כל 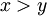 ולכן
ולכן 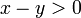 ומאידך, כיון ששניהם בין 0 ל-1 נקבל
ומאידך, כיון ששניהם בין 0 ל-1 נקבל 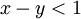 , ולכן ההפרש בהכרח לא שלם, ולכן הם לא שקולים.
, ולכן ההפרש בהכרח לא שלם, ולכן הם לא שקולים.
ג. כל מספר כשמחסרים ממנו את הערך השלם התחתון שלו מקבלים משהו בין 0 ל-1, והם שקולים כי ההפרש הוא הערך השלם התחתון, שהוא, מהגדרתו, מספר שלם.
תרגיל
על 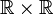 נגדיר יחס
נגדיר יחס 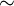 לפי זה שלכל
לפי זה שלכל 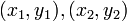 :
:
 .
.
קל לראות שזהו יחס שקילות. מהי, מבחינה גיאומטרית מחלקת השקילות של 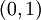 ? ומהי, מבחינה גיאומטרית, קבוצת המנה?
? ומהי, מבחינה גיאומטרית, קבוצת המנה?
פתרון
מעגל עם רדיוס 1 מסביב לראשית. קבוצת המנה - אוסף המעגלים מסביב לראשית.