הבדלים בין גרסאות בדף "תרגול 10 תשעז"
(יצירת דף עם התוכן "'''הגדרות.''' יהיו A קבוצה, B קבוצה המוכלת בה וR יחס סדר חלקי: *חסם מלעיל של B הוא איבר <math>x\in A</mat...") |
|||
| שורה 28: | שורה 28: | ||
'''הגדרה.''' יהי R יחס סדר חלקי על A. אם לכל שני איברים a,b בA מתקיים <math>[(a,b)\in R]\or[(b,a)\in R]</math> אזי R נקרא '''יחס סדר מלא'''. | '''הגדרה.''' יהי R יחס סדר חלקי על A. אם לכל שני איברים a,b בA מתקיים <math>[(a,b)\in R]\or[(b,a)\in R]</math> אזי R נקרא '''יחס סדר מלא'''. | ||
| − | + | למשל: היחס 'קטן שווה' על השלמים/הממשיים הוא יחס סדר מלא. | |
| − | + | שימו לב כי זו דוגמא ליחס סדר בלי איברים מינימליים או מקסימליים. | |
| − | + | ||
| − | + | ===יחסי שקילות=== | |
| + | הגדרה: תהא A קבוצה ו-R יחס עליה. R יקרה יחס שקילות אם הוא | ||
| + | #רפלקסיבי | ||
| + | #סימטרי | ||
| + | #טרנזיטיבי | ||
| − | + | דוגמא: תהא <math>A=\{1,2,3,4,5,6\}</math>. נגדיר תת הקבוצות <math>A_1=\{1,3\},A_2=\{2,4,5\},A_3=\{6\}</math> | |
| − | + | נגדיר יחס R על A כך <math>\exist 1\leq i \leq 3 : x,y\in A_i \Leftrightarrow xRy</math> | |
| − | + | טענה R יחס שקילות | |
| − | + | הוכחה: | |
| − | + | ||
| − | + | ||
| − | <math> | + | 1. רפלקסיביות - נניח <math>x\in A</math> לכן x שייך ל <math>A_i</math> עבור i מסוים (שכן האיחוד שלהן שווה לA) ולכן <math>(x,x)\in R</math>. |
| − | + | 2. סימטריות - נניח <math>(x,y)\in R</math> אזי <math>x,y\in A_i</math> עבור i מסוים, מכיוון שאין משמעות לסדר שייכות לקבוצה, נובע שגם <math>(y,x)\in R</math>. | |
| − | + | 3. טרנזיטיביות - נניח <math>[(x,y)\in R] \and [(y,z)\in R]</math> אזי קיימים i,j כך ש <math>x,y\in Aֹ_i</math> וגם <math>y,z\in A_j</math>. לכן <math>y\in A_i\cap A_j</math>. מכיוון שהחיתוך בין תתי הקבוצות הוא ריק מוכרח להיות ש<math>A_i=A_j</math> ולכן <math>x,y,z\in A_i</math> ולכן <math>(x,z)\in R</math> כפי שרצינו. | |
| − | |||
| − | + | הגדרה: תהא A קבוצה. '''חלוקה''' של A היא חלוקה של A לקבוצות זרות. באופן פורמלי קיימות תת קבוצות <math>\{A_i\}_{i\in I}</math> | |
| + | כך ש: | ||
| + | * <math>\forall i\in I: A_i \neq \emptyset </math> | ||
| + | * <math>\cup _{i\in I} A_i =A </math> כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה | ||
| + | * הקבוצות <math>A_i</math> הן '''זרות''' זו לו = החיתוך בין כל שתי תתי קבוצות הוא ריק (<math>\forall i\not= j\in I : A_i\cap A_j = \phi </math>) | ||
| − | + | כפי שראינו בדוגמה הקודמת חלוקה של A מגדירה יחס שקילות (אמנם זה "רק" דוגמא אבל ניתן להוכיח את המקרה הכללי באותו אופן). | |
| − | <math> | + | |
| + | דוגמא נוספת: | ||
| + | |||
| + | נגדיר יחס שקילות R על <math>\mathbb{Z}</math> ע"י <math>3|(x-y) \Leftrightarrow xRy</math> | ||
| + | |||
| + | טענה: R אכן יחס שקילות | ||
| + | |||
| + | הוכחה: | ||
| + | |||
| + | 1. רפלקסיביות - נניח <math>\forall x\in \mathbb{Z}:3|0=x-x</math> לכן <math>xRx</math> | ||
| + | |||
| + | 2. סימטריות - נניח <math>(x,y)\in R</math> אזי <math>3|(x-y)</math> ולכן גם <math>3|(y-x)=-(x-y)</math> | ||
| + | |||
| + | 3. טרנזיטיביות - נניח <math>[(x,y)\in R] \and [(y,z)\in R]</math> אזי <math>3|(x-y)\and 3|(y-z) </math> | ||
| + | ולכן גם <math>3|(z-x)=(z-y)+(y-x)</math> | ||
| + | |||
| + | |||
| + | הגדרה: | ||
| + | |||
| + | יהא R יחס שקילות על A אזי | ||
| + | |||
| + | # לכל <math>x\in A</math> מוגדרת '''מחלקת השקילות של x ''' להיות <math>\bar{x}=[x]_R:=\{y\in A | (x,y)\in R\} </math> | ||
| + | # ''' קבוצת המנה ''' מוגדרת <math>A/R := \{ [x]_R | x\in A\} </math> | ||
| + | |||
| + | |||
| + | למשל, בדוגמא הראשונה <math>A_1,A_2,A_3</math> הן מחלקות השקילות. קבוצת המנה היא <math>A/R=\{A_1,A_2,A_3\}</math> | ||
| + | |||
| + | בדוגמא השניה מחלקת השקילות של 0 היא <math>[0]_R=\{ 0 \pm 3 \pm 6 \dots \}</math> וקבוצת המנה היא | ||
| + | <math>\mathbb{Z}/R= \{[0]_R,[1]_R,[2]_R\}</math> (כלומר כל השאריות האפשריות בחלוקה ב-3). | ||
| + | |||
| + | |||
| + | משפט: יהא R יחס שקילות על A אזי | ||
| + | # לכל <math>x,y\in A</math> מתקיים <math>[x]=[y]</math> או <math>[x]\cap [y] =\phi </math> (כלומר מחלקות השקילות זרות) | ||
| + | # <math>A=\bigcup_{[x]\in A/R}[x]</math> כלומר (איחוד מחלקות השקילות תתן את כל A) | ||
| + | הערה: זה בדיוק אומר שמיחס שקילות ניתן להגיע לחלוקה של A | ||
| + | |||
| + | |||
| + | מסקנה: | ||
| + | תהא A קבוצה אזי יש התאמה {<math>R</math> יחס שקילות על A } | ||
| + | <math>\leftrightarrow</math> {חלוקות של A} | ||
| + | |||
| + | חידוד: מהותו העיקרית של יחס שקילויות הוא לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת. | ||
גרסה מ־10:20, 17 בינואר 2017
הגדרות. יהיו A קבוצה, B קבוצה המוכלת בה וR יחס סדר חלקי:
- חסם מלעיל של B הוא איבר
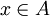 כך שמתקיים
כך שמתקיים 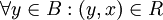
- חסם מלרע של B הוא איבר
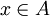 כך שמתקיים
כך שמתקיים 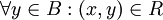
- החסם העליון (סופרמום) של B הינו המינימום של קבוצת חסמי המלעיל (אם קיים). מסומן
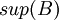
- החסם התחתון (אינפימום) של B הינו המקסימום של קבוצת חסמי המלרע (אם קיים). מסומן
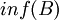
דוגמאות
דוגמא. נביט בקבוצת הטבעיים, ובתת קבוצה סופית שלה B. נביט ביחס "מחלק את". הסופרמום של B הוא המכפלה המשותפת המינימלית (lcm), והאינפימום הוא המחלק המשותף המקסימלי(gcd).
למשל 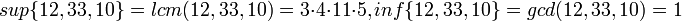
דוגמא
עבור 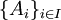 אוסף קבוצות. החסם העליון שלה הוא (ביחס להכלה) הוא
אוסף קבוצות. החסם העליון שלה הוא (ביחס להכלה) הוא
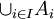
דוגמא.
נביט בקבוצה 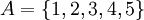 ונגדיר עליה יחס סדר חלקי:
ונגדיר עליה יחס סדר חלקי:
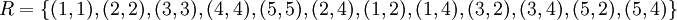
(הזוגיים 'גדולים' מכל אי הזוגיים ומהזוגיים הקטנים מהם)
נביט בתת הקבוצה המכילה את המספרים האי זוגיים בלבד 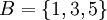 . קבוצת חסמי המלעיל של B הינה
. קבוצת חסמי המלעיל של B הינה 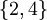 . המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.
. המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.
הגדרה. יהי R יחס סדר חלקי על A. אם לכל שני איברים a,b בA מתקיים ![[(a,b)\in R]\or[(b,a)\in R]](/images/math/1/d/4/1d4d3394750a0b97771353ed8775b927.png) אזי R נקרא יחס סדר מלא.
אזי R נקרא יחס סדר מלא.
למשל: היחס 'קטן שווה' על השלמים/הממשיים הוא יחס סדר מלא. שימו לב כי זו דוגמא ליחס סדר בלי איברים מינימליים או מקסימליים.
יחסי שקילות
הגדרה: תהא A קבוצה ו-R יחס עליה. R יקרה יחס שקילות אם הוא
- רפלקסיבי
- סימטרי
- טרנזיטיבי
דוגמא: תהא 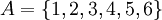 . נגדיר תת הקבוצות
. נגדיר תת הקבוצות 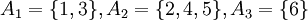
נגדיר יחס R על A כך 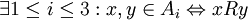
טענה R יחס שקילות
הוכחה:
1. רפלקסיביות - נניח 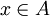 לכן x שייך ל
לכן x שייך ל 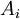 עבור i מסוים (שכן האיחוד שלהן שווה לA) ולכן
עבור i מסוים (שכן האיחוד שלהן שווה לA) ולכן 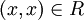 .
.
2. סימטריות - נניח 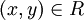 אזי
אזי 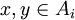 עבור i מסוים, מכיוון שאין משמעות לסדר שייכות לקבוצה, נובע שגם
עבור i מסוים, מכיוון שאין משמעות לסדר שייכות לקבוצה, נובע שגם 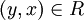 .
.
3. טרנזיטיביות - נניח ![[(x,y)\in R] \and [(y,z)\in R]](/images/math/0/b/e/0be7ba4e28716aaf8c19a241b4c93189.png) אזי קיימים i,j כך ש
אזי קיימים i,j כך ש 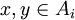 וגם
וגם 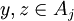 . לכן
. לכן 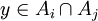 . מכיוון שהחיתוך בין תתי הקבוצות הוא ריק מוכרח להיות ש
. מכיוון שהחיתוך בין תתי הקבוצות הוא ריק מוכרח להיות ש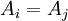 ולכן
ולכן 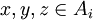 ולכן
ולכן 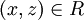 כפי שרצינו.
כפי שרצינו.
הגדרה: תהא A קבוצה. חלוקה של A היא חלוקה של A לקבוצות זרות. באופן פורמלי קיימות תת קבוצות 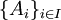 כך ש:
כך ש:
-
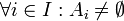
-
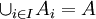 כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה
כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה - הקבוצות
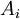 הן זרות זו לו = החיתוך בין כל שתי תתי קבוצות הוא ריק (
הן זרות זו לו = החיתוך בין כל שתי תתי קבוצות הוא ריק (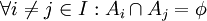 )
)
כפי שראינו בדוגמה הקודמת חלוקה של A מגדירה יחס שקילות (אמנם זה "רק" דוגמא אבל ניתן להוכיח את המקרה הכללי באותו אופן).
דוגמא נוספת:
נגדיר יחס שקילות R על 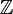 ע"י
ע"י 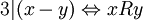
טענה: R אכן יחס שקילות
הוכחה:
1. רפלקסיביות - נניח 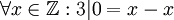 לכן
לכן 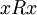
2. סימטריות - נניח 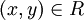 אזי
אזי 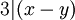 ולכן גם
ולכן גם 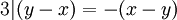
3. טרנזיטיביות - נניח ![[(x,y)\in R] \and [(y,z)\in R]](/images/math/0/b/e/0be7ba4e28716aaf8c19a241b4c93189.png) אזי
אזי 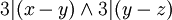 ולכן גם
ולכן גם 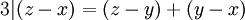
הגדרה:
יהא R יחס שקילות על A אזי
- לכל
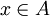 מוגדרת מחלקת השקילות של x להיות
מוגדרת מחלקת השקילות של x להיות ![\bar{x}=[x]_R:=\{y\in A | (x,y)\in R\}](/images/math/3/e/c/3ec2682e1e1f10cf21a983d1a44b2f96.png)
- קבוצת המנה מוגדרת
![A/R := \{ [x]_R | x\in A\}](/images/math/4/c/5/4c58650f9531733c432c54f74881db01.png)
למשל, בדוגמא הראשונה 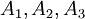 הן מחלקות השקילות. קבוצת המנה היא
הן מחלקות השקילות. קבוצת המנה היא 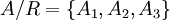
בדוגמא השניה מחלקת השקילות של 0 היא ![[0]_R=\{ 0 \pm 3 \pm 6 \dots \}](/images/math/2/5/9/2598a70b2805b479700f0e7e2dceff56.png) וקבוצת המנה היא
וקבוצת המנה היא
![\mathbb{Z}/R= \{[0]_R,[1]_R,[2]_R\}](/images/math/b/0/6/b06f29fa198c69e36280452ef86cb9e9.png) (כלומר כל השאריות האפשריות בחלוקה ב-3).
(כלומר כל השאריות האפשריות בחלוקה ב-3).
משפט: יהא R יחס שקילות על A אזי
- לכל
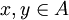 מתקיים
מתקיים ![[x]=[y]](/images/math/6/3/b/63be84aae0ca1995af2d779096090fdc.png) או
או ![[x]\cap [y] =\phi](/images/math/2/8/5/285cdd0729559197bf11c30df83a2f8f.png) (כלומר מחלקות השקילות זרות)
(כלומר מחלקות השקילות זרות) -
![A=\bigcup_{[x]\in A/R}[x]](/images/math/3/3/2/3323ab7c4ddf604cede7985587f3c401.png) כלומר (איחוד מחלקות השקילות תתן את כל A)
כלומר (איחוד מחלקות השקילות תתן את כל A)
הערה: זה בדיוק אומר שמיחס שקילות ניתן להגיע לחלוקה של A
מסקנה:
תהא A קבוצה אזי יש התאמה {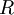 יחס שקילות על A }
יחס שקילות על A }
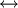 {חלוקות של A}
{חלוקות של A}
חידוד: מהותו העיקרית של יחס שקילויות הוא לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת.