תרגול 10 תשעז
הגדרות. יהיו A קבוצה, B קבוצה המוכלת בה וR יחס סדר חלקי:
- חסם מלעיל של B הוא איבר
 כך שמתקיים
כך שמתקיים 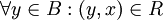
- חסם מלרע של B הוא איבר
 כך שמתקיים
כך שמתקיים 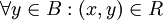
- החסם העליון (סופרמום) של B הינו המינימום של קבוצת חסמי המלעיל (אם קיים). מסומן
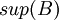
- החסם התחתון (אינפימום) של B הינו המקסימום של קבוצת חסמי המלרע (אם קיים). מסומן
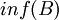
דוגמאות
דוגמא. נביט בקבוצת הטבעיים, ובתת קבוצה סופית שלה B. נביט ביחס "מחלק את". הסופרמום של B הוא המכפלה המשותפת המינימלית (lcm), והאינפימום הוא המחלק המשותף המקסימלי(gcd).
למשל 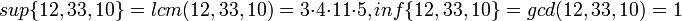
דוגמא
עבור 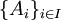 אוסף קבוצות. החסם העליון שלה הוא (ביחס להכלה) הוא
אוסף קבוצות. החסם העליון שלה הוא (ביחס להכלה) הוא
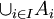
דוגמא.
נביט בקבוצה 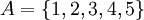 ונגדיר עליה יחס סדר חלקי:
ונגדיר עליה יחס סדר חלקי:
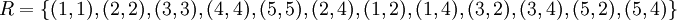
(הזוגיים 'גדולים' מכל אי הזוגיים ומהזוגיים הקטנים מהם)
נביט בתת הקבוצה המכילה את המספרים האי זוגיים בלבד 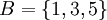 . קבוצת חסמי המלעיל של B הינה
. קבוצת חסמי המלעיל של B הינה 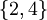 . המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.
. המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.
הגדרה. יהי R יחס סדר חלקי על A. אם לכל שני איברים a,b בA מתקיים ![[(a,b)\in R]\or[(b,a)\in R]](/images/math/1/d/4/1d4d3394750a0b97771353ed8775b927.png) אזי R נקרא יחס סדר מלא.
אזי R נקרא יחס סדר מלא.
תרגיל (ממבחן קיץ תשעה מועד ב)
תהא 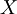 קבוצת כל הסדרות הבינאריות (סדרה בינארית היא
קבוצת כל הסדרות הבינאריות (סדרה בינארית היא 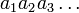 כאשר
כאשר 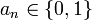 ). נגדיר יחס
). נגדיר יחס  על
על 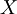 כך:
עבור
כך:
עבור 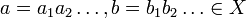
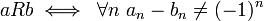
א. הוכיחו ש  יחס סדר על
יחס סדר על 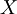
ב. קבעו האם  יחס סדר מלא על
יחס סדר מלא על 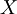
ג. מצאו (אם קיימים) איבר קטן וגדול ביותר ב 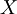 (ביחס ל
(ביחס ל  )
)
פתרון
דרך שקולה לתאר את היחס שמפשטת את השאלה היא כך
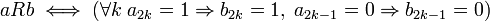
כלומר במיקומים הזוגיים, אם a שווה 1 אז זה גורר ש b שווה 1
ובמיקומים האי זוגיים, אם a שווה 0 אז זה גורר ש b שווה 0
א. תרגיל לבד!
ב. לא סדר מלא, למשל 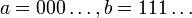 לא מתייחסים זה לזה.
לא מתייחסים זה לזה.
ג. קימיים, 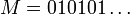 הינו איבר הגדול ביותר כי לכל
הינו איבר הגדול ביותר כי לכל  מתקים
מתקים 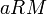
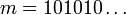 הינו איבר קטן ביותר כי לכל
הינו איבר קטן ביותר כי לכל  מתקים
מתקים