תרגול 11 תשעז
חזרה לדף מערכי התרגול.
יחסי שקילות - תרגילים נוספים
תרגיל
תהא 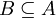 קבוצה ותת קבוצה. נגדיר יחס
קבוצה ותת קבוצה. נגדיר יחס 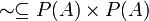 ע"י
ע"י 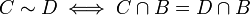 . הוכיחו:
. הוכיחו:
א. זהו יחס שקילות.
ב. לכל 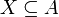 קיימת
קיימת 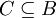 כך ש
כך ש ![[X]_R=[C]_R](/images/math/f/9/f/f9f186863380c9741a8790cd51795a35.png) .
.
ג. אם 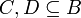 שונות, אז
שונות, אז ![[C]\neq [D]](/images/math/d/9/4/d94bc9f892b98c2e5bd2839944c4bc4a.png) .
.
פיתרון
א. רפלקסיביות: כמובן ש- 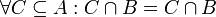 , ולכן
, ולכן 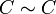 .
.
סימטריות: נניח 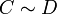 אזי
אזי 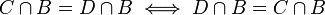 , ולכן
, ולכן 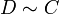 .
.
טרנזיטיביות: נניח 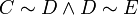 אזי
אזי 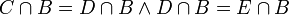 ומטרנזיטיביות יחס השיוויון נקבל הדרוש.
ומטרנזיטיביות יחס השיוויון נקבל הדרוש.
ב. יהי 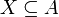 נשים לב שמתקיים
נשים לב שמתקיים 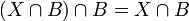 ולכן
ולכן ![[X]_R=[X\cap B]_R](/images/math/f/e/f/fef9dfa29fd8f0d841d8751bd8398521.png) , ובנוסף מתקיים
, ובנוסף מתקיים 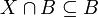 ולכן נוכל לבחור
ולכן נוכל לבחור 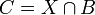 .
.
ג. תהיינה 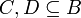 שונות. לכן קיים (בה"כ)
שונות. לכן קיים (בה"כ) 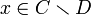 וכמובן
וכמובן 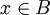 , ולכן נקבל
, ולכן נקבל 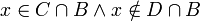 כלומר
כלומר 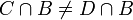 ולכן
ולכן ![[C]\neq [D]](/images/math/d/9/4/d94bc9f892b98c2e5bd2839944c4bc4a.png) .
.
שאלה ממבחן
א. תהי  קבוצה לא ריקה ותהי
קבוצה לא ריקה ותהי 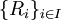 משפחה של יחסי שקילות על
משפחה של יחסי שקילות על  . הוכיחו כי החיתוך הכללי
. הוכיחו כי החיתוך הכללי 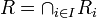 הינו יחס שקילויות על
הינו יחס שקילויות על  .
.
ב. נסמן 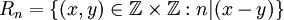 . מהם
. מהם 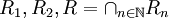 ? מהן קבוצות המנה
? מהן קבוצות המנה 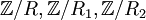 ?
?
פתרון
א. רפלקסיביות: מאחר ו-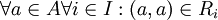 נובע ש-
נובע ש-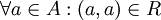 .
.
סימטריות: נניח 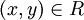 לכן
לכן 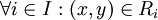 ולכן נובע מסמטריות היחסים ש
ולכן נובע מסמטריות היחסים ש 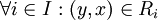 ולכן
ולכן 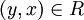 .
.
טרנזיטיביות: נניח 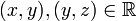 אזי
אזי 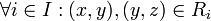 , וכיון שהוא יחס שקילות אז נובע
, וכיון שהוא יחס שקילות אז נובע 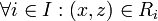 , ולפי הגדרת החיתוך הכללי נקבל
, ולפי הגדרת החיתוך הכללי נקבל 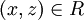
ב. 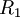 הינו אוסף כל הזוגות הסדורים מעל השלמים, שכן אחד מחלק כל מספר ולכן כל הפרש.
הינו אוסף כל הזוגות הסדורים מעל השלמים, שכן אחד מחלק כל מספר ולכן כל הפרש.
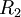 הינו אוסף כל הזוגות בהם שני הצדדים זוגיים או שני הצדדים אי זוגיים, שכן ההפרש בינהם חייב להיות זוגי.
הינו אוסף כל הזוגות בהם שני הצדדים זוגיים או שני הצדדים אי זוגיים, שכן ההפרש בינהם חייב להיות זוגי.
 הינו אוסף הזוגות שההפרש בינהם מתחלק בכל המספרים הטבעיים. רק הפרש אפס יכול להתחלק בכל מספר, ולכן
הינו אוסף הזוגות שההפרש בינהם מתחלק בכל המספרים הטבעיים. רק הפרש אפס יכול להתחלק בכל מספר, ולכן  הינו אוסף הזוגות מהצורה
הינו אוסף הזוגות מהצורה 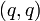 עבור
עבור 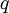 מספר שלם. (יחס השיוויון).
מספר שלם. (יחס השיוויון).
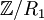 הינו אוסף מחלקות השקילות של היחס המכיל את כל הזוגות. יש בו רק מחלקת שקילות אחת המכילה את כל המספרים השלמים.
הינו אוסף מחלקות השקילות של היחס המכיל את כל הזוגות. יש בו רק מחלקת שקילות אחת המכילה את כל המספרים השלמים.
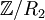 מכיל שתי קבוצות, קבוצת הזוגיים וקבוצת האי זוגיים שכן בין כל הזוגיים יש את היחס, ובין כל האי זוגיים ולא בין לבין כמובן (הרי זה יחס שקילויות כפי שקל להוכיח).
מכיל שתי קבוצות, קבוצת הזוגיים וקבוצת האי זוגיים שכן בין כל הזוגיים יש את היחס, ובין כל האי זוגיים ולא בין לבין כמובן (הרי זה יחס שקילויות כפי שקל להוכיח).
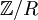 הינו אוסף כל הקבוצות המכילות איבר שלם בודד.
הינו אוסף כל הקבוצות המכילות איבר שלם בודד.