הבדלים בין גרסאות בדף "תרגול 11 תשעז"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏פתרון)
(←‏שאלה ממבחן)
שורה 32: שורה 32:
  
 
===שאלה ממבחן===
 
===שאלה ממבחן===
−
א. תהי A קבוצה לא ריקה ותהי <math>\{R_i\}_{i\in I}</math> משפחה של יחסי שקילות על A. הוכיחו כי החיתוך הכללי  <math>R=\cap_{i\in I}R_i</math> הינו יחס שקילויות על A.
+
תהי A קבוצה לא ריקה ותהי <math>\{R_i\}_{i\in I}</math> משפחה של יחסי שקילות על A. הוכיחו כי החיתוך הכללי  <math>R=\cap_{i\in I}R_i</math> הינו יחס שקילויות על A.
−
 
+
−
ב. נסמן <math>R_n=\{(x,y)\in\mathbb{Z}\times\mathbb{Z}:n|(x-y)\}</math>. מהם <math>R_1,R_2,R=\cap_{n\in\mathbb{N}}R_n</math>? מהן קבוצות המנה <math>\mathbb{Z}/R,\mathbb{Z}/R_1,\mathbb{Z}/R_2</math>?
+
  
 
====פתרון====
 
====פתרון====
−
א. רפלקסיביות: מאחר ו <math>\forall a\in A\forall i\in I : (a,a)\in R_i</math> נובע ש <math>\forall a\in A: (a,a)\in R</math>.
+
רפלקסיביות: מאחר ו <math>\forall a\in A\forall i\in I : (a,a)\in R_i</math> נובע ש <math>\forall a\in A: (a,a)\in R</math>.
−
 
+
  
 
סימטריות: נניח <math>(x,y)\in R</math> לכן <math>\forall i\in I:(x,y)\in R_i</math> ולכן נובע מסמטריות היחסים ש <math>\forall i\in I:(y,x)\in R_i</math> ולכן <math>(y,x)\in R</math>.
 
סימטריות: נניח <math>(x,y)\in R</math> לכן <math>\forall i\in I:(x,y)\in R_i</math> ולכן נובע מסמטריות היחסים ש <math>\forall i\in I:(y,x)\in R_i</math> ולכן <math>(y,x)\in R</math>.
  
 +
טרנזיטיביות: נניח <math>(x,y),(y,z)\in \mathbb R</math> אזי <math>\forall i\in I:(x,y),(y,z)\in R_i</math>, וכיון שהוא יחס שקילות אז נובע <math>\forall i\in I:(x,z)\in R_i</math>, ולפי הגדרת החיתוך הכללי נקבל <math>(x,z)\in R</math>
  
−
טרנזיטיביות: ממש אותו דבר...
+
===תרגיל===
−
 
+
תהא <math>B\subseteq A</math> קבוצה ותת קבוצה. נגדיר יחס <math>~subseteq P(A)\times P(A)</math> ע"י <math>C~D\iff C\cup B=D\cup B</math>. הוכח שזהו יחס שקילות.
−
 
+
−
ב. <math>R_1</math> הינו אוסף כל הזוגות הסדורים מעל השלמים, שכן אחד מחלק כל מספר ולכן כל הפרש.
+
−
 
+
−
<math>R_2</math> הינו אוסף כל הזוגות בהם שני הצדדים זוגיים או שני הצדדים אי זוגיים, שכן ההפרש בינהם חייב להיות זוגי.
+
−
 
+
−
R הינו אוסף הזוגות שההפרש בינהם מתחלק בכל המספרים הטבעיים. רק הפרש אפס יכול להתחלק בכל מספר, ולכן R הינו אוסף הזוגות מהצורה (q,q) עבור q מספר שלם. (יחס השיוויון.)
+
−
 
+
−
 
+
−
<math>\mathbb{Z}/R_1</math> הינו אוסף מחלקות השקילות של היחס המכיל את כל הזוגות. יש בו רק מחלקת שקילות אחת המכילה את כל המספרים השלמים.
+
−
 
+
−
<math>\mathbb{Z}/R_2</math> מכיל שתי קבוצות, קבוצת הזוגיים וקבוצת האי זוגיים שכן בין כל הזוגיים יש את היחס, ובין כל האי זוגיים ולא בין לבין כמובן (הרי זה יחס שקילויות כפי שקל להוכיח).
+
  
−
<math>\mathbb{Z}/R</math> הינו אוסף כל הקבוצות המכילות איבר שלם בודד.
+
====פיתרון====
 +
רפלקסיביות: כמובן ש- <math></math>

גרסה מ־09:59, 22 בינואר 2017

המשך יחסי שקילות

הגדרה: תהא A קבוצה. חלוקה של A היא חלוקה של A לקבוצות זרות. באופן פורמלי קיימות תת קבוצות 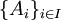\{A_i\}_{i\in I} כך ש:

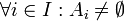
  • \forall i\in I: A_i \neq \emptyset
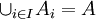  • \cup _{i\in I} A_i =A כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה
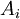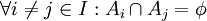  • הקבוצות A_i הן זרות זו לו = החיתוך בין כל שתי תתי קבוצות הוא ריק (\forall i\not= j\in I : A_i\cap A_j = \phi )

הגדרה:

יהא R יחס שקילות על A אזי

  1. לכל x\in A מוגדרת מחלקת השקילות של x להיות \bar{x}=[x]_R:=\{y\in A | (x,y)\in R\}
  2. קבוצת המנה מוגדרת A/R := \{ [x]_R | x\in A\}


למשל בדוגמא משבוע שעבר על השלמים עם היחס 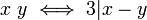x~y\iff 3|x-y, מחלקת השקילות של 0 היא [0]_R=\{ 0 \pm 3 \pm 6 \dots \} וקבוצת המנה היא \mathbb{Z}/R= \{[0]_R,[1]_R,[2]_R\} (כלומר כל השאריות האפשריות בחלוקה ב-3).


משפט: יהא R יחס שקילות על A אזי

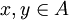  1. לכל x,y\in A מתקיים [x]=[y] או [x]\cap [y] =\phi (כלומר מחלקות השקילות זרות)
  2. A=\bigcup_{[x]\in A/R}[x] כלומר (איחוד מחלקות השקילות תתן את כל A)

הערה: זה בדיוק אומר שמיחס שקילות ניתן להגיע לחלוקה של A


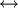מסקנה: תהא A קבוצה אזי יש התאמה {R יחס שקילות על A } \leftrightarrow {חלוקות של A}

חידוד: מהותו העיקרית של יחס שקילויות הוא לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת.

שאלה ממבחן

תהי A קבוצה לא ריקה ותהי 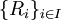\{R_i\}_{i\in I} משפחה של יחסי שקילות על A. הוכיחו כי החיתוך הכללי 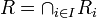R=\cap_{i\in I}R_i הינו יחס שקילויות על A.

פתרון

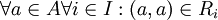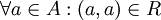רפלקסיביות: מאחר ו \forall a\in A\forall i\in I : (a,a)\in R_i נובע ש \forall a\in A: (a,a)\in R.

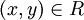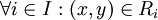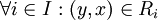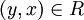סימטריות: נניח (x,y)\in R לכן \forall i\in I:(x,y)\in R_i ולכן נובע מסמטריות היחסים ש \forall i\in I:(y,x)\in R_i ולכן (y,x)\in R.

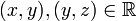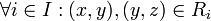טרנזיטיביות: נניח (x,y),(y,z)\in \mathbb R אזי \forall i\in I:(x,y),(y,z)\in R_i, וכיון שהוא יחס שקילות אז נובע 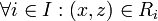\forall i\in I:(x,z)\in R_i, ולפי הגדרת החיתוך הכללי נקבל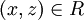 (x,z)\in R

תרגיל

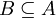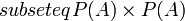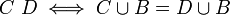תהא B\subseteq A קבוצה ותת קבוצה. נגדיר יחס ~subseteq P(A)\times P(A) ע"י C~D\iff C\cup B=D\cup B. הוכח שזהו יחס שקילות.

פיתרון

רפלקסיביות: כמובן ש-

מקור: https://math-wiki.com/index.php?title=תרגול_11_תשעז&oldid=69938