הבדלים בין גרסאות בדף "תרגול 13 תשעז"
(←הכנה למבחן) |
(←עוצמות) |
||
| שורה 18: | שורה 18: | ||
==עוצמות== | ==עוצמות== | ||
| − | בעבר ראינו את התרגיל הבא: תהא <math>B\subseteq A</math> קבוצה ותת קבוצה. נגדיר יחס <math>\sim \subseteq P(A)\times P(A)</math> ע"י <math>C\sim D\iff C\cap B=D\cap B</math>. ראינו שזהו יחס שקילות ונדרשנו למצוא את <math>|P(A)/\sim |</math>. וראינו: <math>|P(A)/\sim |=|P(B)|=2^{|B|}</math>. נשים לב שמה שעשינו אז היה בעצם | + | בעבר ראינו את התרגיל הבא: תהא <math>B\subseteq A</math> קבוצה ותת קבוצה. נגדיר יחס <math>\sim \subseteq P(A)\times P(A)</math> ע"י <math>C\sim D\iff C\cap B=D\cap B</math>. ראינו שזהו יחס שקילות ונדרשנו למצוא את <math>|P(A)/\sim |</math>. וראינו: <math>|P(A)/\sim |=|P(B)|=2^{|B|}</math>. נשים לב שמה שעשינו אז היה בעצם להראות שיש פונקציה חח"ע ועל בין הקבוצות, והיא <math>f:P(B) \rightarrow P(A)/\sim</math> המוגדרת ע"י <math>f(C)=[C]</math>. היא חח"ע כי לכל שתי קבוצות שונות מ-<math>B</math> יש מחלקות שקילות שונות כי הן אינן שקולות (החיתוך שלהן עם <math>B</math> זה הן עצמן, והן שונות). היא על, כי כפי שראינו לכל <math>[C]\in P(A)/\sim</math> מתקיים ש- <math>C\cap B\sim C\land C\cap B\in B</math>, ולכן <math>C\cap B</math> היא המקור. לכן יש להן אותה עוצמה. |
==הכנה למבחן== | ==הכנה למבחן== | ||
גרסה מ־09:18, 27 ביוני 2017
איזומורפיזמים בין קס"חים
תרגיל
האם 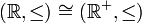 ?
?
פתרון
כן. נוכל להגדיר 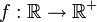 ע"י
ע"י 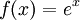 , והיא כמובן חח"ע ועל ושומרת סדר.
, והיא כמובן חח"ע ועל ושומרת סדר.
תרגיל
תהיינה 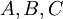 קס"ח כך ש
קס"ח כך ש 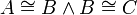 . הוכח או הפרך:
. הוכח או הפרך: 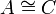 .
.
פתרון
הוכחה: יש פונקציות חח"ע, על ושומרות סדר 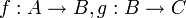 , ההרכבה שלהן
, ההרכבה שלהן 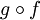 היא חח"ע ועל (משפט) והיא גם שומרת סדר.
היא חח"ע ועל (משפט) והיא גם שומרת סדר.
עוצמות
בעבר ראינו את התרגיל הבא: תהא 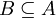 קבוצה ותת קבוצה. נגדיר יחס
קבוצה ותת קבוצה. נגדיר יחס 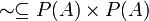 ע"י
ע"י 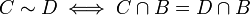 . ראינו שזהו יחס שקילות ונדרשנו למצוא את
. ראינו שזהו יחס שקילות ונדרשנו למצוא את 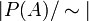 . וראינו:
. וראינו: 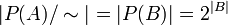 . נשים לב שמה שעשינו אז היה בעצם להראות שיש פונקציה חח"ע ועל בין הקבוצות, והיא
. נשים לב שמה שעשינו אז היה בעצם להראות שיש פונקציה חח"ע ועל בין הקבוצות, והיא 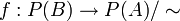 המוגדרת ע"י
המוגדרת ע"י ![f(C)=[C]](/images/math/2/9/1/2911ca042d1604588b414bfbafbc98e8.png) . היא חח"ע כי לכל שתי קבוצות שונות מ-
. היא חח"ע כי לכל שתי קבוצות שונות מ- יש מחלקות שקילות שונות כי הן אינן שקולות (החיתוך שלהן עם
יש מחלקות שקילות שונות כי הן אינן שקולות (החיתוך שלהן עם  זה הן עצמן, והן שונות). היא על, כי כפי שראינו לכל
זה הן עצמן, והן שונות). היא על, כי כפי שראינו לכל ![[C]\in P(A)/\sim](/images/math/3/1/d/31df71c1b549f0cd256293908a322f4d.png) מתקיים ש-
מתקיים ש- 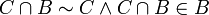 , ולכן
, ולכן 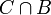 היא המקור. לכן יש להן אותה עוצמה.
היא המקור. לכן יש להן אותה עוצמה.
הכנה למבחן
תרגיל
תהיינה 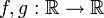 פונקציות. נאמר ש
פונקציות. נאמר ש מתאימה ל
מתאימה ל אם לכל
אם לכל 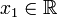 קיים
קיים 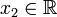 כך ש
כך ש 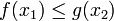 . הוכח או הפרך:
. הוכח או הפרך:
א. אם  מתאימה ל
מתאימה ל אז גם
אז גם  מתאימה ל
מתאימה ל .
.
ב. קיימת פונקציה  המתאימה לכל פונקציה
המתאימה לכל פונקציה  .
.
ג. קיימת פונקציה  שכל פונקציה
שכל פונקציה  מתאימה לה.
מתאימה לה.
ד. האם זהו יחס סדר חלקי?
פתרון
א. לא נכון. למשל ניקח שתי פונקציות קבועות שונות.
ב. לא. נניח בשלילה שיש  כזו. אז היא מתאימה לכל פונקציה קבועה
כזו. אז היא מתאימה לכל פונקציה קבועה 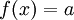 , ולכן לכל
, ולכן לכל 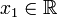 צריך להתקיים
צריך להתקיים 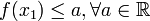 , וזה לא יכול להיות.
, וזה לא יכול להיות.
ג. נכון, למשל 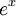 . כי תהי
. כי תהי 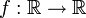 פונקציה ויהי
פונקציה ויהי 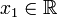 אזי מתקיים
אזי מתקיים 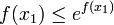 .
.
ד. לא הפונקציות 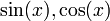 שונות ומאימות אחת לשניה. כלומר זה יחס שאיננו אנטי סימטרי.
שונות ומאימות אחת לשניה. כלומר זה יחס שאיננו אנטי סימטרי.