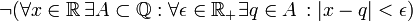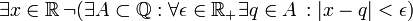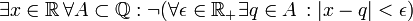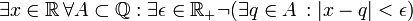תרגול 2 תשעז
חזרה לדף מערכי התרגול.
תוכן עניינים
כַּמָּתִים ופרדיקטים
פרדיקטים
בלוגיקה מתמטית, פרדיקט הוא פונקציה המקבלת משתנה או כמה משתנים, ומחזירה ערך אמת (T או F). זוהי הכללה של האטומים שפגשנו בתרגול הקודם, שאינם אלא פרדיקטים ללא משתנים. לדוגמה ניתן להגדיר את הפרדיקט 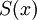 להיות "
להיות " הינו סטודנט באוניברסיטה".
הינו סטודנט באוניברסיטה".
גם אטומים וגם פרדיקטים יכולים להיות אמיתיים (מסמנים 1 או T) או שקריים (מסמנים 0 או F). המינוח המקובל הוא שאטום/פרדיקט הוא בעל ערך אמת T (במידה שהוא נכון) או בעל ערך אמת F (במידה שאינו נכון).
כיוון שאטומים הם ללא משתנים הם יכולים להיות T או F אבל לא שניהם. לעומתם, פרדיקטים הם תלויים במשתנים ולכן ערך האמת שלהם יקבע לפי ההצבה במשתנים. למשל הפרדיקט 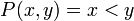 יהיה נכון במקרה ש
יהיה נכון במקרה ש 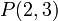 ולא נכון במקרה ש
ולא נכון במקרה ש 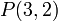 .
.
כמתים
בנוסף, לקשרים ניתן להוסיף כמתים (quantifiers). החשובים שבהם הם הכמת "לכל" 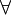 (זו A הפוכה, קיצור המילה All) והכמת "קיים"
(זו A הפוכה, קיצור המילה All) והכמת "קיים" 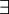 (זו E הפוכה, קיצור המילה Exist).
(זו E הפוכה, קיצור המילה Exist).
תפקיד מרכזי של הכמת הוא להבהיר את כוונת הטענה. למשל הטענה ש "סטונדט הוא יצור חרוץ" יכולה לקבל 2 משמעויות בעזרת הכמתים. או "כל סטודנט הוא יצור חרוץ" או "קיים סטודנט שהוא יצור חרוץ".
הטענה הראשונה טוענת לגבי כלל הסטודנטים (אם רוצים להוכיח כי הטענה נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם חרוצים ואם רוצים להוכיח כי הטענה לא נכונה מספיק למצוא סטודנט אחד שאינו חרוץ).
לעומתה הטענה השניה טוענת שניתן למצוא סטודנט אחד (לפחות) שהוא חרוץ (אם רוצים להוכיח את הטענה צריך למצוא סטודנט שהוא חרוץ ואם רוצים להוכיח כי הטענה לא נכונה צריך לעבור בין כל הסטודנטים ולוודא שהם אינם חרוצים).
תרגיל
הצרן: לכל מספר p גדול מ-1: (p ראשוני) אמ"מ (אם הוא מחלק מכפלת מספרים אז הוא מחלק את אחד המספרים).
פתרון:
ההצרנה 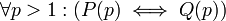 כאשר
כאשר
-
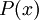 הוא הפרדיקט "
הוא הפרדיקט " הוא ראשוני".
הוא ראשוני". -
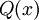 הוא הפרדיקט
הוא הפרדיקט 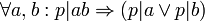
הערה: סדר הכמתים כן משנה (לפעמים) למשל 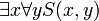 לא שקול לפסוק
לא שקול לפסוק 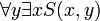 .
.
לדוגמא: יש הבדל בין "לכל סיר קיים מכסה" לבין "קיים מכסה שמתאים לכל סיר". האם אחד מן הפסוקים האלו גורר את השני?
עוד דוגמא: הצרן את המשפט "לכל מספר טבעי יש מספר טבעי הגדול ממנו" פתרון: 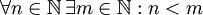 לעומת זאת
לעומת זאת 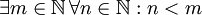 פירושו שקיים מספר טבעי שגדול מכל המספרים הטבעיים.
פירושו שקיים מספר טבעי שגדול מכל המספרים הטבעיים.
נשים לב כי בשביל לקבוע אם הפסוק 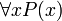 אנחנו צריכים לדעת איזה
אנחנו צריכים לדעת איזה  -ים "חוקיים" (בהנחה שאנחנו יודעים את
-ים "חוקיים" (בהנחה שאנחנו יודעים את 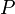 ).
).
סימון: נעיר שיש דרכים רבות לכתוב פסוקים כגון אלו. מקובל למשל 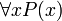 ,
, 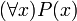 או
או 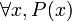 . כל הסגנונות חוקיים, בתנאי שהפסוק ניתן לקריאה באופן חד-משמעי.
. כל הסגנונות חוקיים, בתנאי שהפסוק ניתן לקריאה באופן חד-משמעי.
הערה: לכל כמת יש אזור תחולה. בתוך אזור תחולה שמות המשתנים אינם חשובים. למשל עבור הפרדיקט 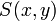 המוגדר
המוגדר 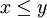 הפסוק
הפסוק 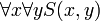 הוא זהה לפסוק
הוא זהה לפסוק 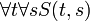 .
.
תרגיל
שימו לב שגם למשתנים בהגדרות יש אזור תחולה. צריך לשים לב לא להתבלבל באזורים האלו, וכדי למנוע "התנגשויות" בשמות, פשוט נחליף אותם. למשל נגדיר מספר  להיות דו־ריבועי אם קיימים
להיות דו־ריבועי אם קיימים 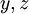 כך ש-
כך ש-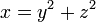 . הוכיחו שלכל זוג מספרים
. הוכיחו שלכל זוג מספרים 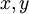 אם הם מספרים דו־ריבועיים, אז גם המספר
אם הם מספרים דו־ריבועיים, אז גם המספר 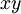 הוא דו־ריבועי.
הוא דו־ריבועי.
פתרון: נגדיר את הפרדיקט 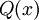 להיות T אם ורק אם
להיות T אם ורק אם  הוא מספר דו־ריבועי (הצרינו זאת!). אנו נדרשים להוכיח את הטענה
הוא מספר דו־ריבועי (הצרינו זאת!). אנו נדרשים להוכיח את הטענה 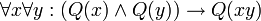 .
.
לפי ההגדרה, אם  הוא דו־ריבועי, אז קיימים
הוא דו־ריבועי, אז קיימים 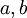 כך ש-
כך ש-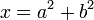 , ובאופן דומה אם
, ובאופן דומה אם  דו־ריבועי, אז קיימים
דו־ריבועי, אז קיימים 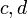 כך ש-
כך ש-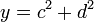 . כדי להוכיח ש-
. כדי להוכיח ש-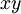 הוא גם דו־ריבועי, יש להראות שקיימים
הוא גם דו־ריבועי, יש להראות שקיימים 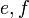 כך ש-
כך ש-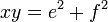 . נעזר בזהות
. נעזר בזהות 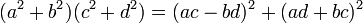 . לכן קיבלנו
. לכן קיבלנו 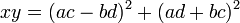 , ומכאן שנוכל לבחור את
, ומכאן שנוכל לבחור את 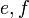 הדרושים לנו להיות
הדרושים לנו להיות 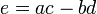 ,
, 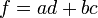 .
.
שלילת פסוקים
מהי השלילה של הפסוק "לכל סיר יש מכסה המתאים לו", או "לכל מאכל, יש מישהו שמכין אותו טעים"?
בעת שלילה של פסוק לוגי, הכמתים 'לכל' ו'קיים' מתחלפים זה עם זה, והשלילה עוברת הלאה. כלומר לכל פרדיקט 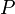 ,
,
-
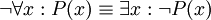 , וכך גם
, וכך גם -
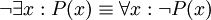 .
.
שלילה על הקשרים ניתן לבצע באמצעות טאוטולוגיות וטבלאות אמת.
תרגיל
הוכיחו או הפריכו:
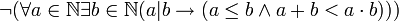
פיתרון: ראשית נראה מה הטענה בעצם אומרת:
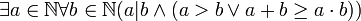
שימו לב שנעזרו בשקילות 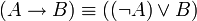 ובחוקי דה-מורגן. כעת נשים לב שאם
ובחוקי דה-מורגן. כעת נשים לב שאם 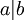 אז
אז 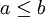 ולכן כדי שזה יהיה נכון צריך שיתקיים
ולכן כדי שזה יהיה נכון צריך שיתקיים 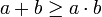 וזה אכן קורה עבור
וזה אכן קורה עבור 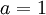 .
.
תרגיל
הוכח או הפרך (משתני הפרדיקט נלקחים מהטבעיים):
א. 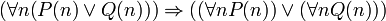
ב. 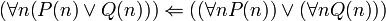
פיתרון:
א. הפרכה. ניקח את 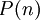 להיות
להיות 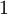 על הזוגיים ו-
על הזוגיים ו- על אי-זוגיים, ו-
על אי-זוגיים, ו-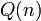 להפך. אכן כל מספר טבעי הוא זוגי או אי-זוגי, אך זה לא נכון שכל מספר הוא זוגי או שכל מספר הוא אי-זוגי.
להפך. אכן כל מספר טבעי הוא זוגי או אי-זוגי, אך זה לא נכון שכל מספר הוא זוגי או שכל מספר הוא אי-זוגי.
ב. הוכחה: יהי  . אם מתקיים
. אם מתקיים 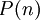 אז בפרט מתקיים
אז בפרט מתקיים 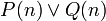 כדרוש. אחרת, לפי השקילות
כדרוש. אחרת, לפי השקילות 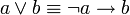 , מתקיים שלכל מס' טבעי, ובפרט עבור
, מתקיים שלכל מס' טבעי, ובפרט עבור  , מתקיים
, מתקיים 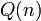 , ולכן מתקיים
, ולכן מתקיים 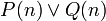 כדרוש.
כדרוש.
תרגיל
הצרן את המשפט "כל מספר ממשי ניתן לקרב ע"י מספרים רציונאליים בקירוב טוב כרצוננו".
פתרון: 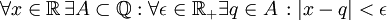 .
.
מה היא שלילתו של המשפט?
פתרון: נכתוב את השלילות השונות האפשריות:
תרגילים: דוגמאות של הצרנת ושלילת המושגים 'תלות לינארית', 'גבול סדרה', 'חח"ע', וכדומה