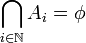הבדלים בין גרסאות בדף "תרגול 5 תשעז"
(←קבוצות) |
|||
| שורה 1: | שורה 1: | ||
==קבוצות== | ==קבוצות== | ||
| − | :הגדרה (לא מדוייקת): | + | :הגדרה (לא מדוייקת, אך מספיקה לצרכינו): |
'''קבוצה''' הינה אוסף של איברים שונים. בקבוצה אין משמעות לסדר האיברים, ואיבר אינו יכול להופיע פעמיים. דוגמאות ל3 קבוצות: | '''קבוצה''' הינה אוסף של איברים שונים. בקבוצה אין משמעות לסדר האיברים, ואיבר אינו יכול להופיע פעמיים. דוגמאות ל3 קבוצות: | ||
גרסה מ־08:04, 7 בדצמבר 2016
תוכן עניינים
קבוצות
- הגדרה (לא מדוייקת, אך מספיקה לצרכינו):
קבוצה הינה אוסף של איברים שונים. בקבוצה אין משמעות לסדר האיברים, ואיבר אינו יכול להופיע פעמיים. דוגמאות ל3 קבוצות:
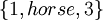 ,
, 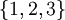 ו
ו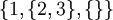
איבר השייך לקבוצה אנו מסמנים בסימן 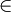 . למשל
. למשל 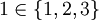 , ואילו
, ואילו 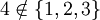 . שימו לב שגם
. שימו לב שגם 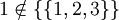 שכן האיבר היחיד בקבוצה זו הינה הקבוצה
שכן האיבר היחיד בקבוצה זו הינה הקבוצה 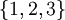 .
.
- אומרים שקבוצה A מוכלת בקבוצה B (מסומן
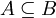 ) אם כל האיברים בA הם גם איברים בB. בשפה מדויקת, A מוכלת בB אם מתקיים
) אם כל האיברים בA הם גם איברים בB. בשפה מדויקת, A מוכלת בB אם מתקיים 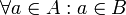 .
.
- דוגמא:
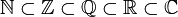 כאשר
כאשר
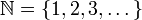 המספרים הטבעיים
המספרים הטבעיים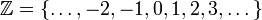 המספרים השלמים
המספרים השלמים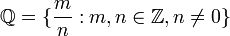 המספרים הרציונאלים (שברים)
המספרים הרציונאלים (שברים)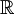 המספרים הממשיים ("כל המספרים" על הישר)
המספרים הממשיים ("כל המספרים" על הישר)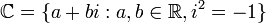 המספרים המרוכבים
המספרים המרוכבים
- חיתוך של שתי קבוצות A ו B הינו אוסף האיברים השייכים גם לA וגם לB (מסומן
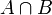 ). מתקיים ש
). מתקיים ש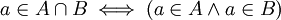 .
.
- איחוד של שתי קבוצות A ו B הינו אוסף האיברים השייכים לA או לB (מסומן
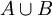 ). מתקיים ש
). מתקיים ש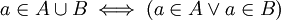 .
.
- קבוצות הן שוות אם הן מכילות את אותם האיברים. הדרך הנפוצה להוכיח שיוויון הינה הכלה דו כיוונית: A=B אם ורק אם
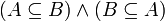 .
.
- A הפרש B הינה הקבוצה המכילה את כל האיברים בA שאינם בB (מסומן A\B). מתקיים ש
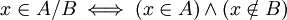 .
.
- ההפרש הסימטרי בין שתי קבוצות A וB הוא אוסף האיברים הנמצאים באחת הקבוצות אך לא בחיתוך (מסומן
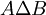 ). מתקיים ש
). מתקיים ש 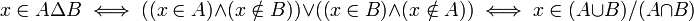
דוגמא:
יהיו 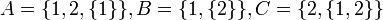 קבוצות.
קבוצות.
אזי:
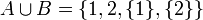
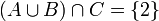
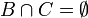
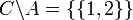
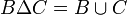
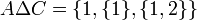
תכונות האיחוד והחיתוך (דומה לכפל וחיבור)
- אסוציאטיביות:
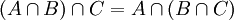 (וכנ"ל לגבי איחוד)
(וכנ"ל לגבי איחוד) - חילוף:
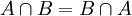 (וכנ"ל לגבי איחוד)
(וכנ"ל לגבי איחוד) - דיסטריביוטיביות:
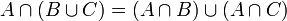 , וגם
, וגם 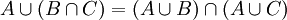
תרגיל
הוכח כי 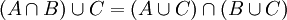 . במילים: האיברים שהם (גם בA וגם בB) או בC הם בדיוק האיברים ב(A או C) וגם ב(B או C)
. במילים: האיברים שהם (גם בA וגם בB) או בC הם בדיוק האיברים ב(A או C) וגם ב(B או C)
פתרון
נראה שקילות בין התנאים של איבר להיות באחת הקבוצות.
![x\in (A\cap B)\cup C \iff [x\in (A\cap B)] \or [x\in C] \iff [x\in A \and x\in B] \or [x\in C]](/images/math/5/a/4/5a46220a7b2be5a95beb3cbab300380a.png)
כעת, מתוך הטאוטולוגיה 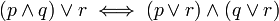 קל להשיג את השקילות למה שצריך.
(הערה: ניתן להשתכנע בקלות בטאוטולוגיה באופן הבא: אם r=1 אזי נשאר עם הטאוטולוגיה
קל להשיג את השקילות למה שצריך.
(הערה: ניתן להשתכנע בקלות בטאוטולוגיה באופן הבא: אם r=1 אזי נשאר עם הטאוטולוגיה
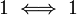 אם r=0 אזי נשאר עם הטאוטולוגיה
אם r=0 אזי נשאר עם הטאוטולוגיה
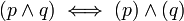 )
)
תרגיל
הוכח כי:
א. הקבוצה הריקה 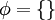 מוכלת בכל קבוצה A
מוכלת בכל קבוצה A
ב. 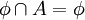
ג. 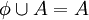
פתרון
א. יש להוכיח את הפסוק הבא: 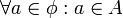 . אבל מכיוון שאין איברים בקבוצה הריקה, המשפט הזה נכון באופן ריק. זכרו ששקר גורר כל דבר, לכן האטום "איבר a שייך לקבוצה הריקה" גורר כל דבר.
הערה: שימו לב שעל מנת להוכיח שקבוצה A אינה מוכלת בקבוצה B, יש להראות כי קיים איבר בA שאינו שייך לB. אם היינו משתמשים בפסוק "כל האיברים בA אינם בB" היינו מקבלים שהקבוצה הריקה לא מוכלת בכל קבוצה, וגם אינה מוכלת בכל קבוצה.
. אבל מכיוון שאין איברים בקבוצה הריקה, המשפט הזה נכון באופן ריק. זכרו ששקר גורר כל דבר, לכן האטום "איבר a שייך לקבוצה הריקה" גורר כל דבר.
הערה: שימו לב שעל מנת להוכיח שקבוצה A אינה מוכלת בקבוצה B, יש להראות כי קיים איבר בA שאינו שייך לB. אם היינו משתמשים בפסוק "כל האיברים בA אינם בB" היינו מקבלים שהקבוצה הריקה לא מוכלת בכל קבוצה, וגם אינה מוכלת בכל קבוצה.
ב. 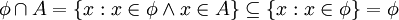
ג. 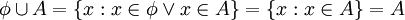
הכללה לאיחודים וחיתוכים כל שהם
מוטיבציה: הגדרנו את החיתוך והאיחוד עבור שתי קבוצות. לעיתים נרצה לחתוך או לאחד יותר קבוצות, לדוגמא נרצה לדבר על חיתוכן של 17 הקבוצות 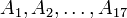 . מכיוון שחיתוך ואיחוד הן פעולות אסוציטיביות, ניתן לרשום
. מכיוון שחיתוך ואיחוד הן פעולות אסוציטיביות, ניתן לרשום 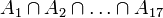 , וזה ביטוי חד משמעי. אך צורת רישום זו היא ארוכה, ולכן אנו מסמנים את החיתוך הזה בקיצור הבא:
, וזה ביטוי חד משמעי. אך צורת רישום זו היא ארוכה, ולכן אנו מסמנים את החיתוך הזה בקיצור הבא: 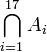 . לעיתים נרצה לחתוך או לאחד אוסף אינסופי של קבוצות, ולכך באה ההכללה הבאה:
. לעיתים נרצה לחתוך או לאחד אוסף אינסופי של קבוצות, ולכך באה ההכללה הבאה:
הגדרה:
יהיו 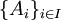 אוסף קבוצות כאשר
אוסף קבוצות כאשר 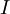 הוא קבוצת אינדקסים אזי נגדיר את האיחוד והחיתוך של אוסף הקבוצות כך:
הוא קבוצת אינדקסים אזי נגדיר את האיחוד והחיתוך של אוסף הקבוצות כך:
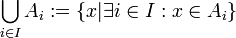
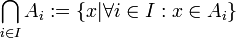 . כאן יש להניח שקבוצת האינדקסים
. כאן יש להניח שקבוצת האינדקסים 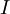 לא ריקה.
לא ריקה.
דוגמא:
נגדיר ![\forall n\in \mathbb{N} \; A_n:=[n,n+1]](/images/math/b/e/6/be669fb7637e3c1c6e6bd1431436da46.png) אזי
אזי