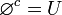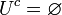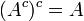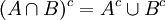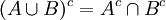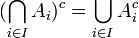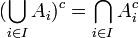תרגול 6 תשעז
חזרה לדף מערכי התרגול.
תוכן עניינים
המשך קבוצות
משלים
הגדרה: תהי קבוצה 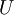 , ונביט בתת קבוצה שלה
, ונביט בתת קבוצה שלה  . ניתן להגדיר את המשלים של
. ניתן להגדיר את המשלים של  כאוסף האיברים ב-
כאוסף האיברים ב-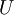 שאינם ב-
שאינם ב- (כלומר ההפרש
(כלומר ההפרש 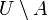 ), המסומן
), המסומן 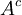 . לא ניתן לדבר על משלים אוניברסלי ללא
. לא ניתן לדבר על משלים אוניברסלי ללא 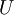 מכיוון שאין קבוצה המכילה את כל הדברים בעולם (אחרת נגיע לסתירות כמו פרדוקס ראסל).
מכיוון שאין קבוצה המכילה את כל הדברים בעולם (אחרת נגיע לסתירות כמו פרדוקס ראסל).
תכונות בסיסיות:
על המשלימים מתקיימים חוקי דה מורגן (הנובעים ישירות מחוקי דה מורגן בלוגיקה):
הערה: באופן כללי מתקיים
תרגיל
הוכיחו כי 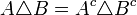 .
.
פתרון
נשתמש בהצגת ההפרש הסימטרי כאיחוד ההפרשים:
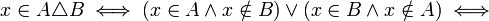
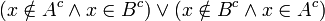 ומחילופיות "וגם" ו"או":
ומחילופיות "וגם" ו"או":
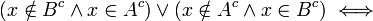
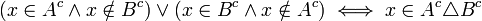
תרגיל
לכל 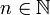 נגדיר
נגדיר 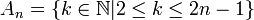 ונגדיר
ונגדיר 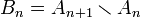 .
.
א. מצאו את 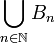 .
.
ב. נגדיר 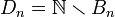 . מצאו את
. מצאו את 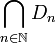 .
.
פתרון
א. התשובה: 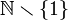 . הוכחה:
. הוכחה:
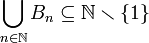 : הכל תת קבוצות של הטבעיים וכל הקבוצות מוגדרות ע"י איברים הגדולים מ-
: הכל תת קבוצות של הטבעיים וכל הקבוצות מוגדרות ע"י איברים הגדולים מ-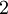 .
.
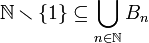 : יהי
: יהי 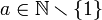 נמצא קבוצה בה הוא נמצא. נשים לב ש-
נמצא קבוצה בה הוא נמצא. נשים לב ש-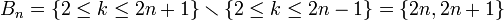 . לכן אם
. לכן אם  זוגי הוא נמצא ב-
זוגי הוא נמצא ב- 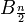 ואם אי-זוגי אז
ואם אי-זוגי אז 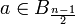 .
.
ב. נתייחס ל-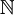 כקבוצה האוניברסלית לדיוננו. לפי דה-מורגן נקבל:
כקבוצה האוניברסלית לדיוננו. לפי דה-מורגן נקבל: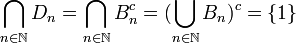 .
.
קבוצת החזקה
הגדרה: תהי קבוצה  . נגדיר את קבוצת החזקה של
. נגדיר את קבוצת החזקה של  בתור אוסף כל תת הקבוצות של
בתור אוסף כל תת הקבוצות של  . נסמן
. נסמן 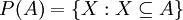 .
.
האם אתם יכולים למנות כמה איברים יש בקבוצת החזקה? הוכיחו זאת באינדוקציה.
תרגיל
הוכיחו או הפריכו: 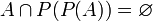 .
.
פתרון
הפרכה : ניקח 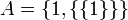 .
.
תרגיל
הוכיחו או הפריכו:
א. 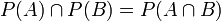
ב. 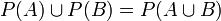
פתרון
א. הוכחה: 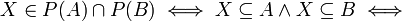
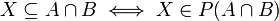
ב. הפרכה: ניקח 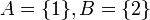 . אז
. אז 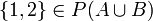 , אבל לא ל-
, אבל לא ל-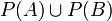 .
.
למעשה הוכיחו כי 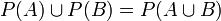 אם ורק אם
אם ורק אם 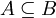 או
או 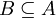 .
.
תרגיל ממבחן
תהינה 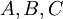 קבוצות. הוכיחו או הפריכו:
קבוצות. הוכיחו או הפריכו:
א. אם 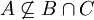 אזי
אזי 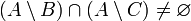
ב. אם 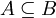 אזי
אזי 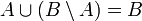
ג. אם 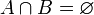 אזי
אזי 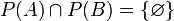
פתרון
א. הפרכה: 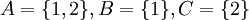 . אזי ברור ש-
. אזי ברור ש- איננה מוכלת בחיתוך
איננה מוכלת בחיתוך 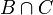 אבל
אבל 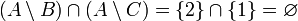 .
.
ב. נתון שלכל 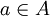 מתקיים
מתקיים 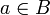 . אזי
. אזי
![x\in [A\cup(B\setminus A)] \iff (x\in A) \or [(x\in B)\and (x\notin A)] \iff](/images/math/6/d/e/6de9d6fa72f50a95b5c79563e301ac42.png)
![[(x\in A) \or (x\in B)] \and [(x \in A)\or (x\notin A)]](/images/math/b/6/7/b6778e92eee55248e0d924f48638dc11.png)
כעת, הצד הימני הוא טאוטולוגיה וניתן להסיר אותו. מכיוון שנתון  ניתן להסיק בקלות ש-
ניתן להסיק בקלות ש-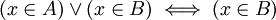 , כפי שרצינו.
, כפי שרצינו.
דרך נוספת: נגדיר את  להיות הקבוצה האוניברסאלית
להיות הקבוצה האוניברסאלית 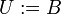 ואז צריך להוכיח כי
ואז צריך להוכיח כי
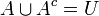 וזה אכן נכון!
וזה אכן נכון!
ג. נניח בשלילה ש-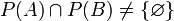 . מכיוון שהקבוצה הריקה שייכת לכל קבוצת חזקה, החיתוך אינו ריק. לכן לפי הנחת השלילה קיימת קבוצה לא ריקה
. מכיוון שהקבוצה הריקה שייכת לכל קבוצת חזקה, החיתוך אינו ריק. לכן לפי הנחת השלילה קיימת קבוצה לא ריקה 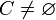 השייכת לחיתוך
השייכת לחיתוך 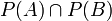 . קבוצות החזקה הן אוסף תת הקבוצות, ולכן
. קבוצות החזקה הן אוסף תת הקבוצות, ולכן 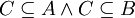 . מכיוון ש-
. מכיוון ש-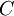 אינה ריקה קיים בה איבר
אינה ריקה קיים בה איבר 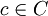 וקל לראות ש-
וקל לראות ש-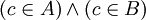 ולכן
ולכן 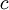 מוכל בחיתוך, בסתירה לכך שהחיתוך ריק.
מוכל בחיתוך, בסתירה לכך שהחיתוך ריק.