הבדלים בין גרסאות בדף "תרגול 8 תשעז"
(←תכונות של יחסים על קבוצה) |
(←פתרון) |
||
| (3 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | חזרה ל[[83-116, בדידה 1 להנדסה, מערכי תרגול|דף מערכי התרגול]]. | ||
| + | |||
=יחסים= | =יחסים= | ||
==המכפלה הקרטזית== | ==המכפלה הקרטזית== | ||
| − | הגדרה: '''המכפלה הקרטזית''' של שתי קבוצות A | + | הגדרה: '''המכפלה הקרטזית''' של שתי קבוצות <math>A</math> ו-<math>B</math> הינה אוסף כל ה'''זוגות הסדורים''' - <math>A\times B = \{(a,b)|a\in A \and b\in B\}</math>. ההבדל בין זוג סדור לבין קבוצה המכילה זוג איברים היא שהאיברים יכולים להיות שווים בזוג סדור, והסדר שלהם מהותי. כלומר שני האיברים הבאים שונים <math>(1,2),(2,1)</math> והאיבר הבא הינו זוג חוקי <math>(1,1)</math>. |
| − | ניתן להכליל את ההגדרה לעיל | + | ניתן להכליל את ההגדרה לעיל ל-<math>n</math>-יה סדורה - כלומר <math>n</math> איברים מסודרים. |
| − | + | דוגמה: <math>A=\{1,2,3\}</math> ו-<math>B=\{a,b\}</math> אזי מתקיים <math>A\times B =\{(1,a),(2,a),(3,a),(1,b),(2,b),(3,b)\}</math> | |
| + | למתכנתים: זה מאוד דומה ללולאות for מקוננות. | ||
===תרגיל=== | ===תרגיל=== | ||
| − | הוכח שלכל קבוצות A,B,C,D מתקיים <math>(A\times B)\cap (C\times D)=(A\cap C)\times (B\cap D)</math> | + | הוכח שלכל קבוצות <math>A,B,C,D</math> מתקיים <math>(A\times B)\cap (C\times D)=(A\cap C)\times (B\cap D)</math> |
====פתרון==== | ====פתרון==== | ||
| − | <math>(x,y)\in (A\times B)\cap (C\times D) \iff (x,y)\in A\times B \land (x,y)\in C\times D \iff (x\in A \and y\in B) \and (x\in C\and y\in D) \iff (x\in A\and x\in C) \and (y\in B\and y\in D) \iff (x,y)\in (A\cap C)\times (B\cap D)</math> | + | <math>(x,y)\in (A\times B)\cap (C\times D) \iff </math> |
| + | |||
| + | <math>(x,y)\in A\times B \land (x,y)\in C\times D \iff</math> | ||
| + | |||
| + | <math>(x\in A \and y\in B) \and (x\in C\and y\in D) \iff</math> | ||
| + | |||
| + | <math>(x\in A\and x\in C) \and (y\in B\and y\in D) \iff</math> | ||
| + | |||
| + | <math>(x,y)\in (A\cap C)\times (B\cap D)</math> | ||
==יחסים כתת קבוצה של הזוגות הסדורים== | ==יחסים כתת קבוצה של הזוגות הסדורים== | ||
| − | הגדרה: יהיו A,B קבוצות, <math>R\subseteq A\times B</math> אזי R יקרא יחס (בין A | + | הגדרה: יהיו <math>A,B</math> קבוצות, <math>R\subseteq A\times B</math> אזי <math>R</math> יקרא יחס (בין <math>A</math> לבין <math>B</math>). |
| − | הרעיון שעומד בבסיסו של יחס הוא האפשרות "להשוות" בין איברי | + | הרעיון שעומד בבסיסו של יחס הוא האפשרות "להשוות" בין איברי <math>A</math> ל-<math>B</math>. |
| − | + | ||
| − | + | דוגמה: <math>A=\{1,2,3\},B=\{0,2,6\}</math> ונביט בתת הקבוצה <math>R\subseteq A\times B</math> הבאה: <math>R=\{(1,2),(1,6),(2,2),(2,6),(3,6)\}</math>. מה מיוחד בזוגות אלה? | |
| − | + | זוגות אלה הינם כל זוגות האיברים <math>(a,b)</math> כך ש-<math>a\leq b</math>. (כלומר הגדרנו את היחס המייצג "קטן שווה"). | |
| − | + | הערה: יחס לא חייב לייצג חוקיות מסוימת למשל גם הקבוצה <math>S=\{(1,2),(1,6),(2,0),(2,2)\}</math> היא יחס. גם <math>\varnothing</math> היא יחס, וגם <math>A\times B</math> הוא יחס. | |
| + | סימון: אם זוג מסוים,נניח <math>(a,b)</math>, נמצא בקבוצת היחס <math>R</math> נהוג לסמן <math>aRb</math>, או <math>(a,b)\in R</math>. (אם יש משמעות ליחס כמו לעיל ניתן גם לסמן פשוט <math>a\leq b</math>). | ||
| − | + | דוגמה: נביט בקבוצת האנשים <math>A</math>. נגדיר את יחס "בן של" על ידי קבוצת הזוגות הסדורים <math>R\subseteq A\times A</math> כך ש-<math>(x,y)\in R</math> אם"ם <math>x</math> הוא בן של <math>y</math>. שימו לב שיש משמעות לכיוון היחס, שכן יש הבדל בין העובדה שאני הבן של מישהו לבין העובדה שהוא הבן שלי. | |
| − | הגדרה: בהינתן יחס <math>R\subseteq A\times B</math> '''היחס ההפוך''' <math>R^{-1}\subseteq B\times A</math> הוא היחס המוגדר ע"י היפוך הזוגות הסדורים: | + | הגדרה: בהינתן יחס <math>R\subseteq A\times B</math>, '''היחס ההפוך''' <math>R^{-1}\subseteq B\times A</math> הוא היחס המוגדר ע"י היפוך הזוגות הסדורים: |
<math>R^{-1}=\{(b,a):aRb\}</math> | <math>R^{-1}=\{(b,a):aRb\}</math> | ||
| − | הגדרה: תהי קבוצה A. '''יחס הזהות''' הוא <math>R\subseteq A\times A</math> כך ש | + | הגדרה: תהי קבוצה <math>A</math>. '''יחס הזהות''' על <math>A</math> הוא <math>R\subseteq A\times A</math> כך ש-<math>I_A=R=\{(a,a):a\in A\}</math>. |
| − | הגדרה: יהיו A,B,C קבוצות, ו<math>R\subseteq A\times B, S\subseteq B\times C</math> ''' | + | הגדרה: יהיו <math>A,B,C</math> קבוצות, ו-<math>R\subseteq A\times B, S\subseteq B\times C</math> '''יחס הכפל''' הוא היחס: <math>RS=\{(a,c)\in A\times C | \exists b\in B : (a,b)\in R \land (b,c)\in S\}</math>. |
===תרגיל=== | ===תרגיל=== | ||
יהיו <math>A=\{1,2\}, B=\{3,4,5\}</math>. נגדיר את היחס: <math>R=\{(1,3),(2,4)\}</math>. בדוק האם: | יהיו <math>A=\{1,2\}, B=\{3,4,5\}</math>. נגדיר את היחס: <math>R=\{(1,3),(2,4)\}</math>. בדוק האם: | ||
| − | א. <math> | + | א. <math>RR^{-1}=I_A</math> |
| − | ב. <math> | + | ב. <math>R^{-1}R=I_B</math> |
==תכונות של יחסים על קבוצה== | ==תכונות של יחסים על קבוצה== | ||
| − | הגדרה: יחס R על קבוצה A פירושו | + | הגדרה: יחס <math>R</math> על קבוצה <math>A</math> פירושו <math>R\subseteq A\times A</math>. |
| − | תהי קבוצה A ויחס R עליה אזי | + | תהי קבוצה <math>A</math> ויחס <math>R</math> עליה אזי: |
| − | #R נקרא '''רפלקסיבי''' אם כל איבר מקיים את היחס עם עצמו ( מתקיים <math>\forall a\in A:(a,a)\in R</math>) | + | #<math>R</math> נקרא '''רפלקסיבי''' אם כל איבר מקיים את היחס עם עצמו ( מתקיים <math>\forall a\in A:(a,a)\in R</math>). |
| − | #R נקרא '''סימטרי''' אם aRb גורר שגם bRa (מתקיים <math>\forall a,b\in A:[(a,b)\in R \rightarrow (b,a)\in R]</math>) | + | #<math>R</math> נקרא '''סימטרי''' אם <math>aRb</math> גורר שגם <math>bRa</math> (מתקיים <math>\forall a,b\in A:[(a,b)\in R \rightarrow (b,a)\in R]</math>). |
| − | #R נקרא '''טרנזיטיבי''' אם יחס בין ראשון לשני, ויחס בין השני לשלישי גורר יחס בין הראשון לשלישי (מתקיים <math>\forall a,b,c\in A:[((a,b)\in R) \and ((b,c)\in R) \rightarrow ((a,c)\in R)]</math>) | + | #<math>R</math> נקרא '''טרנזיטיבי''' אם יחס בין ראשון לשני (<math>aRb</math>), ויחס בין השני לשלישי (<math>bRc</math>) גורר יחס בין הראשון לשלישי (<math>aRc</math>). (מתקיים <math>\forall a,b,c\in A:[((a,b)\in R) \and ((b,c)\in R) \rightarrow ((a,c)\in R)]</math>). |
| − | #R נקרא '''אנטי סימטרי (חלש)''' אם aRb וגם bRa גורר כי a=b (מתקיים <math>\forall a,b\in A:[(a,b)\in R \and (b,a)\in R \rightarrow a=b]</math> ובאופן שקול: <math>\forall a\neq b\in A: \lnot (aRb\land bRa)</math>) | + | #<math>R</math> נקרא '''אנטי סימטרי (חלש)''' אם <math>aRb</math> וגם <math>bRa</math> גורר כי <math>a=b</math> (מתקיים <math>\forall a,b\in A:[(a,b)\in R \and (b,a)\in R \rightarrow a=b]</math> ובאופן שקול: <math>\forall a\neq b\in A: \lnot (aRb\land bRa)</math>) |
דוגמאות: | דוגמאות: | ||
| שורה 55: | שורה 66: | ||
*יחס 'קטן שווה' הינו רפלקסיבי, טרנזיטיבי ואנטי סימטרי | *יחס 'קטן שווה' הינו רפלקסיבי, טרנזיטיבי ואנטי סימטרי | ||
*יחס 'קטן ממש' הינו טרנזיטיבי ואנטי-סימטרי | *יחס 'קטן ממש' הינו טרנזיטיבי ואנטי-סימטרי | ||
| − | *יחס 'שיוויון מודולו n' הינו רפלקסיבי, סימטרי וטרנזיטיבי | + | *יחס 'שיוויון מודולו <math>n</math>' הינו רפלקסיבי, סימטרי וטרנזיטיבי |
*יחס 'הכלה' הינו רפלקסיבי, טרנזיטיבי ואנטי-סימטרי | *יחס 'הכלה' הינו רפלקסיבי, טרנזיטיבי ואנטי-סימטרי | ||
| − | *יחס 'a מחלק את b' הינו רפלקסיבי וטרנזיטיבי | + | *יחס '<math>a</math> מחלק את <math>b</math>' הינו רפלקסיבי וטרנזיטיבי |
| − | *יחס 'אדם x שמע על אדם y' הינו רפלקסיבי | + | *יחס 'אדם <math>x</math> שמע על אדם <math>y</math>' הינו רפלקסיבי |
| − | '''הערה:''' יחס יכול להיות גם סימטרי וגם אנטי סימטרי. וכמו כן הוא יכול להיות לא זה ולא זה! | + | '''הערה:''' יחס יכול להיות גם סימטרי וגם אנטי סימטרי. וכמו כן הוא יכול להיות לא זה ולא זה! לדוגמה: <math>A=\{ 1,2,3\} , R=\{ (1,1)\} , S=\{ (1,2),(2,1),(3,2)\}</math> ואז <math>R</math> גם וגם, ואילו <math>S</math> לא ולא. |
גרסה אחרונה מ־17:04, 5 בדצמבר 2017
חזרה לדף מערכי התרגול.
תוכן עניינים
יחסים
המכפלה הקרטזית
הגדרה: המכפלה הקרטזית של שתי קבוצות  ו-
ו- הינה אוסף כל הזוגות הסדורים -
הינה אוסף כל הזוגות הסדורים - 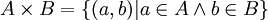 . ההבדל בין זוג סדור לבין קבוצה המכילה זוג איברים היא שהאיברים יכולים להיות שווים בזוג סדור, והסדר שלהם מהותי. כלומר שני האיברים הבאים שונים
. ההבדל בין זוג סדור לבין קבוצה המכילה זוג איברים היא שהאיברים יכולים להיות שווים בזוג סדור, והסדר שלהם מהותי. כלומר שני האיברים הבאים שונים 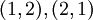 והאיבר הבא הינו זוג חוקי
והאיבר הבא הינו זוג חוקי 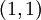 .
.
ניתן להכליל את ההגדרה לעיל ל- -יה סדורה - כלומר
-יה סדורה - כלומר  איברים מסודרים.
איברים מסודרים.
דוגמה: 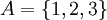 ו-
ו-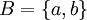 אזי מתקיים
אזי מתקיים 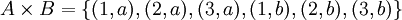
למתכנתים: זה מאוד דומה ללולאות for מקוננות.
תרגיל
הוכח שלכל קבוצות 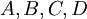 מתקיים
מתקיים 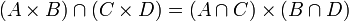
פתרון
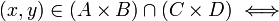
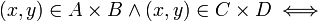
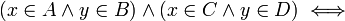
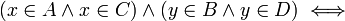
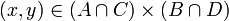
יחסים כתת קבוצה של הזוגות הסדורים
הגדרה: יהיו 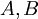 קבוצות,
קבוצות, 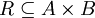 אזי
אזי  יקרא יחס (בין
יקרא יחס (בין  לבין
לבין  ).
הרעיון שעומד בבסיסו של יחס הוא האפשרות "להשוות" בין איברי
).
הרעיון שעומד בבסיסו של יחס הוא האפשרות "להשוות" בין איברי  ל-
ל- .
.
דוגמה: 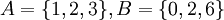 ונביט בתת הקבוצה
ונביט בתת הקבוצה 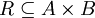 הבאה:
הבאה: 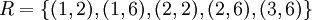 . מה מיוחד בזוגות אלה?
. מה מיוחד בזוגות אלה?
זוגות אלה הינם כל זוגות האיברים 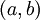 כך ש-
כך ש-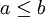 . (כלומר הגדרנו את היחס המייצג "קטן שווה").
. (כלומר הגדרנו את היחס המייצג "קטן שווה").
הערה: יחס לא חייב לייצג חוקיות מסוימת למשל גם הקבוצה 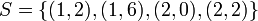 היא יחס. גם
היא יחס. גם 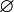 היא יחס, וגם
היא יחס, וגם 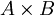 הוא יחס.
הוא יחס.
סימון: אם זוג מסוים,נניח 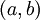 , נמצא בקבוצת היחס
, נמצא בקבוצת היחס  נהוג לסמן
נהוג לסמן 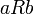 , או
, או 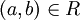 . (אם יש משמעות ליחס כמו לעיל ניתן גם לסמן פשוט
. (אם יש משמעות ליחס כמו לעיל ניתן גם לסמן פשוט 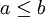 ).
).
דוגמה: נביט בקבוצת האנשים  . נגדיר את יחס "בן של" על ידי קבוצת הזוגות הסדורים
. נגדיר את יחס "בן של" על ידי קבוצת הזוגות הסדורים 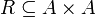 כך ש-
כך ש-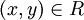 אם"ם
אם"ם  הוא בן של
הוא בן של  . שימו לב שיש משמעות לכיוון היחס, שכן יש הבדל בין העובדה שאני הבן של מישהו לבין העובדה שהוא הבן שלי.
. שימו לב שיש משמעות לכיוון היחס, שכן יש הבדל בין העובדה שאני הבן של מישהו לבין העובדה שהוא הבן שלי.
הגדרה: בהינתן יחס 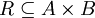 , היחס ההפוך
, היחס ההפוך 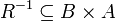 הוא היחס המוגדר ע"י היפוך הזוגות הסדורים:
הוא היחס המוגדר ע"י היפוך הזוגות הסדורים:
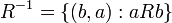
הגדרה: תהי קבוצה  . יחס הזהות על
. יחס הזהות על  הוא
הוא 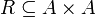 כך ש-
כך ש-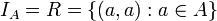 .
.
הגדרה: יהיו 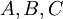 קבוצות, ו-
קבוצות, ו-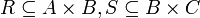 יחס הכפל הוא היחס:
יחס הכפל הוא היחס: 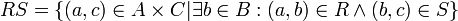 .
.
תרגיל
יהיו 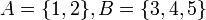 . נגדיר את היחס:
. נגדיר את היחס: 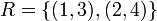 . בדוק האם:
. בדוק האם:
א. 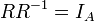
ב. 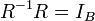
תכונות של יחסים על קבוצה
הגדרה: יחס  על קבוצה
על קבוצה  פירושו
פירושו 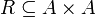 .
.
תהי קבוצה  ויחס
ויחס  עליה אזי:
עליה אזי:
 נקרא רפלקסיבי אם כל איבר מקיים את היחס עם עצמו ( מתקיים
נקרא רפלקסיבי אם כל איבר מקיים את היחס עם עצמו ( מתקיים 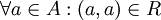 ).
). נקרא סימטרי אם
נקרא סימטרי אם 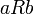 גורר שגם
גורר שגם 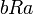 (מתקיים
(מתקיים ![\forall a,b\in A:[(a,b)\in R \rightarrow (b,a)\in R]](/images/math/e/3/6/e369a29b5080ca819f0a865d5e33d64f.png) ).
). נקרא טרנזיטיבי אם יחס בין ראשון לשני (
נקרא טרנזיטיבי אם יחס בין ראשון לשני (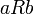 ), ויחס בין השני לשלישי (
), ויחס בין השני לשלישי (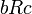 ) גורר יחס בין הראשון לשלישי (
) גורר יחס בין הראשון לשלישי (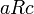 ). (מתקיים
). (מתקיים ![\forall a,b,c\in A:[((a,b)\in R) \and ((b,c)\in R) \rightarrow ((a,c)\in R)]](/images/math/3/b/1/3b121b7a1bf2a808e7435d6180f38fa6.png) ).
). נקרא אנטי סימטרי (חלש) אם
נקרא אנטי סימטרי (חלש) אם 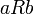 וגם
וגם 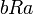 גורר כי
גורר כי 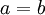 (מתקיים
(מתקיים ![\forall a,b\in A:[(a,b)\in R \and (b,a)\in R \rightarrow a=b]](/images/math/d/e/b/deb35f62640588ed122554bae3f23ced.png) ובאופן שקול:
ובאופן שקול: 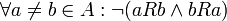 )
)
דוגמאות:
- יחס 'שיוויון' הינו רפלקסיבי, סימטרי וטרנזיטיבי
- יחס 'קטן שווה' הינו רפלקסיבי, טרנזיטיבי ואנטי סימטרי
- יחס 'קטן ממש' הינו טרנזיטיבי ואנטי-סימטרי
- יחס 'שיוויון מודולו
 ' הינו רפלקסיבי, סימטרי וטרנזיטיבי
' הינו רפלקסיבי, סימטרי וטרנזיטיבי - יחס 'הכלה' הינו רפלקסיבי, טרנזיטיבי ואנטי-סימטרי
- יחס '
 מחלק את
מחלק את 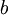 ' הינו רפלקסיבי וטרנזיטיבי
' הינו רפלקסיבי וטרנזיטיבי - יחס 'אדם
 שמע על אדם
שמע על אדם  ' הינו רפלקסיבי
' הינו רפלקסיבי
הערה: יחס יכול להיות גם סימטרי וגם אנטי סימטרי. וכמו כן הוא יכול להיות לא זה ולא זה! לדוגמה: 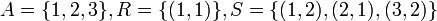 ואז
ואז  גם וגם, ואילו
גם וגם, ואילו 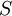 לא ולא.
לא ולא.