תרגול 9 תשעז
חזרה לדף מערכי התרגול.
תוכן עניינים
יחסי סדר
הגדרה: יחס  על קבוצה
על קבוצה  נקרא יחס סדר חלקי אם
נקרא יחס סדר חלקי אם  רפלקסיבי, טרנזיטיבי ואנטי-סימטרי.
רפלקסיבי, טרנזיטיבי ואנטי-סימטרי.
דוגמאות ליחסי סדר חלקי:
- היחס 'קטן-שווה' על המספרים השלמים
- היחס 'מוכל-שווה' על קבוצת החזקה
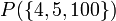
- היחס 'מחלק את' על הטבעיים
הערה:
עבור  קבוצה ויחס סדר חלקי
קבוצה ויחס סדר חלקי 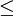 עליה, נסמן
עליה, נסמן 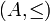 את הקבוצה עם היחס.
את הקבוצה עם היחס.
הגדרה: דיאגרמת הסה (או תרשים הסה, Hasse diagram) הינה דיאגרמה של יחס סדר חלקי על קבוצה. כל איבר  מחובר בקשת לאיבר
מחובר בקשת לאיבר  מתחתיו 'גדול' ממנו ביחס (כלומר
מתחתיו 'גדול' ממנו ביחס (כלומר 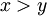 ), ובינם אין עוד איברים (כלומר אין
), ובינם אין עוד איברים (כלומר אין 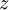 כך ש-
כך ש-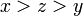 ). נצייר את דיאגרמת הסה ליחס הכלה על קבוצת החזקה של הקבוצה
). נצייר את דיאגרמת הסה ליחס הכלה על קבוצת החזקה של הקבוצה 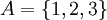 .
.
הגדרות: יהיו  קבוצה ו-
קבוצה ו- יחס סדר חלקי על הקבוצה:
יחס סדר חלקי על הקבוצה:
- איבר
 נקרא מינימלי ביחס ל-
נקרא מינימלי ביחס ל- אם
אם 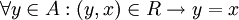 . כלומר, אין איבר 'קטן' מ-
. כלומר, אין איבר 'קטן' מ- . לא חייב להתקיים ש-
. לא חייב להתקיים ש- ביחס כלשהו עם איבר כלשהו.
ביחס כלשהו עם איבר כלשהו. - איבר
 נקרא מקסימלי ביחס ל-
נקרא מקסימלי ביחס ל- אם
אם 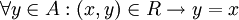 . כלומר, אין איבר 'גדול' מ-
. כלומר, אין איבר 'גדול' מ- . לא חייב להתקיים ש-
. לא חייב להתקיים ש- ביחס כלשהו עם איבר כלשהו.
ביחס כלשהו עם איבר כלשהו. - איבר
 נקרא קטן ביותר ביחס ל-
נקרא קטן ביותר ביחס ל- אם
אם 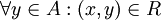 . כלומר,
. כלומר,  'קטן' מכל האיברים.
'קטן' מכל האיברים.  חייב להיות ביחס עם כל האיברים בקבוצה. למשל, הקבוצה הריקה תחת יחס הכלה.
חייב להיות ביחס עם כל האיברים בקבוצה. למשל, הקבוצה הריקה תחת יחס הכלה. - איבר
 נקרא גדול ביותר ביחס ל-
נקרא גדול ביותר ביחס ל- אם
אם 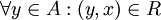 . כלומר,
. כלומר,  'גדול' מכל האיברים.
'גדול' מכל האיברים.  חייב להיות ביחס עם כל האיברים בקבוצה. למשל, הקבוצה
חייב להיות ביחס עם כל האיברים בקבוצה. למשל, הקבוצה  תחת יחס ההכלה על קבוצת החזקה של
תחת יחס ההכלה על קבוצת החזקה של  .
.
הערה: קל להוכיח מתוך תכונת האנטי-סימטריות שאם קיים איבר קטן ביותר הוא יחיד (למרות שהוא לא חייב להיות קיים), ונכון הדבר גם לגבי איבר גדול ביותר.
הערה: קטן ביותר גורר מינימלי, וכן גדול ביותר גורר מקסימלי. אבל לא להיפך!
צייר את דיאגרמת הסה של היחס "מחלק את" על הקבוצה 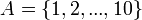 מהם האיברים המינימליים והמקסימליים? האם קיים איבר קטן ביותר ואיבר גדול ביותר?
צייר את היחס ההפוך של "מחלק את", זהו היחס "מתחלק ב". מהם האיברים המינימליים והמקסימליים? האם קיים איבר קטן ביותר ואיבר גדול ביותר?
מהם האיברים המינימליים והמקסימליים? האם קיים איבר קטן ביותר ואיבר גדול ביותר?
צייר את היחס ההפוך של "מחלק את", זהו היחס "מתחלק ב". מהם האיברים המינימליים והמקסימליים? האם קיים איבר קטן ביותר ואיבר גדול ביותר?
תרגיל
תהא  קבוצה. מצא את הקבוצה
קבוצה. מצא את הקבוצה 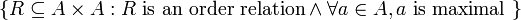
פתרון
נראה שיש רק יחס אחד כזה, והוא הזהות. יחס הזהות אכן מקיים את התנאי. נניח ש- יחס סדר המקיים את התנאי ונראה ש-
יחס סדר המקיים את התנאי ונראה ש-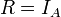 :
:
כיוון ראשון: כל יחס סדר  מקיים
מקיים 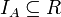 .
.
כיוון שני: יהי 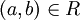 , אזי כיון ש-
, אזי כיון ש- מקסימלי נובע
מקסימלי נובע 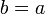 ולכן
ולכן 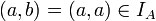 כדרוש.
כדרוש.
תרגיל
הוכח שאם  יחס סדר חלקי, אז גם היחס ההופכי שלו
יחס סדר חלקי, אז גם היחס ההופכי שלו 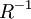 יחס סדר חלקי.
יחס סדר חלקי.
פתרון
- רפלקסיביות: לכל איבר
 מתקיים
מתקיים 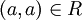 ולכן
ולכן 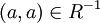 .
. - טרנזיטיביות: נניח
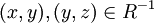 לכן מתקיים
לכן מתקיים 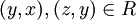 לכן לפי הטרנזיטיביות של R מתקיים
לכן לפי הטרנזיטיביות של R מתקיים 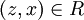 ולכן
ולכן 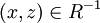 .
. - אנטי-סימטריות: אם
 ביחס ל-
ביחס ל- וגם
וגם  ביחס ל-
ביחס ל- הדבר נכון באופן זהה ל-
הדבר נכון באופן זהה ל- וליחס ההופכי שלו (כי 'וגם' חילופי), ולכן
וליחס ההופכי שלו (כי 'וגם' חילופי), ולכן  .
.
הגדרה: יהי  יחס סדר חלקי על
יחס סדר חלקי על  . אם לכל שני איברים
. אם לכל שני איברים 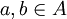 מתקיים
מתקיים ![[(a,b)\in R]\or[(b,a)\in R]](/images/math/1/d/4/1d4d3394750a0b97771353ed8775b927.png) אזי
אזי  נקרא יחס סדר מלא.
נקרא יחס סדר מלא.
דוגמה: היחס 'קטן שווה' על השלמים/הממשיים הוא יחס סדר מלא. שימו לב כי זו דוגמה ליחס סדר בלי איברים מינימליים או מקסימליים.
דוגמא ליחס סדר מעניין
היחס המילוני.
תרגיל
הוכיחו שאם  יחס סדר מלא על
יחס סדר מלא על  , ו-
, ו- 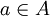 איבר מינימלי יחיד אז הוא גם קטן ביותר.
איבר מינימלי יחיד אז הוא גם קטן ביותר.
חסמים (בד"כ לא מלמדים בהנדסה)
הגדרות. יהיו  קבוצה,
קבוצה, 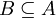 תת קבוצה המוכלת בה ו-
תת קבוצה המוכלת בה ו- יחס סדר חלקי:
יחס סדר חלקי:
- חסם מלעיל של
 הוא איבר
הוא איבר  כך שמתקיים
כך שמתקיים 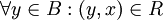
- חסם מלרע של B הוא איבר
 כך שמתקיים
כך שמתקיים 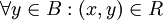
- החסם העליון (סופרמום) של
 הינו המינימום של קבוצת חסמי המלעיל (אם קיים). מסומן
הינו המינימום של קבוצת חסמי המלעיל (אם קיים). מסומן 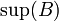
- החסם התחתון (אינפימום) של
 הינו המקסימום של קבוצת חסמי המלרע (אם קיים). מסומן
הינו המקסימום של קבוצת חסמי המלרע (אם קיים). מסומן 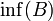
דוגמאות
דוגמה:
עבור 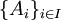 אוסף קבוצות. החסם העליון שלה הוא (ביחס להכלה) הוא
אוסף קבוצות. החסם העליון שלה הוא (ביחס להכלה) הוא
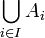 .
.
דוגמה:
נביט בקבוצה 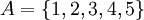 ונגדיר עליה יחס סדר חלקי:
ונגדיר עליה יחס סדר חלקי:
עיבוד הנוסחה נכשל (שגיאת תחביר): R=\{(1,1),(2,2),(3,3),(4,4),(5,5),\\(2,4),(1,2),(1,4),(3,2),(3,4),(5,2),(5,4)\}
(הזוגיים 'גדולים' מכל אי הזוגיים ומהזוגיים הקטנים מהם)
נביט בתת הקבוצה המכילה את המספרים האי זוגיים בלבד 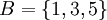 . קבוצת חסמי המלעיל של
. קבוצת חסמי המלעיל של  הינה
הינה 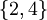 . המינימום של קבוצה זו הוא
. המינימום של קבוצה זו הוא 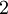 ולכן הוא החסם העליון של
ולכן הוא החסם העליון של  . אין חסם מלרע ל-
. אין חסם מלרע ל- ולכן בוודאי אין לה חסם תחתון.
ולכן בוודאי אין לה חסם תחתון.
הגדרה:
יהיו 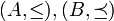 שתי קבוצות סדורות חלקית.
שתי קבוצות סדורות חלקית.
על 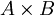 נגדיר יחס סדר חלקי הנקרא היחס המילוני
נגדיר יחס סדר חלקי הנקרא היחס המילוני  לפי
לפי
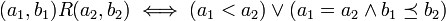
דוגמה:
עבור היחס 'קטן שווה' על 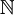 נסתכל על
נסתכל על 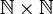 עם הסדר המילוני.
עם הסדר המילוני.
אם 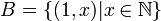 אזי
אזי 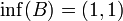 ,
, 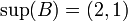 .
.
אם 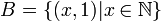 אזי
אזי 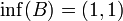 ו-
ו-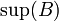 לא קיים.
לא קיים.
שימו לב ש-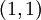 הוא איבר קטן ביותר.
הוא איבר קטן ביותר.