הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/2"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏ג)
(←‏ד)
שורה 22: שורה 22:
  
 
====ד====
 
====ד====
 +
מצא מקרה שבו אין פתרונות למערכת הלא הומוגנית, אך יש פתרון יחיד למערכת ההומוגנית
 +
 +
=====פתרון=====
 +
נביט במטריצה <math>A=\begin{pmatrix} 1 & 0 \\ 0 & 1  \\ 0 & 0 \end{pmatrix}</math> ובוקטור הפתרונות <math>A=\begin{pmatrix} 1 \\  1 \\ 1 \end{pmatrix}</math>. במערכת Ax=b ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש פתרון יחיד (0,0).
 +
 +
 +
====ה====
 +
מצא מקרה שבו אין פתרונות למערכת הלא הומוגנית, אך יש אינסוף פתרונות למערכת ההומוגנית
 +
 +
=====פתרון=====
 +
נביט במטריצה <math>A=\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}</math> ובוקטור הפתרונות <math>A=\begin{pmatrix} 0 \\  1 \end{pmatrix}</math>. במערכת Ax=b מעל הממשיים ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש אינסוף פתרונות.

גרסה מ־10:23, 19 ביולי 2011

שיעור שני

אלגברת מטריצות

ניתן לבצע את הכפל AB אם"ם מספר העמודות של A זהה למספר השורות של B. אמנם פעולת הכפל נראית משונה, אך נראה בהמשך כי היא משמעותית למדי.

תרגיל 3.4 ג-ז

נתונה מערכת של m משוואות בn נעלמים: Ax=b (זה זמן טוב לראות דוגמא ראשונה של המשמעות של כפל מטריצות). נסמן ב 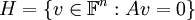H=\{v\in\mathbb{F}^n:Av=0\} את קבוצת הפתרונות של המערכת ההומוגנית המתאימה, וב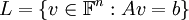L=\{v\in\mathbb{F}^n:Av=b\} את קבוצת הפתרונות של המערכת הלא-הומוגנית. הוכח את הטענות הבאות:

ג

אם L אינה קבוצה ריקה, אזי כמות הפתרונות בH שווה לכמות הפתרונות בL

פתרון

נוכיח את הטענה על ידי יצירת פונקציה חח"ע ועל בין H לבין L. יהיה 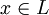x\in L כלשהו (הקיים לפי הנתון). נביט בהעתקה 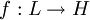f:L\rightarrow H המוגדרת ע"י 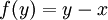f(y)=y-x. יש להוכיח כי זו אכן פונקציה מוגדרת היטב (כלומר, y-x הוא פתרון של המערכת ההומוגנית) ואז יש להראות כי זה פונקציה חח"ע ועל.

דבר ראשון, נבדוק האם y-x הינו פתרון של המערכת ההומוגנית. 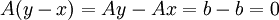A(y-x)=Ay-Ax=b-b=0 כפי שרצינו.

דבר שני, נניח כי 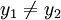y_1\neq y_2 לכן ברור ש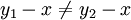y_1-x\neq y_2-x (במילים, לכל שני פתרונות שונים מL מתאימים שני פתרונות שונים בH).

דבר שלישי, נראה כי לכל פתרון y בH, יש פתרון בL הנשלח אליו. פתרון זה הינו כמובן y+x שכן 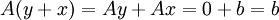A(y+x)=Ay+Ax=0+b=b.


לכן סה"כ הראנו כי לכל פתרון בL מתאים פתרון יחיד בH ולכן הקבוצות הנ"ל הן באותו גודל.

ד

מצא מקרה שבו אין פתרונות למערכת הלא הומוגנית, אך יש פתרון יחיד למערכת ההומוגנית

פתרון

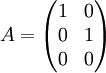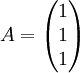נביט במטריצה A=\begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} ובוקטור הפתרונות A=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}. במערכת Ax=b ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש פתרון יחיד (0,0).


ה

מצא מקרה שבו אין פתרונות למערכת הלא הומוגנית, אך יש אינסוף פתרונות למערכת ההומוגנית

פתרון

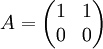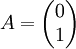נביט במטריצה A=\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} ובוקטור הפתרונות A=\begin{pmatrix} 0 \\ 1 \end{pmatrix}. במערכת Ax=b מעל הממשיים ישנה שורת סתירה, ולכן אין לה פתרונות, ואילו למערכת ההומוגנית יש אינסוף פתרונות.

מקור: https://math-wiki.com/index.php?title=88-112_לינארית_1_תיכוניסטים_קיץ_תשעא/מערך_תרגול/2&oldid=11304