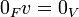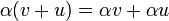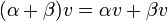הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/4"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏מרחבים וקטורים)
(←‏מרחבים וקטורים)
שורה 1: שורה 1:
 
=מרחבים וקטורים=
 
=מרחבים וקטורים=
  
−
דוגמא שכדאי שתהיה ברקע ּ<math>V=\mathbb{R}^{3}:=\{(x,y,z)\,|\, x,y,z,\in\mathbb{R}\}</math> עם '''חיבור'''
+
דוגמא שכדאי שתהיה ברקע ּ<math>V=\mathbb{R}^{3}:=\{(x,y,z)\,|\, x,y,z,\in\mathbb{R}\}</math>
−
<math>(x_{1},y_{1},z_{1})+(x_{2},y_{2},z_{2})=(x_{1}+x_{2},y_{1}+y_{2},z_{1}+z_{2})</math> ו'''כפל בסקלאר''' <math>\alpha\in\mathbb{R} , \alpha(x,y,z)=(\alpha z,\alpha y,\alpha z)</math>  הוא מרחב וקטורי.
+
 
 +
עם '''חיבור'''
 +
<math>(x_{1},y_{1},z_{1})+(x_{2},y_{2},z_{2})=(x_{1}+x_{2},y_{1}+y_{2},z_{1}+z_{2})</math>  
 +
 
 +
ו'''כפל בסקלאר''' <math>\alpha\in\mathbb{R} , \alpha(x,y,z)=(\alpha z,\alpha y,\alpha z)</math>  הוא מרחב וקטורי.
  
 
ההגדרה הפורמאלית מכלילה את הדוגמא.  
 
ההגדרה הפורמאלית מכלילה את הדוגמא.  
שורה 15: שורה 19:
  
 
#'''אקסיומות של החיבור ב <math>V</math>:'''
 
#'''אקסיומות של החיבור ב <math>V</math>:'''
−
 
 
לכל <math>v,w,u\in V</math>  מתקיים
 
לכל <math>v,w,u\in V</math>  מתקיים
−
 
 
## מוגדרות: <math>v+w\in V</math> .
 
## מוגדרות: <math>v+w\in V</math> .
 
##קיבוץ: <math>v+(u+w)=(v+u)+w</math> .
 
##קיבוץ: <math>v+(u+w)=(v+u)+w</math> .
שורה 23: שורה 25:
 
##איבר נטרלי: <math>\exists0\in V:\,\forall v\in V:0+v=v</math> .
 
##איבר נטרלי: <math>\exists0\in V:\,\forall v\in V:0+v=v</math> .
 
##איבר נגדי: <math>\forall v\in V\,\exists(-v)\in V:\, v+(-v)=0</math> .
 
##איבר נגדי: <math>\forall v\in V\,\exists(-v)\in V:\, v+(-v)=0</math> .
−
 
 
#'''אקסיומות של כפל וחיבור של שדה''' -בהגדרת שדה
 
#'''אקסיומות של כפל וחיבור של שדה''' -בהגדרת שדה
−
 
 
#'''אקסיומות כפל בסקלאר'''  
 
#'''אקסיומות כפל בסקלאר'''  
−
 
 
לכל <math>v,u\in V,\alpha,\beta\in\mathbb{F}</math> מתקיים
 
לכל <math>v,u\in V,\alpha,\beta\in\mathbb{F}</math> מתקיים
−
 
 
##מוגדרות <math>\alpha v\in V</math>  
 
##מוגדרות <math>\alpha v\in V</math>  
 
##קיבוץ: <math>\alpha(\beta v)=(\alpha\beta)v</math>  
 
##קיבוץ: <math>\alpha(\beta v)=(\alpha\beta)v</math>  

גרסה מ־12:08, 9 ביולי 2015

מרחבים וקטורים

דוגמא שכדאי שתהיה ברקע ּ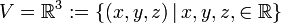V=\mathbb{R}^{3}:=\{(x,y,z)\,|\, x,y,z,\in\mathbb{R}\}

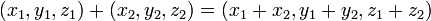
עם חיבור (x_{1},y_{1},z_{1})+(x_{2},y_{2},z_{2})=(x_{1}+x_{2},y_{1}+y_{2},z_{1}+z_{2})

וכפל בסקלאר 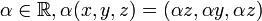\alpha\in\mathbb{R} , \alpha(x,y,z)=(\alpha z,\alpha y,\alpha z) הוא מרחב וקטורי.

ההגדרה הפורמאלית מכלילה את הדוגמא.

הגדרה: מרחב וקטורי הוא רביעיה 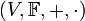(V,\mathbb{F},+,\cdot), כאשר

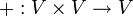
  • V היא קבוצה המוגדרת בה פעולה בינארית של חיבור (+). כלומר +:V\times V \to V
  • \mathbb{F} הוא שדה. זכרו שבשדה גם מוגדרות פעולות חיבור וכפל, לא להתבלבל עם החיבור של V וכפל בסקלאר.
  • כפל בסקלאר (\cdot) היא פעולה המקשרת בין איברי V לאיברי \mathbb{F}.

פורמאלית 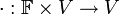\cdot : \mathbb{F}\times V \to V.

אקסיומות מרחב וקטורי:

  1. אקסיומות של החיבור ב V:

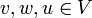לכל v,w,u\in V מתקיים

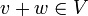    1. מוגדרות: v+w\in V .
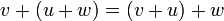    2. קיבוץ: v+(u+w)=(v+u)+w .
    3. חילוף: v+u=u+v .
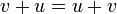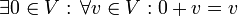    4. איבר נטרלי: \exists0\in V:\,\forall v\in V:0+v=v .
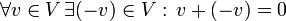    5. איבר נגדי: \forall v\in V\,\exists(-v)\in V:\, v+(-v)=0 .
  2. אקסיומות של כפל וחיבור של שדה -בהגדרת שדה
  3. אקסיומות כפל בסקלאר

לכל 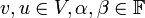v,u\in V,\alpha,\beta\in\mathbb{F} מתקיים

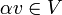
    1. מוגדרות \alpha v\in V
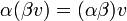
    2. קיבוץ: \alpha(\beta v)=(\alpha\beta)v
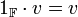
    3. כפל ביחידה (של השדה): 1_{\mathbb{F}}\cdot v=v
    4. פילוג:
      1. \alpha(v+u)=\alpha v+\alpha u
      2. (\alpha+\beta)v=\alpha v+\beta v

טרמינולוגיה: אומרים ש V מרחב וקטורי מעל \mathbb{F}.

איברי V נקראים וקטורים. איברי \mathbb{F} נקראים סקלארים.


תכונות בסיסיות:

.1 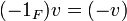(-1_{F})v=(-v)

.2 0_{F}v=0_{V}

מקור: https://math-wiki.com/index.php?title=88-112_לינארית_1_תיכוניסטים_קיץ_תשעא/מערך_תרגול/4&oldid=61795