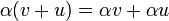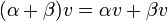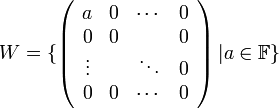הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/4"
(←דוגמאות) |
(←תתי מרחבים) |
||
| שורה 89: | שורה 89: | ||
#שלכל <math>w,u\in W,\,\alpha\in\mathbb{F}</math> מתקיים <math>\alpha u+w\in W</math>. | #שלכל <math>w,u\in W,\,\alpha\in\mathbb{F}</math> מתקיים <math>\alpha u+w\in W</math>. | ||
| − | אבחנה: <math>\{0\},V\subseteq V</math> תמיד תתי מרחבים ונקראים | + | אבחנה: <math>\{0\},V\subseteq V</math> תמיד תתי מרחבים ונקראים תתי המרחבים הטריוואלים. |
| + | |||
| + | ===דוגמאות ודוגמאות נגדיות === | ||
| + | |||
| + | 1. המישור האוקלידי <math>V=\mathbb{R}^{2}</math> מעל <math>\mathbb{F}=\mathbb{R}</math> | ||
| + | |||
| + | א. <math> W=\{(x,y)\,|\, x,y\geq 0\}</math> (הרביע החיובי) אינו תת מרחב כי | ||
| + | <math>-1(1,1)=(-1,-1)\not\notin W</math> | ||
| + | |||
| + | ב. <math>W=\{(x,y)\,|\, x,y\geq0\:\textnormal{or }x,y\leq0\}</math> (הרביע החיובי והשלילי) אינו תת מרחב כי <math>\underset{\in W}{(2,4)}+\underset{\in W}{(-3,-3)}=(-1,1)\notin W</math> | ||
| + | |||
| + | ג. <math>W=\{(x,y)|\, y=3x\}</math> קו ישר העובר בראשית הוא כן תת מרחב. נוכיח את זה בסעיף הבא: | ||
| + | |||
| + | 2. תהא <math>A\in \mathbb{F}^{m\times n}</math> מטריצה ונסתכל על אוסף הפתרונות למערכת ההומוגנית <math>Ax=0</math>. | ||
| + | פורמאלית <math>W=\{v\in \mathbb{F}^n \, :\, Av=0\} \subseteq \mathbb{F}^n </math>. | ||
| + | |||
| + | טענה <math>W\leq \mathbb{F}^n</math> תת מרחב | ||
| + | |||
| + | הוכחה: נשתמש בקריטריון המקוצר | ||
| + | # ברור ש <math>W</math> לא ריקה כי <math>0\in W</math> | ||
| + | # לכל <math>v_1,v_2\in W,\,\alpha\in\mathbb{F}</math> רוצים להראות כי <math>\alpha v_1 +v_2 \in W</math>. לפי הגדרה צריך להראות כי <math>A(\alpha v_1 +v_2)=0</math>. ואכן, <math>A(\alpha v_1 +v_2)=\alpha Av_1+Av_2=\alpha 0+0 =0+0=0</math>. | ||
| + | |||
| + | 3. מרחב המטריצות <math>V=\mathbb{F}^{n\times n}</math> מעל <math>\mathbb{F}</math> | ||
| + | א. המטריצות מסוג | ||
| + | <math>W=\{\left(\begin{array}{cccc} | ||
| + | a & 0 & \cdots & 0\\ | ||
| + | 0 & 0 & & 0\\ | ||
| + | \vdots & & \ddots & 0\\ | ||
| + | 0 & 0 & \cdots & 0 | ||
| + | \end{array}\right)|a\in\mathbb{F}\}</math> | ||
| + | הן תת מרחב. | ||
| + | |||
| + | נוכיח : | ||
| + | # ברור כי <math>W</math> אינה ריקה כי מטריצת האפס שייך ל <math>W</math> | ||
| + | (b) המטריצות הסימטריות W=\{A\in V\,|\, A^{t}=A\} ֱ הן תת מרחב )בתרגיל(. | ||
| + | |||
| + | (c) המטריצות הסימטריות איחוד עם המטריצות האנטי סימטריות W=\{A\in V\,|\, A^{t}=A\textnormal{\,\ or\,}A^{t}=-A\} אינו תת מרחב כי \left(\begin{array}{cc} | ||
| + | 0 & 1\\ | ||
| + | -1 & 0 | ||
| + | \end{array}\right),\left(\begin{array}{cc} | ||
| + | 1 & 1\\ | ||
| + | 1 & 1 | ||
| + | \end{array}\right)\in W אבל \left(\begin{array}{cc} | ||
| + | 0 & 1\\ | ||
| + | -1 & 0 | ||
| + | \end{array}\right)+\left(\begin{array}{cc} | ||
| + | 1 & 1\\ | ||
| + | 1 & 1 | ||
| + | \end{array}\right)=\left(\begin{array}{cc} | ||
| + | 1 & 1\\ | ||
| + | 0 & 1 | ||
| + | \end{array}\right)\notin W . | ||
| + | |||
| + | .3 V=\mathbb{R}_{2}[x] מרחב הפלינומים מדרגה 2 מעל \mathbb{R} . | ||
| + | |||
| + | (a) W=\mathbb{R}_{1}[x]=\{a+bx|\, a,b\in\mathbb{R}\} הינו תת מרחב כי באופן כללי \mathbb{R}_{n}[x] הוא מרחב וקטורי. | ||
| + | |||
| + | (b) W=\{a+bx|\,0\not=b\in\mathbb{R}\} הפולינומים מדרגה 1 בדיוק אינו תת מרחב. כי פולינום האפס שהוא האיבר הנטרלי ב V לא נמצא ב W 0\notin W . | ||
| + | |||
| + | .4 V=\mathbb{R} הוא מרחב וקטורי מעל \mathbb{F}=\mathbb{Q} . | ||
| + | |||
| + | (a) W=\mathbb{Q} הוא תת מרחב כי לכל v,w\in W,\,\alpha\in\mathbb{F} מתקיים \alpha v+w\in W . | ||
| + | |||
| + | .5 V=\mathbb{R} הוא מרחב וקטורי מעל \mathbb{F}=\mathbb{R} . | ||
| + | |||
| + | (a) W=\mathbb{Q} הוא אינו תת מרחב כי 1\in W,\,\sqrt{2}\in\mathbb{F} אבל 1\cdot\sqrt{2}=\sqrt{2}\notin W | ||
גרסה מ־12:39, 9 ביולי 2015
מרחבים וקטורים
דוגמא שכדאי שתהיה ברקע ּ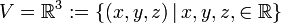
עם חיבור
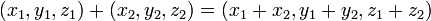
וכפל בסקלאר 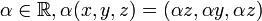 הוא מרחב וקטורי.
הוא מרחב וקטורי.
ההגדרה הפורמאלית מכלילה את הדוגמא.
הגדרה: מרחב וקטורי הוא רביעיה 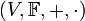 , כאשר
, כאשר
-
 היא קבוצה המוגדרת בה פעולה בינארית של חיבור (+). כלומר
היא קבוצה המוגדרת בה פעולה בינארית של חיבור (+). כלומר 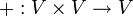
-
 הוא שדה. זכרו שבשדה גם מוגדרות פעולות חיבור וכפל, לא להתבלבל עם החיבור של
הוא שדה. זכרו שבשדה גם מוגדרות פעולות חיבור וכפל, לא להתבלבל עם החיבור של  וכפל בסקלאר.
וכפל בסקלאר. - כפל בסקלאר (
 ) היא פעולה המקשרת בין איברי V לאיברי
) היא פעולה המקשרת בין איברי V לאיברי  . פורמאלית
. פורמאלית 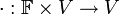
אקסיומות מרחב וקטורי:
- אקסיומות של החיבור ב
 : לכל
: לכל 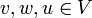 מתקיים
מתקיים
- מוגדרות:
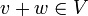 .
. - קיבוץ:
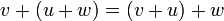 .
. - חילוף:
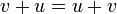 .
. - איבר נטרלי:
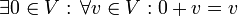 .
. - איבר נגדי:
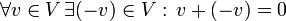 .
.
- מוגדרות:
- אקסיומות של כפל וחיבור של שדה: בהגדרת שדה
- אקסיומות כפל בסקלאר: לכל
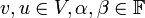 מתקיים
מתקיים
- מוגדרות
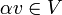
- קיבוץ:
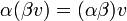
- כפל ביחידה (של השדה):
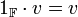
- פילוג:
- מוגדרות
טרמינולוגיה: אומרים ש  מרחב וקטורי מעל
מרחב וקטורי מעל  .
.
איברי  נקראים וקטורים. איברי
נקראים וקטורים. איברי  נקראים סקלארים.
נקראים סקלארים.
תכונות בסיסיות:
.1 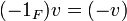
.2 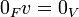
דוגמאות
1.
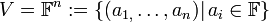 מעל
מעל 
עם חיבור 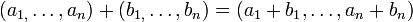
וכפל בסקלאר 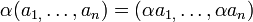
2.
מרחב המטריצות 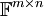 מעל שדה
מעל שדה  עם חיבור וכפל בסקלאר של מטריצות שהגדרנו כבר.
עם חיבור וכפל בסקלאר של מטריצות שהגדרנו כבר.
3.
מרחב הפולינומים מעל שדה מדרגה קטנה שווה ל n. פורמאלית
![\mathbb{F}_{n}[x]=\{a_{0}+a_{1}x+\cdots a_{n}x^{n}|\,\forall i \, a_{i}\in\mathbb{F}\}](/images/math/9/9/d/99d46bd4591e34d6066062d3ec15a0e3.png) מעל שדה
מעל שדה 
עם פעולת חיבור פולינומים וכפל בסקלאר טבעיים.
4.
מרחב הפולינומים ![\mathbb{F}[x]=\{a_{0}+a_{1}x+\cdots a_{n}x^{n}|\, a_{i}\in\mathbb{F},n\in\mathbb{N}\}](/images/math/c/7/9/c795af995ba45b9e59659f0928898123.png) עם חיבור וכפל בסקלאר מוכרים.
עם חיבור וכפל בסקלאר מוכרים.
5.
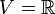 הוא מרחב וקטורי מעל
הוא מרחב וקטורי מעל 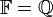 עם חיבור וכפל "רגילים".
עם חיבור וכפל "רגילים".
6. 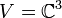 הוא מרחב וקטורי מעל
הוא מרחב וקטורי מעל 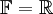 .
.
הערה: 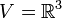 הוא אינו מרחב וקטורי מעל
הוא אינו מרחב וקטורי מעל 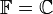 (עם חיבור וכפל בסקלאר סטנדרטים) כי
(עם חיבור וכפל בסקלאר סטנדרטים) כי 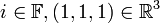 והכפל בניהם צריך להיות שייך ל
והכפל בניהם צריך להיות שייך ל  אבל
אבל 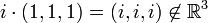
תתי מרחבים
הגדרה יהיה  מרחב וקטורי מעל
מרחב וקטורי מעל  . תת קבוצה
. תת קבוצה 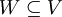 יקרא תת מרחב אם הוא מרחב וקטורי בפני עצמו ביחס לפעולות V. סימון
יקרא תת מרחב אם הוא מרחב וקטורי בפני עצמו ביחס לפעולות V. סימון 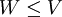
הערה: כדי לבדוק אם W\subseteq V הוא תת מרחב מספיק לבדוק
- לכל
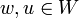 מתקיים
מתקיים - מוגדרות:
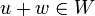 .
. - איבר נטרלי: 0 של
 נמצא ב-
נמצא ב-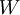
- אקסיומות כפל בסקלאר: לכל
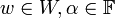 מתקיים
מתקיים
- מוגדרות
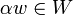
- מוגדרות
את שאר האקסיומות 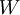 יורש מ
יורש מ  כתת קבוצה.
כתת קבוצה.
הערה: ניתן לרכז את הבדיקות הנ"ל מספיק לבדוק
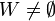
- שלכל
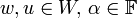 מתקיים
מתקיים 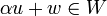 .
.
אבחנה: 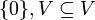 תמיד תתי מרחבים ונקראים תתי המרחבים הטריוואלים.
תמיד תתי מרחבים ונקראים תתי המרחבים הטריוואלים.
דוגמאות ודוגמאות נגדיות
1. המישור האוקלידי 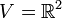 מעל
מעל 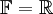
א. 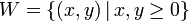 (הרביע החיובי) אינו תת מרחב כי
(הרביע החיובי) אינו תת מרחב כי
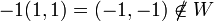
ב. עיבוד הנוסחה נכשל (שגיאת לקסינג): W=\{(x,y)\,|\, x,y\geq0\:\textnormal{or }x,y\leq0\}
(הרביע החיובי והשלילי) אינו תת מרחב כי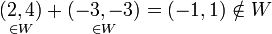
ג. 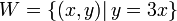 קו ישר העובר בראשית הוא כן תת מרחב. נוכיח את זה בסעיף הבא:
קו ישר העובר בראשית הוא כן תת מרחב. נוכיח את זה בסעיף הבא:
2. תהא 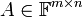 מטריצה ונסתכל על אוסף הפתרונות למערכת ההומוגנית
מטריצה ונסתכל על אוסף הפתרונות למערכת ההומוגנית 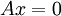 .
פורמאלית
.
פורמאלית 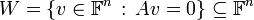 .
.
טענה 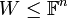 תת מרחב
תת מרחב
הוכחה: נשתמש בקריטריון המקוצר
- ברור ש
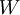 לא ריקה כי
לא ריקה כי 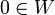
- לכל
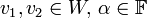 רוצים להראות כי
רוצים להראות כי 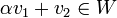 . לפי הגדרה צריך להראות כי
. לפי הגדרה צריך להראות כי 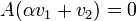 . ואכן,
. ואכן, 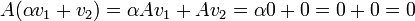 .
.
3. מרחב המטריצות 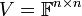 מעל
מעל  א. המטריצות מסוג
א. המטריצות מסוג
הן תת מרחב.
נוכיח :
- ברור כי
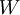 אינה ריקה כי מטריצת האפס שייך ל
אינה ריקה כי מטריצת האפס שייך ל 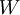
(b) המטריצות הסימטריות W=\{A\in V\,|\, A^{t}=A\} ֱ הן תת מרחב )בתרגיל(.
(c) המטריצות הסימטריות איחוד עם המטריצות האנטי סימטריות W=\{A\in V\,|\, A^{t}=A\textnormal{\,\ or\,}A^{t}=-A\} אינו תת מרחב כי \left(\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right),\left(\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right)\in W אבל \left(\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right)+\left(\begin{array}{cc} 1 & 1\\ 1 & 1 \end{array}\right)=\left(\begin{array}{cc} 1 & 1\\ 0 & 1 \end{array}\right)\notin W .
.3 V=\mathbb{R}_{2}[x] מרחב הפלינומים מדרגה 2 מעל \mathbb{R} .
(a) W=\mathbb{R}_{1}[x]=\{a+bx|\, a,b\in\mathbb{R}\} הינו תת מרחב כי באופן כללי \mathbb{R}_{n}[x] הוא מרחב וקטורי.
(b) W=\{a+bx|\,0\not=b\in\mathbb{R}\} הפולינומים מדרגה 1 בדיוק אינו תת מרחב. כי פולינום האפס שהוא האיבר הנטרלי ב V לא נמצא ב W 0\notin W .
.4 V=\mathbb{R} הוא מרחב וקטורי מעל \mathbb{F}=\mathbb{Q} .
(a) W=\mathbb{Q} הוא תת מרחב כי לכל v,w\in W,\,\alpha\in\mathbb{F} מתקיים \alpha v+w\in W .
.5 V=\mathbb{R} הוא מרחב וקטורי מעל \mathbb{F}=\mathbb{R} .
(a) W=\mathbb{Q} הוא אינו תת מרחב כי 1\in W,\,\sqrt{2}\in\mathbb{F} אבל 1\cdot\sqrt{2}=\sqrt{2}\notin W