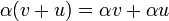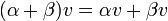הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/4"
(←דוגמא 2) |
(←סכום תתי מרחבים וסכום ישר) |
||
| שורה 365: | שורה 365: | ||
הגדרה: הסכום <math>W_1+W_2</math> יקרא '''סכום ישר''' אם <math>W_1\cap W_2 = \{0\}</math> | הגדרה: הסכום <math>W_1+W_2</math> יקרא '''סכום ישר''' אם <math>W_1\cap W_2 = \{0\}</math> | ||
| + | |||
| + | דוגמאות: | ||
| + | 1. ב <math>V=\mathbb{R}^3</math> נגדיר שני תת מרחב | ||
| + | <math>W_1=\{\alpha\begin{pmatrix}1\\ 1\\ 0 \end{pmatrix} | ||
| + | :\, \alpha \in \mathbb{R} \} </math> | ||
| + | |||
| + | <math>W_2=\{\alpha\begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix} | ||
| + | :\, \alpha \in \mathbb{R} \} </math> | ||
| + | |||
| + | אזי | ||
| + | |||
| + | <math>W_1+W_2=\{w_1+w_2:\, w_1\in W_1, w_2\in W_2\} = | ||
| + | \{\alpha_1\begin{pmatrix}1\\ 1\\ 0 \end{pmatrix} | ||
| + | + \alpha_2\begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix} | ||
| + | :\, \alpha_1,\alpha_2 \in \mathbb{R} \} = \\ | ||
| + | \{\begin{pmatrix}\alpha_1\\ \alpha_1+\alpha_2\\ \alpha_2 \end{pmatrix} | ||
| + | :\, \alpha_1,\alpha_2 \in \mathbb{R}\} | ||
| + | </math> | ||
| + | |||
| + | 2. באופן כללי | ||
גרסה מ־18:34, 9 ביולי 2015
תוכן עניינים
מרחבים וקטורים
דוגמא שכדאי שתהיה ברקע ּ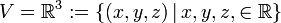
עם חיבור
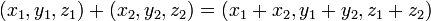
וכפל בסקלאר 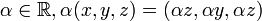 הוא מרחב וקטורי.
הוא מרחב וקטורי.
ההגדרה הפורמאלית מכלילה את הדוגמא.
הגדרה: מרחב וקטורי הוא רביעיה 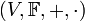 , כאשר
, כאשר
-
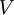 היא קבוצה המוגדרת בה פעולה בינארית של חיבור (+). כלומר
היא קבוצה המוגדרת בה פעולה בינארית של חיבור (+). כלומר 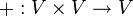
-
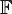 הוא שדה. זכרו שבשדה גם מוגדרות פעולות חיבור וכפל, לא להתבלבל עם החיבור של
הוא שדה. זכרו שבשדה גם מוגדרות פעולות חיבור וכפל, לא להתבלבל עם החיבור של 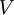 וכפל בסקלאר.
וכפל בסקלאר. - כפל בסקלאר (
 ) היא פעולה המקשרת בין איברי V לאיברי
) היא פעולה המקשרת בין איברי V לאיברי 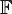 . פורמאלית
. פורמאלית 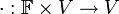
אקסיומות מרחב וקטורי:
- אקסיומות של החיבור ב
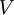 : לכל
: לכל 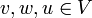 מתקיים
מתקיים
- מוגדרות:
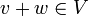 .
. - קיבוץ:
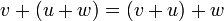 .
. - חילוף:
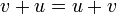 .
. - איבר נטרלי:
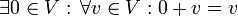 .
. - איבר נגדי:
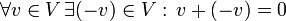 .
.
- מוגדרות:
- אקסיומות של כפל וחיבור של שדה: בהגדרת שדה
- אקסיומות כפל בסקלאר: לכל
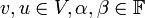 מתקיים
מתקיים
- מוגדרות
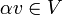
- קיבוץ:
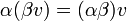
- כפל ביחידה (של השדה):
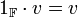
- פילוג:
- מוגדרות
טרמינולוגיה: אומרים ש 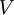 מרחב וקטורי מעל
מרחב וקטורי מעל 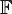 .
.
איברי 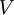 נקראים וקטורים. איברי
נקראים וקטורים. איברי 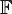 נקראים סקלארים.
נקראים סקלארים.
תכונות בסיסיות:
.1 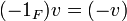
.2 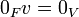
דוגמאות
1.
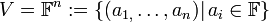 מעל
מעל 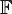
עם חיבור 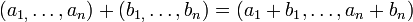
וכפל בסקלאר 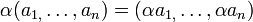
2.
מרחב המטריצות 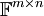 מעל שדה
מעל שדה 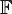 עם חיבור וכפל בסקלאר של מטריצות שהגדרנו כבר.
עם חיבור וכפל בסקלאר של מטריצות שהגדרנו כבר.
3.
מרחב הפולינומים מעל שדה מדרגה קטנה שווה ל n. פורמאלית
![\mathbb{F}_{n}[x]=\{a_{0}+a_{1}x+\cdots a_{n}x^{n}|\,\forall i \, a_{i}\in\mathbb{F}\}](/images/math/9/9/d/99d46bd4591e34d6066062d3ec15a0e3.png) מעל שדה
מעל שדה 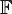
עם פעולת חיבור פולינומים וכפל בסקלאר טבעיים.
4.
מרחב הפולינומים ![\mathbb{F}[x]=\{a_{0}+a_{1}x+\cdots a_{n}x^{n}|\, a_{i}\in\mathbb{F},n\in\mathbb{N}\}](/images/math/c/7/9/c795af995ba45b9e59659f0928898123.png) עם חיבור וכפל בסקלאר מוכרים.
עם חיבור וכפל בסקלאר מוכרים.
5.
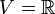 הוא מרחב וקטורי מעל
הוא מרחב וקטורי מעל 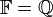 עם חיבור וכפל "רגילים".
עם חיבור וכפל "רגילים".
6. 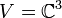 הוא מרחב וקטורי מעל
הוא מרחב וקטורי מעל 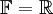 .
.
הערה: 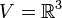 הוא אינו מרחב וקטורי מעל
הוא אינו מרחב וקטורי מעל 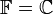 (עם חיבור וכפל בסקלאר סטנדרטים) כי
(עם חיבור וכפל בסקלאר סטנדרטים) כי 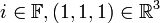 והכפל בניהם צריך להיות שייך ל
והכפל בניהם צריך להיות שייך ל 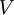 אבל
אבל 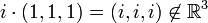
תתי מרחבים
הגדרה יהיה 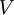 מרחב וקטורי מעל
מרחב וקטורי מעל 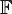 . תת קבוצה
. תת קבוצה 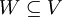 יקרא תת מרחב אם הוא מרחב וקטורי בפני עצמו ביחס לפעולות V. סימון
יקרא תת מרחב אם הוא מרחב וקטורי בפני עצמו ביחס לפעולות V. סימון 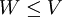
הערה: כדי לבדוק אם 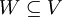 הוא תת מרחב מספיק לבדוק
הוא תת מרחב מספיק לבדוק
- לכל
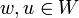 מתקיים
מתקיים - מוגדרות:
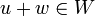 .
. - איבר נטרלי: 0 של
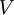 נמצא ב-
נמצא ב-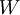
- אקסיומות כפל בסקלאר: לכל
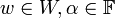 מתקיים
מתקיים
- מוגדרות
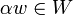
- מוגדרות
את שאר האקסיומות 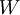 יורש מ
יורש מ 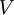 כתת קבוצה.
כתת קבוצה.
הערה: ניתן לרכז את הבדיקות הנ"ל מספיק לבדוק
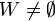
- שלכל
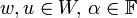 מתקיים
מתקיים 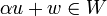 .
.
אבחנה: 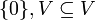 תמיד תתי מרחבים ונקראים תתי המרחבים הטריוואלים.
תמיד תתי מרחבים ונקראים תתי המרחבים הטריוואלים.
דוגמאות ודוגמאות נגדיות
1. המישור האוקלידי  מעל
מעל 
א. 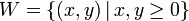 (הרביע החיובי) אינו תת מרחב כי
(הרביע החיובי) אינו תת מרחב כי
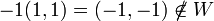
ב. עיבוד הנוסחה נכשל (שגיאת לקסינג): W=\{(x,y)\,|\, x,y\geq0\:\text{ or }x,y\leq0\}
(הרביע החיובי והשלילי) אינו תת מרחב כי 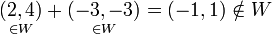
ג. 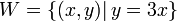 קו ישר העובר בראשית הוא כן תת מרחב. נוכיח את זה בסעיף הבא:
קו ישר העובר בראשית הוא כן תת מרחב. נוכיח את זה בסעיף הבא:
2. תהא 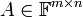 מטריצה ונסתכל על אוסף הפתרונות למערכת ההומוגנית
מטריצה ונסתכל על אוסף הפתרונות למערכת ההומוגנית 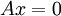 .
פורמאלית
.
פורמאלית 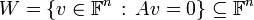 .
.
טענה 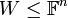 תת מרחב
תת מרחב
הוכחה: נשתמש בקריטריון המקוצר
- ברור ש
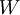 לא ריקה כי
לא ריקה כי 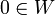
- לכל
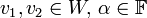 רוצים להראות כי
רוצים להראות כי 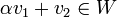 . לפי הגדרה צריך להראות כי
. לפי הגדרה צריך להראות כי 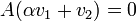 . ואכן,
. ואכן, 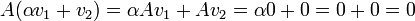 .
.
3. מרחב המטריצות 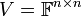 מעל
מעל 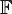 א. המטריצות מסוג
א. המטריצות מסוג
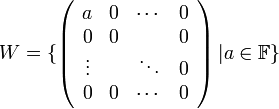 הן תת מרחב.
הן תת מרחב.
נוכיח :
- ברור כי
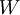 אינה ריקה כי מטריצת האפס שייך ל
אינה ריקה כי מטריצת האפס שייך ל 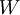
- לכל
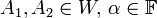 רוצים להראות ש
רוצים להראות ש 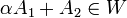 כלומר להראות שהמטריצה
כלומר להראות שהמטריצה 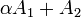 כולה אפסים פרט (אולי) למקום
כולה אפסים פרט (אולי) למקום 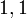 וזה אכן כך בגלל שזאת הצורה של
וזה אכן כך בגלל שזאת הצורה של 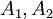
ב. המטריצות הסימטריות 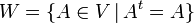 והמטריצות האנטי-סימטריות
והמטריצות האנטי-סימטריות 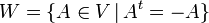 שתיהן תתי מרחב.
שתיהן תתי מרחב.
הוכחה (עבור הסימטריות)
- ברור כי
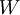 אינה ריקה כי מטריצת האפס שייך ל
אינה ריקה כי מטריצת האפס שייך ל 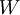
- לכל
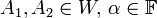 רוצים להראות ש
רוצים להראות ש 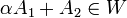 כלומר להראות שהמטריצה
כלומר להראות שהמטריצה 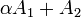 סימטרית. נתון כי
סימטרית. נתון כי 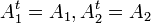 . כעת מחוקי שיחלוף
. כעת מחוקי שיחלוף
נקבל כי 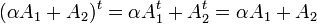 .
.
ג.המטריצות הסימטריות איחוד עם המטריצות האנטי סימטריות
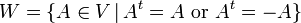 אינו תת מרחב כי
המטריצות
אינו תת מרחב כי
המטריצות
 שייכות ל
שייכות ל  אבל החיבור שלהם לא.
אבל החיבור שלהם לא.
ד. המטריצות משולשיות/אלכסוניות/סקלאריות הן תת מרחב.
ה. המטריצות 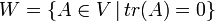 הן תת מרחב
הן תת מרחב
הוכחה
- ברור כי
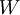 אינה ריקה כי מטריצת האפס שייך ל
אינה ריקה כי מטריצת האפס שייך ל 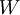
- לכל
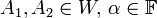 רוצים להראות ש
רוצים להראות ש 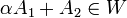 כלומר להראות שעקבה של המטריצה
כלומר להראות שעקבה של המטריצה 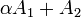 שווה 0. נתון כי
שווה 0. נתון כי 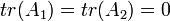 . כעת מחוקי עקבה
. כעת מחוקי עקבה
נקבל כי 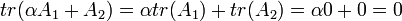 .
.
4. ![V=\mathbb{R}_{2}[x]](/images/math/f/7/3/f73cc35842c78e71bd2b26bb136b5c6a.png) מרחב הפלינומים מדרגה 2 מעל
מרחב הפלינומים מדרגה 2 מעל 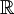 .
.
א. ![W=\mathbb{R}_{1}[x]=\{a+bx|\, a,b\in\mathbb{R}\}](/images/math/9/f/4/9f4af47c0544b890cd2e588c3fafd123.png) הינו תת מרחב כי באופן כללי
הינו תת מרחב כי באופן כללי ![\mathbb{R}_{n}[x]](/images/math/3/a/1/3a119efd785cc2d1f85c57052e840b07.png) הוא מרחב וקטורי (והפעולות מוגדרות באופן זהה לכל המרחבים).
הוא מרחב וקטורי (והפעולות מוגדרות באופן זהה לכל המרחבים).
ב. 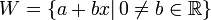 הפולינומים מדרגה 1 בדיוק אינו תת מרחב. כי פולינום האפס שהוא האיבר הנטרלי ב
הפולינומים מדרגה 1 בדיוק אינו תת מרחב. כי פולינום האפס שהוא האיבר הנטרלי ב 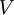 לא נמצא ב
לא נמצא ב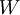 .
.
חיתוך תתי מרחבים
משפט: יהי 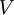 מרחב וקטורי מעל
מרחב וקטורי מעל 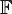 . יהיו
. יהיו 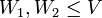 תתי מרחבים.
אזי חיתוך תתי המרחבים
תתי מרחבים.
אזי חיתוך תתי המרחבים 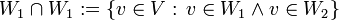 הינו תת מרחב.
הינו תת מרחב.
הערה: זהו התת מרחב הכי "גדול" שמוכל ב 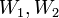 . פורמאלית, כל תת מרחב
. פורמאלית, כל תת מרחב 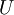 המקיים כי
המקיים כי 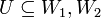 יקיים כי
יקיים כי 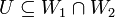
דוגמא 1
1. יהי 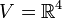 . נגדיר שתי תת מרחבים
. נגדיר שתי תת מרחבים
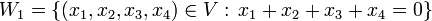
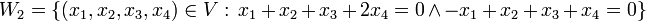
נמצא את 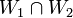
נשים לב שנוכל לאפיין את תתי המרחבים בצורה הבאה:
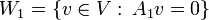
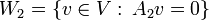
כאשר
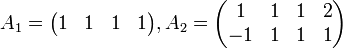
כמו שראינו אלו תת מרחבים. כעת
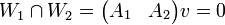
ולכן צריך בסה"כ למצוא פתרון למערכת לא הומוגנית. נעשה זאת עיבוד הנוסחה נכשל (שגיאת תחביר): \begin{pmatrix} 1 &1 &1 &1 \\ 1 &1 &1 &2 \\ -1 &1 &1 &1 \end{pmatrix} \to \\ \begin{pmatrix} 1 &1 &1 &1 \\ 0 &0 &0 &1 \\ 0 &2 &2 &2 \end{pmatrix} \to \begin{pmatrix} 1 &1 &1 &1 \\ 0 &1 &1 &1\\ 0 &0 &0 &1 \end{pmatrix} \to \begin{pmatrix} 1 &1 &1 &0 \\ 0 &1 &1 &0\\ 0 &0 &0 &1 \end{pmatrix} \to \begin{pmatrix} 1 &0 &0 &0 \\ 0 &1 &1 &0\\ 0 &0 &0 &1 \end{pmatrix}
התשובה הסופית
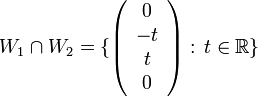
דוגמא 2
יהי 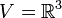 . נגדיר שתי תת מרחבים
. נגדיר שתי תת מרחבים
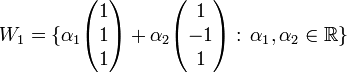
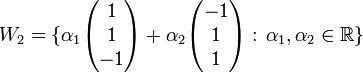
נמצא את החיתוך בניהם
צריך למצוא סקלארים  המקיימים
המקיימים
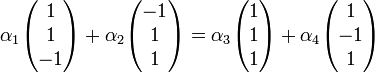
שימו לב שאם מצאנו ארבעה סקלארים שמקימים את המשוואה לעיל אז אנחנו יודעים שהוקטור הזה במשוואה. עוד שימו לב שאם יודעים שהשיוויון מתקיים מספיק לדעת את 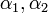 או את
או את 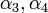 כדי לחשב את הוקטור עצמו (כי שני אגפי השיוויון שווים).
כדי לחשב את הוקטור עצמו (כי שני אגפי השיוויון שווים).
בעצם, זה שוב לפתור מערכת משוואות כאשר הנעלמים הם 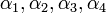 . הנה המערכת (אחרי שנעביר אגף):
. הנה המערכת (אחרי שנעביר אגף):
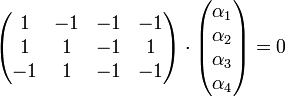
נדרג ונמשיך
עיבוד הנוסחה נכשל (שגיאת תחביר): \begin{pmatrix} 1 &-1 &-1 & -1\\ 1 &1 &-1 &1\\ -1 &1 &-1 & -1 \end{pmatrix} \to \begin{pmatrix} 1 &-1 &-1 & -1\\ 0 &2 & 0 & 2\\ 0 &0 &-2 & -2 \end{pmatrix} \to \\ \begin{pmatrix} 1 &-1 &-1 & -1\\ 0 &1 & 0 & 1\\ 0 &0 &-1 & -1 \end{pmatrix} \to \begin{pmatrix} 1 &-1 &0 &0\\ 0 &1 & 0 & 1\\ 0 &0 &-1 & -1 \end{pmatrix} \to \begin{pmatrix} 1 &0 &0 &1\\ 0 &1 & 0 & 1\\ 0 &0 &-1 & -1 \end{pmatrix}
קיבלנו כי התנאי היחידי המתקיים בין 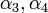 הוא
הוא 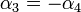 . ובמקרה שהתנאי מתקיים יש פתרון למערכת המשוואות.
. ובמקרה שהתנאי מתקיים יש פתרון למערכת המשוואות.
לכן התשובה הסופית
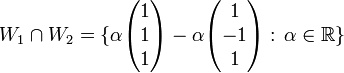
דוגמא 3
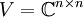 מעל
מעל 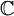 . יהיו
. יהיו 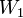 תת מרחב של המטריצות הסימטריות ו
תת מרחב של המטריצות הסימטריות ו 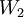 תת המרחב של המטריצות האנטי סימטריות אזי:
תת המרחב של המטריצות האנטי סימטריות אזי:
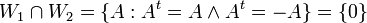
הוכחה:
ישירות- אם  גם סימטרית וגם אנטי סימטרית אזי מתקיים
גם סימטרית וגם אנטי סימטרית אזי מתקיים 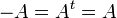 . נעביר אגף ונקבל
. נעביר אגף ונקבל 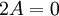 . נחלק ב 2 ונקבל כי
. נחלק ב 2 ונקבל כי 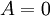
סכום תתי מרחבים
יהי 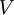 מרחב וקטורי מעל
מרחב וקטורי מעל 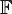 . יהיו
. יהיו 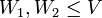 תתי מרחבים.
נרצה למצוא את התת מרחב הכי "קטן" שמכיל את
תתי מרחבים.
נרצה למצוא את התת מרחב הכי "קטן" שמכיל את 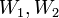 . נסמן תת מרחב זה ב
. נסמן תת מרחב זה ב 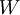 אז פורמאלית, נרצה כי כל תת מרחב
אז פורמאלית, נרצה כי כל תת מרחב 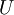 המקיים
המקיים 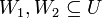 בהכרח יקיים גם
בהכרח יקיים גם 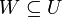 .
.
יש שיחשבו שהתת מרחב הכי קטן שמכיל את 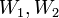 הוא האיחוד את
הוא האיחוד את 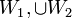 .
אבל התשובה שגויה כיוון שהאיחוד לא בהכרח תת מרחב כפי שנוכיח בתרגיל הבא.
.
אבל התשובה שגויה כיוון שהאיחוד לא בהכרח תת מרחב כפי שנוכיח בתרגיל הבא.
תרגיל:
יהי 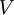 מרחב וקטורי מעל
מרחב וקטורי מעל 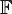 . יהיו
. יהיו 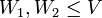 תתי מרחבים. אזי
תתי מרחבים. אזי
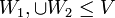 אמ"מ (
אמ"מ (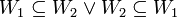 ) כלומר אחד מתת המרחב מוכל בשני.
) כלומר אחד מתת המרחב מוכל בשני.
הוכחה:
כיוון ראשון (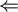 ): פשוט, אם אחד מוכל בשני אזי האיחוד שווה ל
): פשוט, אם אחד מוכל בשני אזי האיחוד שווה ל 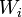 (כאשר
(כאשר 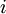 שווה ל-1 או 2, תלוי במקרה) שהוא תת מרחב.
שווה ל-1 או 2, תלוי במקרה) שהוא תת מרחב.
כיוון שני (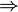 ): נניח בשלילה כי (
): נניח בשלילה כי (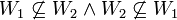 ) אזי קיימים עיבוד הנוסחה נכשל (שגיאת לקסינג): w_1\in W_1\setminus W_2 \
) אזי קיימים עיבוד הנוסחה נכשל (שגיאת לקסינג): w_1\in W_1\setminus W_2 \
וגם עיבוד הנוסחה נכשל (שגיאת לקסינג): w_2\in W_2\setminus W_1 \
. שני הוקטורים 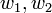 נמצאים באיחוד ולכן גם הסכום שלהם
נמצאים באיחוד ולכן גם הסכום שלהם 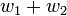 נמצא באיחוד כי נתון שהוא תת מרחב. כעת מהגדרת האיחוד
נמצא באיחוד כי נתון שהוא תת מרחב. כעת מהגדרת האיחוד 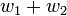 נמצא ב
נמצא ב 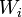 (כאשר
(כאשר 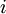 שווה ל-1 או 2, תלוי במקרה). בה"כ נניח
שווה ל-1 או 2, תלוי במקרה). בה"כ נניח 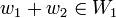 . כיוון ש
. כיוון ש 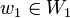 אזי חיסור שני הוקטורים
אזי חיסור שני הוקטורים 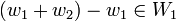 נמצא גם כן ב
נמצא גם כן ב 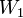 אבל החיסור שווה ל
אבל החיסור שווה ל 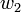 . סתירה לכך ש
. סתירה לכך ש 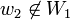
סכום תתי מרחבים וסכום ישר
הגדרה: 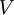 מרחב וקטורי מעל
מרחב וקטורי מעל 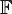 . יהיו
. יהיו 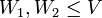 תתי מרחבים.
אזי סכום תתי המרחבים
תתי מרחבים.
אזי סכום תתי המרחבים 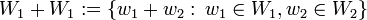 הינו תת מרחב.
הינו תת מרחב.
הערה: זהו התת מרחב הכי "קטן" המכיל את שני תת המרחב. פורמאלית, כל תת מרחב 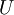 המקיים
כי
המקיים
כי 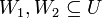 יקיים כי
יקיים כי 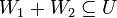
הגדרה: הסכום 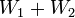 יקרא סכום ישר אם
יקרא סכום ישר אם 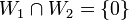
דוגמאות:
1. ב 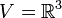 נגדיר שני תת מרחב
נגדיר שני תת מרחב
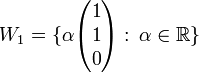
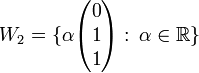
אזי
עיבוד הנוסחה נכשל (שגיאת תחביר): W_1+W_2=\{w_1+w_2:\, w_1\in W_1, w_2\in W_2\} = \{\alpha_1\begin{pmatrix}1\\ 1\\ 0 \end{pmatrix} + \alpha_2\begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix} :\, \alpha_1,\alpha_2 \in \mathbb{R} \} = \\ \{\begin{pmatrix}\alpha_1\\ \alpha_1+\alpha_2\\ \alpha_2 \end{pmatrix} :\, \alpha_1,\alpha_2 \in \mathbb{R}\}
2. באופן כללי