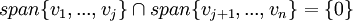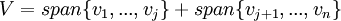הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/5"

גרסה מ־17:24, 12 ביולי 2015

תוכן עניינים

1 צירופים לינאריים והמרחב הנפרש (span)
- 1.1 תכונות
- 1.2 תרגילים
  - 1.2.1 תרגיל 1
    - 1.2.1.1 פתרון
2 תלות לינארית
3 בסיס ומימד
4 משפט המימדים

צירופים לינאריים והמרחב הנפרש (span)

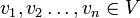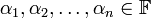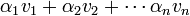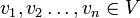הגדרה: יהיה $V$ מרחב וקטורי מעל $\mathbb{F}$ . יהיו $v_{1},v_{2}\dots,v_{n}\in V$ ו $\alpha_{1},\alpha_{2},\dots,\alpha_{n}\in\mathbb{F}$ אזי ביטוי מהצורה $\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots\alpha_{n}v_{n}$ נקרא צירוף לינארי (צ"ל) של $v_{1},v_{2}\dots,v_{n}\in V$ .

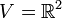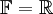לדוגמא: $V=\mathbb{R}^{2}$ מעל $\mathbb{F}=\mathbb{R}$ . אזי

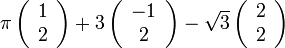
$\pi\left(\begin{array}{c} 1\\ 2 \end{array}\right)+3\left(\begin{array}{c} -1\\ 2 \end{array}\right)-\sqrt{3}\left(\begin{array}{c} 2\\ 2 \end{array}\right)$

הוא צירוף לינארי.

הגדרה: המרחב הנפרש על ידי הוקטורים 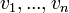$v_1,...,v_n$ מוגדר להיות קבוצת (אוסף) כל הצירופים הלינאריים של הוקטורים הללו. כלומר,

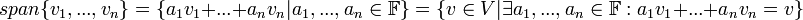$span\{v_1,...,v_n\}=\{ a_1v_1+...+a_nv_n | a_1,...,a_n\in\mathbb{F}\}=\{v\in V|\exists a_1,...,a_n\in\mathbb{F}:a_1v_1+...+a_nv_n=v\}$ .

באופן כללי: תהא 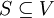$S\subseteq V$ תת קבוצה של מ"ו (ייתכן קבוצה אין סופית) אזי

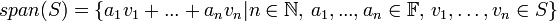
$span(S)=\{ a_1v_1+...+a_nv_n | n\in \mathbb{N}, \, a_1,...,a_n\in\mathbb{F}, \, v_1,\dots,v_n\in S\}$

באופן שקול 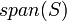$span(S)$ הוא איחוד כל הצירופים הלינאריים של כל תתי הקבוצות הסופיות של $S$ .

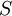הערה: 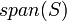$span(S)$ הינו תמיד תת-מרחב כפי שקל להוכיח באמצעות הקריטריון המקוצר - צירוף לינארי של צירופים לינאריים הינו צירוף לינארי בעצמו. בנוסף הוא התת מרחבב הקטן ביותר (מינימום לפי יחס ההכלה) המכיל את הקבוצה אותה הוא פורש

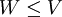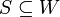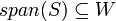
כלומר אם ת"מ $W\leq V$ מקיים $S\subseteq W$ אזי $span(S)\subseteq W$

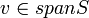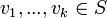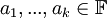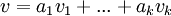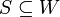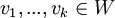הוכחה אם $v\in spanS$ אזי קיימים וקטורים וסקלרים $v_1,...,v_k\in S$ , $a_1,...,a_k\in\mathbb{F}$ כך שמתקיים $v=a_1v_1+...+a_kv_k$ . מתוך הנתון ש $S\subseteq W$ נובע ש $v_1,...,v_k\in W$ ולכן מתוך סגירות לכפל וסקלר וחיבור 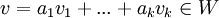$v=a_1v_1+...+a_kv_k\in W$ משל.

הערה: אם 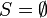$S=\emptyset$ קבוצה ריקה אזי מגדירים פורמאלית כי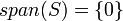 $span(S)=\{0\}$

תכונות

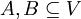יהיה $V$ מ"ו. יהיו $A,B\subseteq V$ תתי קבוצות ו 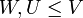$W,U\leq V$ תתי מרחבים. אזי

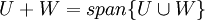$U+W=span\{U\cup W\}$ , וכפי שאמרנו הסכום הינו תת המרחב הקטן ביותר המכיל את שני תתי המרחבים.
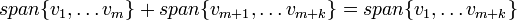
בתירגול הקודם ראינו כי $span\{v_1,\dots v_m\}+span\{v_{m+1},\dots v_{m+k}\}=span\{v_1,\dots v_{m+k}\}$
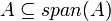
$A\subseteq span(A)$
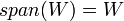$span(W)=W$ (רק אם 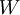$W$ ת"מ!)
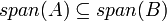
$span(A)\subseteq span(B)$
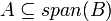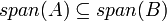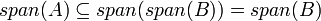מסקנה $A\subseteq span(B)$ אזי $span(A)\subseteq span(B)$ (הוכחה $span(A)\subseteq span(span(B))=span(B)$ )

תרגילים

תרגיל 1

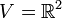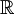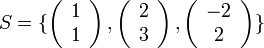
במרחב הוקטורי $V=\mathbb{R}^{2}$ מעל $\mathbb{R}$ נגדיר $S=\{\left(\begin{array}{c} 1\\ 1 \end{array}\right),\left(\begin{array}{c} 2\\ 3 \end{array}\right),\left(\begin{array}{c} -2\\ 2 \end{array}\right)\}$

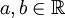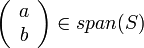
מצא עבור אילו $a,b\in\mathbb{R}$ מתקיים כי $\left(\begin{array}{c} a\\ b \end{array}\right)\in span(S)$

פתרון

תלות לינארית

דיברנו על כך שצירופים לינאריים הינם כל הסכומים (כולל כפל בסקלרים) של הוקטורים הנתונים. אם נסתכל על פרישה באופן גיאומטרי, אנו רואים שעל ידי וקטורים נפרשים: קו ישר, מישור, מרחב או משהו 4 מימדי ומעלה. כעת, אנו רוצים לראות אילו מהוקטורים "מיותר" כלומר, אם אנחנו יודעים ש10 וקטורים פורשים מישור מסויים, כמה וקטורים מהם אפשר להסיר ועדיין לקבל את אותו המישור? במקרה וניתן להסיר וקטור כלשהו, קבוצה הוקטורים תקרא תלויה לינארית.

באופן פורמאלי:

הגדרות:

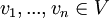יהא $V$ מ"ו מעל $\mathbb{F}$ . יהיו וקטורים $v_1,...,v_n\in V$ כלשהם אזי

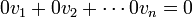הצ"ל הטריוואלי הוא צירוף לינארי שכל המקדמים שווים 0 (ואז גם הצירוף שלהם שווה 0). כלומר הצירוף לינארי $0v_{1}+0v_{2}+\cdots0v_{n}=0$ .
נאמר ש 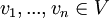$v_1,...,v_n\in V$ בילתי תלויים לינארית אם אם הצ"ל היחידי שמתאפס הוא הצ"ל הטרוויאלי. באופן שקול אם יש צ"ל שמתאפס אזי הוא הצ"ל הטרוויאלי. ובסימונים: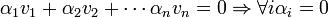 $\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots\alpha_{n}v_{n}=0 \Rightarrow \forall i \alpha_i = 0$
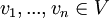$v_1,...,v_n\in V$ יקראו תלויים לינארית אם הם לא בלתי תלויים לינארית. באופן שקול אם קיימים סקלרים 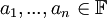$a_1,...,a_n\in\mathbb{F}$ לא כולם אפס כך שמתקיים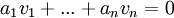 $a_1v_1+...+a_nv_n=0$

הגדרה (הכלל): קבוצה 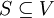$S\subseteq V$ נקראת תלוייה לינארית אם קיימת בתוכה קבוצה סופית כלשהי של וקטורים, כך שוקטוריה תלויים לינארית לפי ההגדרה לעיל. [לא נתעסק בקורס זה בקבוצת אינסופיות בת"ל, אבל אתם יותר ממוזמנים לנסות לחשוב על מרחב וקטורי בעל קבוצה אינסופית בת"ל של וקטורים.]

הערה: הקבוצה הריקה 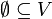$\emptyset \subseteq V$ מוגדרת כקבוצה בת"ל.

דוגמאות

דוגמא 1

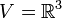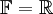
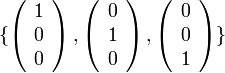$V=\mathbb{R}^{3}$ מעל $\mathbb{F}=\mathbb{R}$ $\{\left(\begin{array}{c} 1\\ 0\\ 0 \end{array}\right),\left(\begin{array}{c} 0\\ 1\\ 0 \end{array}\right),\left(\begin{array}{c} 0\\ 0\\ 1 \end{array}\right)\}$ בת"ל כי

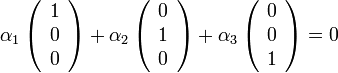
$\alpha_{1}\left(\begin{array}{c} 1\\ 0\\ 0 \end{array}\right)+\alpha_{2}\left(\begin{array}{c} 0\\ 1\\ 0 \end{array}\right)+\alpha_{3}\left(\begin{array}{c} 0\\ 0\\ 1 \end{array}\right)=0$

פירושו

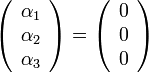
$\left(\begin{array}{c} \alpha_{1}\\ \alpha_{2}\\ \alpha_{3} \end{array}\right)=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right)$

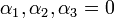שזה גורר $\alpha_{1},\alpha_{2},\alpha_{3}=0$ .

דוגמא 2

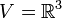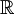2. (דוגמא מייצגת) $V=\mathbb{R}^{3}$ מעל $\mathbb{R}$ . האם הקבוצה 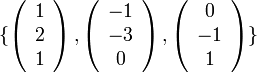$\{\left(\begin{array}{c} 1\\ 2\\ 1 \end{array}\right),\left(\begin{array}{c} -1\\ -3\\ 0 \end{array}\right),\left(\begin{array}{c} 0\\ -1\\ 1 \end{array}\right)\}$ בת"ל?

נתבונן ב 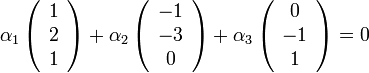$\alpha_{1}\left(\begin{array}{c} 1\\ 2\\ 1 \end{array}\right)+\alpha_{2}\left(\begin{array}{c} -1\\ -3\\ 0 \end{array}\right)+\alpha_{3}\left(\begin{array}{c} 0\\ -1\\ 1 \end{array}\right)=0$ ונמיר אותו להצגה מטריצית

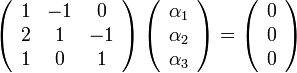
$\left(\begin{array}{ccc} 1 & -1 & 0\\ 2 & 1 & -1\\ 1 & 0 & 1 \end{array}\right)\left(\begin{array}{c} \alpha_{1}\\ \alpha_{2}\\ \alpha_{3} \end{array}\right)=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right)$

כעת השאלה שקולה האם יש פתרון לא טריאלי למערכת. נדרג ונבדוק

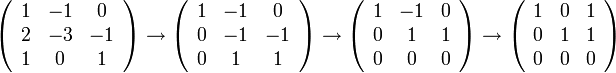
$\left(\begin{array}{ccc} 1 & -1 & 0\\ 2 & -3 & -1\\ 1 & 0 & 1 \end{array}\right)\to\left(\begin{array}{ccc} 1 & -1 & 0\\ 0 & -1 & -1\\ 0 & 1 & 1 \end{array}\right)\to\left(\begin{array}{ccc} 1 & -1 & 0\\ 0 & 1 & 1\\ 0 & 0 & 0 \end{array}\right)\to\left(\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 0 & 0 \end{array}\right)$

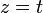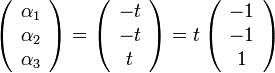לכל הצבה $z=t$ נקבל $\left(\begin{array}{c} \alpha_{1}\\ \alpha_{2}\\ \alpha_{3} \end{array}\right)= \left(\begin{array}{c} -t\\ -t\\ t \end{array}\right)=t\left(\begin{array}{c} -1\\ -1\\ 1 \end{array}\right)$ פתרון לא טרוויאלי. כלומר הוקטורים הנ"ל ת"ל.

אם רוצים לראות את זה מפורש ניקח למשל 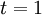$t=1$ ונקבל צ"ל לא טריוואלי שמתאפס

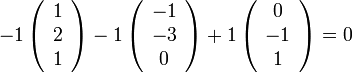
$-1\left(\begin{array}{c} 1\\ 2\\ 1 \end{array}\right)-1\left(\begin{array}{c} -1\\ -3\\ 0 \end{array}\right)+1\left(\begin{array}{c} 0\\ -1\\ 1 \end{array}\right)=0$

דוגמא 3

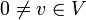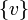יהי $0\not=v\in V$ אזי $\{v\}$ קבוצה בת"ל.

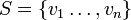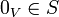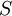לחילופין יהי $S=\{v_{1}\dots,v_{n}\}$ כך ש $0_{V}\in S$ אזי $S$ ת"ל (ניקח צ"ל שכל המקדמים שווים אפס פרט למקדם של וקטור האפס שניקח להיות שווה 1).

דוגמא 4

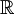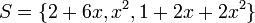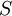$V=\mathbb{R}_{2}[x]$ מרחב הפלינומים עד דרגה 2 מעל $\mathbb{R}$ תהא $S=\{2+6x,x^{2},1+2x+2x^{2}\}$ . האם $S$ בת"ל?

פתרון: צריך לבדוק האם 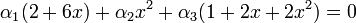$\alpha_{1}(2+6x)+\alpha_{2}x^{2}+\alpha_{3}(1+2x+2x^{2})=0$ גורר שזה הצ"ל הטריאלי.

לפי השוואת מקדמים נקבל כי : 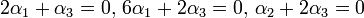$2\alpha_{1}+\alpha_{3}=0,\,6\alpha_{1}+2\alpha_{3}=0,\,\alpha_{2}+2\alpha_{3}=0$

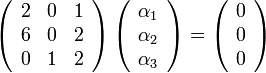
ובצורה מטריצית $\left(\begin{array}{ccc} 2 & 0 & 1\\ 6 & 0 & 2\\ 0 & 1 & 2 \end{array}\right)\left(\begin{array}{c} \alpha_{1}\\ \alpha_{2}\\ \alpha_{3} \end{array}\right)=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right)$

נבדוק אם למערכת יש פתרון לא טריאלי.

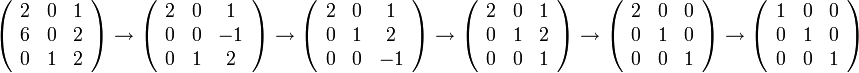
$\left(\begin{array}{ccc} 2 & 0 & 1 \\ 6 & 0 & 2 \\ 0 & 1 & 2 \end{array}\right)\to\left(\begin{array}{ccc} 2 & 0 & 1\\ 0 & 0 & -1\\ 0 & 1 & 2 \end{array}\right)\to\left(\begin{array}{ccc} 2 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & -1 \end{array}\right)\to\left(\begin{array}{ccc} 2 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{array}\right)\to\left(\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)\to\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)$

כלומר התשובה היא שלמערכת אין פתרון לא טריאלי. כלומר 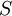$S$ בת"ל

משפט

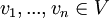$v_1,...,v_n\in V$ ת"ל אם"ם אחד מהוקטורים הינו צירוף לינארי של האחרים

הוכחה

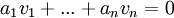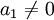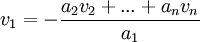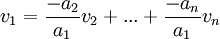הוקטורים ת"ל אם"ם קיימים סקלרים כך ש $a_1v_1+...+a_nv_n=0$ , ולפחות אחד מבין הסקלרים שונה מאפס. נניח ב.ה.כ. (בלי הגבלת הכלליות) ש $a_1\neq 0$ . לכן $v_1=-\frac{a_2v_2+...+a_nv_n}{a_1}$ ולכן $v_1=\frac{-a_2}{a_1}v_2+...+\frac{-a_n}{a_1}v_n$ .

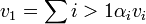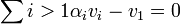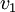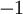בכיוון הפוך נניח כי (ב.ה.ב) הוקטור הראשון $v_1=\sum{i>1}\alpha_i v_i$ הוא צ"ל של האחרים. אזי $\sum{i>1}\alpha_i v_i-v_1=0$ . כלומר קיבלנו צ"ל שמתאפס שיש מקדם אחד לפחות ששונה מאפס (המקדם של $v_1$ הוא $-1$ ) על פי הגדרה הוקטורים ת"ל

שימו לב שיצא לנו שהוקטור הראשון תמיד צ"ל של האחרים, כמובן שזה לא נכון. זה נובע רק מטיעון ב.ה.כ שלנו, קל למצוא דוגמאות בהן הוקטור הראשון אינו צ"ל של האחרים.

ממשפט זה קל לנו לראות שהצלחנו בהגדרה שלנו לתלות:

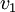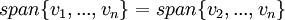מסקנה: אם $v_1$ הינו צירוף לינארי של האחרים ניתן להסיר אותו במובן הבא: $span\{v_1,...,v_n\}=span\{v_2,...,v_n\}$ .

תרגיל - הקשר בין צירוף לינארי לבין פתרון מערכת משוואות לינאריות

הוכח:

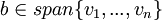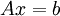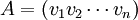$b\in span\{v_1,...,v_n\}$ אם"ם קיים פתרון למערכת $Ax=b$ כאשר $A=(v_1 v_2 \cdots v_n)$ הינה המטריצה שעמודותיה הן הוקטורים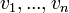 $v_1,...,v_n$

במקרה זה הפתרון x הינו וקטור הסקלרים של הצירוף הלינארי שנותן את b. כלומר, כאשר 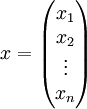$x=\begin{pmatrix}x_1\\x_2\\ \vdots \\ x_n\end{pmatrix}$ מתקיים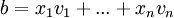 $b=x_1v_1+...+x_nv_n$

נניח והוקטורים שייכים למרחב 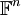$\mathbb{F}^n$ . הוכח שקיים צירוף לינארי יחיד הנותן את b אם"ם המטריצה הינה הפיכה. מה ניתן להסיק על הוקטורים במקרה זה?

פתרון

לפי כפל עמודה נכון לאמר ש 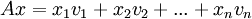$Ax=x_1v_1+x_2v_2+...+x_nv_n$ . לפיכך, ברור שקיים פתרון למערכת Ax=b אם"ם קיימים סקלרים כך ש 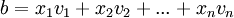$b=x_1v_1+x_2v_2+...+x_nv_n$ . אמנם התרגיל הזה טריוויאלי למדי אך חשוב מאד לזכור תוצאה זו, היא תשמש אותנו בהמשך רבות. בניסוח קליט: Ax הינה צירוף לינארי של עמודות A עם הסקלרים מ-x.

הוכחנו כבר בסעיף קודם.

אם הוקטורים שייכים למרחב 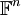$\mathbb{F}^n$ יוצא שהמטריצה הינה ריבועית וידוע שיש במקרה זה פתרון יחיד למערכת אם"ם המטריצה הפיכה. אם נציב b=0 ניתן להסיק מכך שלמערכת ההומוגנית יש פתרון יחיד אם"ם המטריצה הפיכה. למערכת ההומוגנית יש פתרון יחיד אם"ם הצירוף הלינארי היחיד של הוקטורים שמתאפס הינו הצירוף הלינארי הטריוויאלי (אפסים) ולכן המטריצה הפיכה אם"ם העמודות שלה בת"ל. מכיוון שאנו יודעים שמטריצה הפיכה אם"ם המשולחפת שלה הפיכה, ניתן גם להסיק שמטריצה הינה הפיכה אם"ם שורותיה בת"ל.

בסיס ומימד

תארנו את ההגדרה של תלות לינארית בתור היכולת לזרוק וקטורים מבלי להשפיע על המרחב הנפרש. כמובן שלפעולה זו יש סוף - מתישהו לא ניתן לזרוק אף וקטור מבלי לגרוע מהמרחב הנפרש. הקבוצה שנשארנו איתה במקרה זה תקרא בסיס.

הגדרה: יהי מרחב או תת מרחב W ותהי קבוצת וקטורים S. אזי S נקראת בסיס לW אם מתקיימות שתי התכונות הבאות:

S פורשת את W. כלומר, spanS=W.
S בת"ל. (כלומר, זרקנו ממנה את כל הוקטורים המיותרים.)

משפט: לכל מרחב וקטורי קיים בסיס, וכל הבסיסים לאותו המרחב הם מאותו גודל (כלומר, יש בהם אותו מספר ווקטורים).

לכן מותר להגדיר את ההגדרה הבאה:

הגדרה: יהיה מרחב וקטורי. ניקח לו בסיס כלשהו (מותר לפי המשפט), מספר האיברים בבסיס מוגדר להיות המימד של הבסיס. לא יכולה להיות סתירה בהגדרה מכיוון שלפי המשפט כל בסיס שנבחר ייתן בדיוק את אותו המספר.

הגדרה: הבסיס של מרחב האפס הינו הקבוצה הריקה, ולכן המימד של מרחב האפס הינו אפס.

(חידה מטופשת: אם ניקח את המימד של צירוף לינארי נקבל מנה טעימה. מהי?)

תרגיל

הוכח כי כל קבוצה A המכילה את אפס הינה תלויה לינארית

הוכחה

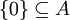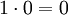יש למצוא קבוצה סופית של וקטורים ת"ל בתוך הקבוצה: $\{0\}\subseteq A$ . וקטור האפס תמיד תלוי לינארית כי לכל סקלר שונה מאפס (ובפרט לאחד) מתקיים $1\cdot 0 = 0$ .

לכן הקבוצה 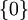$\{0\}$ לעולם אינה מהווה בסיס כי היא ת"ל, בפרט היא לא בסיס למרחב האפס.

משפט השלישי חינם

יהיה V מ"ו ותהי S קבוצה המוכלת בV. אזי אם שניים מבין התנאים הבאים מתקיימים, השלישי מתקיים בהכרח (בחינם) ומתקיים שS היא בסיס לV:

S בת"ל
spanS=V
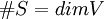מספר האיברים בS שווה למימד של V. (מסומן: $\#S=dimV$ .)

תרגיל חשוב (חלק מ7.7)

יהיה V מרחב וקטורי, ויהי W תת מרחב. הוכח/הפרך: אם dimV=dimW מתקיים שV=W בהכרח

פתרון

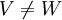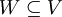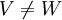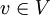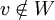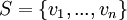נתון שdimV=dimW. נניח בשלילה ש $V\neq W$ ונראה אם אנחנו מקבלים סתירה או האם מוצאים דוגמא נגדית. מכיוון שנתון $W\subseteq V$ העובדה ש $V\neq W$ גוררת בהכרח שקיים וקטור $v\in V$ כך ש $v\notin W$ (זה תרגיל לוגי פשוט). נסמן dimW=dimV=n וניקח בסיס כלשהו לW (אנחנו יודעים שקיים כזה) $S=\{v_1,...,v_n\}$ .

כעת, נוכיח ש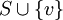 $S\cup \{v\}$ בהכרח בת"ל. נניח בשלילה שהיא כן תלוייה, לכן יש צירוף לינארי לא טריוויאלי של 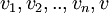$v_1,v_2,..,v_n,v$ שמתאפס. נניח והמקדם של v שונה מאפס, לכן קל להראות שהוא צירוף לינארי של האחרים בסתירה לכך ש-v אינו שייך לW (הרי יש סגירות בW לצירופים לינאריים) לכן המקדם של v הינו אפס. כעת נשארנו עם צירוף לינארי לא טריוויאלי שמתאפס של 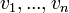$v_1,...,v_n$ וזו סתירה לכך שהם בת"ל מתוקף הגדרתם כבסיס.

על כן, מצאנו קבוצה בת"ל המכילה n+1 וקטורים, בסתירה לכך שהמימד של W הוא n.

התוצאה של תרגיל זה, כאמור, חשובה מאד. אם W תת מרחב של V והוכחנו שהם מאותו המימד זה מספיק על מנת להגיד שהם שווים. אתם תדרשו בעצם לעשות הוכחות כאלה באמצעות מימדים לא פעם ואף לא פעמיים.

תרגיל 7.17

יהא V מ"ו, ותהא B קבוצה המוכלת בV. הוכח שהתנאים הבאים שקולים:

B בסיס עבור V
וקטור האפס אינו שייך לB ולכל קבוצה 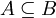$A\subseteq B$ מתקיים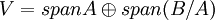 $V=spanA\oplus span(B/A)$

הוכחה

ראשית נוכיח שהתנאי הראשון גורר את השני:

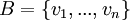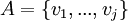נניח B בסיס לV, ברור מכך שB בת"ל שהוא אינו מכיל את אפס. תהי A קבוצה המוכלת בB נסמן ב.ה.כ $B=\{v_1,...,v_n\}$ ו $A=\{v_1,...,v_j\}$ . יש להוכיח בעצם שמתקיים 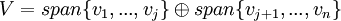$V=span\{v_1,...,v_j\}\oplus span\{v_{j+1},...,v_n\}$ . לצורך זה יש להוכיח שני דברים:

$span\{v_1,...,v_j\}\cap span\{v_{j+1},...,v_n\}=\{0\}$
$V=span\{v_1,...,v_j\}+ span\{v_{j+1},...,v_n\}$

(שימו לב שאם A ריקה, המשפט נובע בקלות ולכן לא נתייחס עוד למקרה קצה זה.)

נניח בשלילה שהתנאי הראשון אינו נכון, לכן קיים בחיתוך וקטור שונה מאפס. כלומר קיימים סקלרים כך ש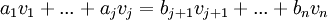 $a_1v_1+...+a_jv_j=b_{j+1}v_{j+1}+...+b_nv_n$ . מכיוון שמשני צידי המשוואה יש וקטור שונה מאפס, לפחות אחד מהסקלרים שונה מאפס. נעביר אגף ונקבל סתירה לכך שB בת"ל.

כעת, ברור שהמרחב כולו שווה לסכום הזה מכיוון שהמרחב מורכב מצירופים לינאריים של B והסכום הזה שווה בדיוק לכל הצירופים הלינאריים של B. (למעשה זה נובע מהתכונה הבאה: לכל שתי קבוצות A,B מתקיים: 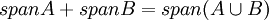$spanA+spanB=span(A \cup B)$ )

נוכיח שהתנאי השני גורר את הראשון:

מכיוון שזה נכון לכל קבוצה A המוכלת בB, בפרט זה נכון לקבוצה הריקה. לכן יוצא ש 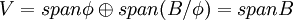$V=span\phi\oplus span (B/\phi)=spanB$ כלומר B פורש את V. נותר להראות שB בת"ל.

נניח בשלילה שB אינה בת"ל, לכן וקטור אחד ממנה u הוא צירוף לינארי של האחרים. נסמן בA את הנקודון שמכיל את u כלומר 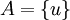$A=\{u\}$ ומכייון שבהכרח 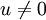$u \neq 0$ נקבל סתירה לתכונת הסכום הישר (חיתוך שכולל רק את ווקטור האפס)

משפט המימדים

משפט המימדים:

יהי V מ"ו ויהיו U,W תתי מרחבים. אזי 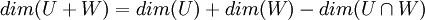$dim(U+W)=dim(U)+dim(W)-dim(U\cap W)$

סקיצה של ההוכחה - לא מפחיד כמו שנהוג לחשוב

ניקח בסיס לU חיתוך W. נסמן אותו ב $\{v_1,...,v_k\}$
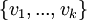
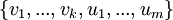
נשלים אותו לבסיס לU. נסמן $\{v_1,...,v_k,u_1,...,u_m\}$
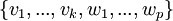
נשלים את הבסיס לחיתוך גם לבסיס לW. נסמן $\{v_1,...,v_k,w_1,...,w_p\}$
נוכיח (וזה עיקר העבודה) שהקבוצה 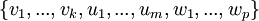הינה בסיס לU+W:
1. נראה כי כל וקטור מהצורה u+w ניתן להצגה כצירוף לינארי של איברים אלה (זה ברור)
2. נראה כי הקבוצה הזו בת"ל, אחרת וקטורים שהנחנו שאינם בחיתוך יהיו חייבים להיות בחיתוך בסתירה
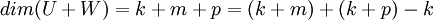
המשל נובע בקלות מספירת הוקטורים בבסיסים שכן $dim(U+W) = k+m+p=(k+m)+(k+p) -k$

תרגיל 8.3

יהא V מ"ו ממימד 5, ויהיו U ממימד 3 ו-W ממימד 4 תתי מרחבים של V. מהן האפשרויות עבור 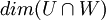$dim(U\cap W)$ ? הוכח!

פתרון

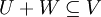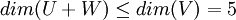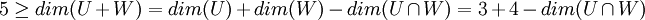ראשית, $U+W\subseteq V$ ולכן $dim(U+W)\leq dim(V)=5$ . אבל לפי משפט המימדים מתקיים $5\geq dim(U+W)=dim(U)+dim(W)-dim(U\cap W)=3+4-dim(U\cap W)$ .

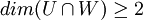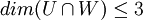ביחד מקבלים ש $dim(U\cap W)\geq 2$ . מצד שני, החיתוך מוכל גם בU וגם בW ולכן המימד שלו קטן שווה מהמימדים שלהם, ובפרט מהקטן מהם. לכן $dim(U\cap W)\leq 3$ .

סה"כ האפשרויות למימד הן 2,3. קל למצוא דוגמאות המוכיחות שאפשרויות אלה אכן מתקבלות מתישהו.

תרגיל 8.5

יהא V מ"ו ממימד n, ויהיו U,W תתי מרחבים כך ש dimU=n-1 ו-W אינו מוכל בU. הוכח כי W+U=V

הוכחה

נוכיח בעזרת משפט המימדים ש dim(U+W)=dimV ואז המשל נובע.

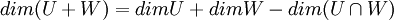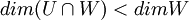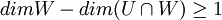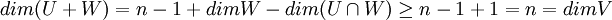$dim(U+W)=dimU+dimW-dim(U\cap W)$ . מכיוון שW אינו מוכל בU החיתוך בינהם שונה מW. ולכן $dim(U\cap W)<dimW$ ולכן $dimW-dim(U\cap W)\geq 1$ . ביחד מקבלים $dim(U+W)=n-1 + dimW -dim(U\cap W)\geq n-1+1=n=dimV$ . משל.

@@ שורה 52: / שורה 52: @@
 ===תרגילים===
+====תרגיל 1 ====
+במרחב הוקטורי <math>V=\mathbb{R}^{2}</math> מעל <math>\mathbb{R}</math> נגדיר
+<math>S=\{\left(\begin{array}{c}
+\\
+\end{array}\right),\left(\begin{array}{c}
+\\
+\end{array}\right),\left(\begin{array}{c}
+-2\\
+\end{array}\right)\}</math>
+מצא עבור אילו <math>a,b\in\mathbb{R}</math> מתקיים כי
+<math>\left(\begin{array}{c}
+a\\
+b
+\end{array}\right)\in span(S)
+</math>
+=====פתרון =====
 ==תלות לינארית==

הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/5"

גרסה מ־17:24, 12 ביולי 2015

תוכן עניינים

צירופים לינאריים והמרחב הנפרש (span)

תכונות

תרגילים

תרגיל 1

פתרון

תלות לינארית

דוגמאות

דוגמא 1

דוגמא 2

דוגמא 3

דוגמא 4

משפט

הוכחה

תרגיל - הקשר בין צירוף לינארי לבין פתרון מערכת משוואות לינאריות

פתרון

בסיס ומימד

תרגיל

הוכחה

משפט השלישי חינם

תרגיל חשוב (חלק מ7.7)

פתרון

תרגיל 7.17

הוכחה

משפט המימדים

סקיצה של ההוכחה - לא מפחיד כמו שנהוג לחשוב

תרגיל 8.3

פתרון

תרגיל 8.5

הוכחה

תפריט הניווט

חיפוש