88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 1.5
תוכן עניינים
רעיון בסיסי - אינדוקציה על הטבעיים
בשביל להוכיח שטענה מסוימת 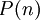 נכונה עבור כל מספר טבעי
(למשל
נכונה עבור כל מספר טבעי
(למשל 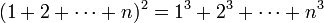 ) מספיק להוכיח את הבאים:
) מספיק להוכיח את הבאים:
- (בסיס האינדוקציה) הטענה מתקיימת עבור
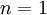 כלומר
כלומר 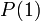 מתקיים
מתקיים - (צעד האינדוקציה)אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר
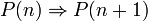 .
.
למה זה מספיק?
בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור 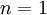 כלומר
כלומר 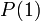 מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור
מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור 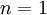 (שזה אכן כך) אז הטענה נכונה גם עבור
(שזה אכן כך) אז הטענה נכונה גם עבור 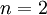 כלומר
כלומר 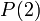 . אה! אז עכשיו זה נכון עבור
. אה! אז עכשיו זה נכון עבור 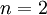 אז לפי אותה טענה זה נכון גם עבור
אז לפי אותה טענה זה נכון גם עבור 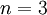 ! ומה עכשיו? אם זה נכון עבור
! ומה עכשיו? אם זה נכון עבור 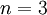 זה נכון עבור
זה נכון עבור 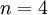 . וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר
. וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר 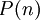 נכון לכל
נכון לכל 
דוגמא
נוכיח באינדוקציה כי הטענה 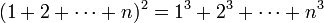 נכונה לכל
נכונה לכל 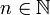 טבעי
טבעי
הוכחה:
עבור 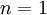 אכן מתקיים כי
אכן מתקיים כי 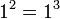
כעת נראה שאם הטענה נכונה עבור  כלשהוא, כלומר אם מתקיים
כלשהוא, כלומר אם מתקיים
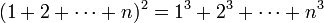 אזי הטענה נכונה עבור
אזי הטענה נכונה עבור  , כלומר
, כלומר
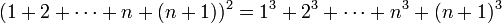 . כלומר נוכיח ש:
. כלומר נוכיח ש: 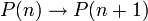
נוכיח:
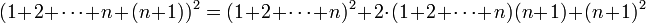
לפי הנחת האינדוקציה אפשר להמשיך הלאה
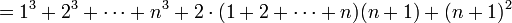
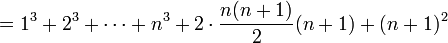
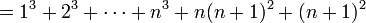
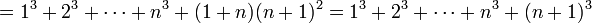
וסיימנו
דוגמא
הוכח כי לכל מספר טבעי  מתקיים כי
מתקיים כי 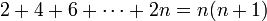
פתרון:
עבור 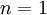 אכן מתקיים
אכן מתקיים 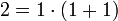
כעת נניח שהטענה נכונה עבור  ונוכיח את הטענה עבור
ונוכיח את הטענה עבור 
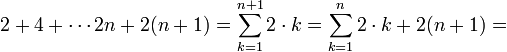
לפי הנחת האינדוקציה ניתן להמשיך
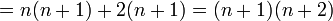
שזה הטענה עבור  וסיימנו.
וסיימנו.
תרגיל
הוכיחו שלכל  טבעי מתקיים
טבעי מתקיים 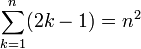
לפעמים כדאי להניח הנחות חזקות יותר
תרגיל:
נגדיר 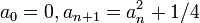 .
.
הוכח כי לכל n מתקיים 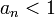
פתרון: נוכיח משהו יותר חזק - לכל n מתקיים 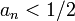
אכן: עבור 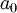 זה מתקיים. כעת נניח שנכון עבור n ונראה עבור n+1
זה מתקיים. כעת נניח שנכון עבור n ונראה עבור n+1
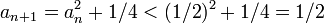
הכללות
הכללה פשוטה 1
הכללה ישירה מתבצעת כך (החלפה רק של הטענה הראשונה): אם נוכיח עבור טענה 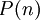 ש:
ש:
- הטענה מתקיימת עבור
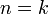 מסוים כלומר
מסוים כלומר 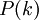 מתקיים
מתקיים - אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר
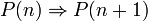 .
.
אז באופן דומה הטענה נכונה 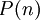 נכונה עבור
נכונה עבור 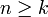
כלומר - במקום להוכיח עבור 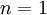 ואז הטענה מתקיים החל מ-1 ניתן להוכיח עבור
ואז הטענה מתקיים החל מ-1 ניתן להוכיח עבור 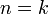 ואז הטענה מתקיים החל מ-k
ואז הטענה מתקיים החל מ-k
דוגמא:
הוכח כי לכל 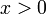 מתקיים
מתקיים 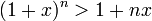 לכל
לכל 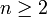
פתרון:
עבור 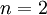 נקבל
נקבל 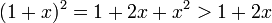 .
.
כעת נניח כי הטענה נכונה עבור  כלשהוא, כלומר מתקיים
כלשהוא, כלומר מתקיים 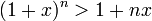
נוכיח עבור  מהנחת האינדוקציה נקבל כי
מהנחת האינדוקציה נקבל כי
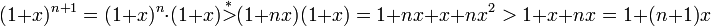
כאשר המעבר 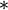 נובע מכך ש-
נובע מכך ש- 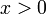 .
.
וסיימנו
תרגיל
מצאו עבור אילו  ים מתקיים
ים מתקיים 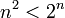
הכללה פשוטה 2
אם נוכיח עבור טענה 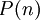 ש:
ש:
- הטענה מתקיימת עבור
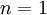 מסוים כלומר
מסוים כלומר 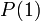 מתקיים
מתקיים - אם הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים
 (כלומר מתקיים
(כלומר מתקיים 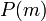 עבור
עבור 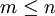 ) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר
) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר 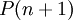 מתקיים).
מתקיים).
אז באופן דומה הטענה נכונה 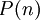 נכונה עבור
נכונה עבור 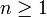
כלומר - אפשר להחליף את ההנחה שמתקיים עבור  ולהוכיח עבור
ולהוכיח עבור  בהנחה שמתקיים עבור כל מי שקטן שווה
בהנחה שמתקיים עבור כל מי שקטן שווה  ולהוכיח עבור
ולהוכיח עבור 
דוגמא:
כל מספר טבעי 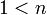 ניתן להציגו כמכפלה של מספרים ראשוניים
ניתן להציגו כמכפלה של מספרים ראשוניים
הוכחה:
עבור 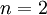 זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו.
זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו.
כעת נניח שהטענה נכונה לכל 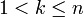 ונוכיח עבור
ונוכיח עבור 
אם  ראשוני - סיימנו כי אז הוא הפירוק של עצמו.
ראשוני - סיימנו כי אז הוא הפירוק של עצמו.
אחרת  מתפרק למכפלה
מתפרק למכפלה 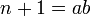 כאשר
כאשר 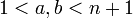 לפי הנחת האינדוקציה
לפי הנחת האינדוקציה 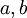 מתפרקים למכפלה של מספרים ראשוניים
מתפרקים למכפלה של מספרים ראשוניים
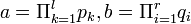 כאשר
כאשר 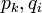 ראשוניים
ראשוניים
ואז 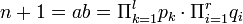
וסיימנו
עוד תרגילים מכינה למתמטיקה קיץ תשעב/תרגילים/4
מדריך אינדוקציה של מכון ויצמן
תרגילים יותר מעניינים (לא בסגנון "בני גורן". אם יש את הרקע המספק)
תרגיל
יהא  פסוק. נגדיר בעזרת אינדוקציה פסוקים:
פסוק. נגדיר בעזרת אינדוקציה פסוקים:
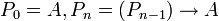 הוכיחו כי
הוכיחו כי 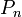 טואוטולוגיה כאשר
טואוטולוגיה כאשר  אי-זוגי.
אי-זוגי.
פתרון: נוכיח באינדוקציה כי לכל  אי-זוגי, הפסוק
אי-זוגי, הפסוק 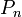 הוא טואוטולוגיה.בדיקה: עבור
הוא טואוטולוגיה.בדיקה: עבור 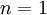 , הפסוק הוא
, הפסוק הוא 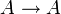 . הוא אכן טואוטולוגיה.
. הוא אכן טואוטולוגיה.
צעד: כעת, נניח את נכונות הטענה עבור  אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר
אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר 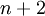 .
.
מתקיים: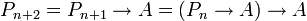 נראה כי זו אכן טואוטולוגיה. ראשית, לפי ההנחה,
נראה כי זו אכן טואוטולוגיה. ראשית, לפי ההנחה, 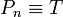 לכל ערך של
לכל ערך של  .
.
• אם 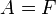 , נקבל
, נקבל 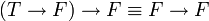 - אכן אמת.
- אכן אמת.
• אם 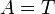 , נקבל
, נקבל 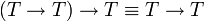 - אכן אמת.
- אכן אמת.
וסיימנו באינדוקציה.
תרגיל:
יהיו 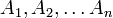 קבוצות אזי
קבוצות אזי 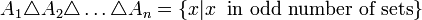
הוכחה:
עבור 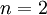 זה נכון כי הפרש סימטרי של 2 קבוצות זה כל ה
זה נכון כי הפרש סימטרי של 2 קבוצות זה כל ה  - ים שנמצאים או בראשונה בלבד או בשניה בלבד.
- ים שנמצאים או בראשונה בלבד או בשניה בלבד.
נניח כי הטענה נכונה עבור  קבוצות. נוכיח עבור
קבוצות. נוכיח עבור  קבוצות:
קבוצות:
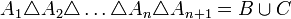 כאשר עיבוד הנוסחה נכשל (שגיאת תחביר): B=\{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\backslash A_{n+1} \} = \{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \land x\not\in A_{n+1} \} , \; \\ C= \{ x \; | \; x \in A_{n+1} \backslash (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \} = \{x \; | \; x \in A_{n+1} \land x\not\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\}
כאשר עיבוד הנוסחה נכשל (שגיאת תחביר): B=\{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\backslash A_{n+1} \} = \{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \land x\not\in A_{n+1} \} , \; \\ C= \{ x \; | \; x \in A_{n+1} \backslash (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \} = \{x \; | \; x \in A_{n+1} \land x\not\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\}
לפי הנחת האינדוקציה מתקיים 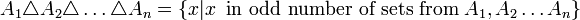 ולכן ניתן להמשיך כך
ולכן ניתן להמשיך כך
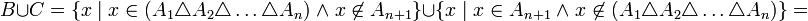
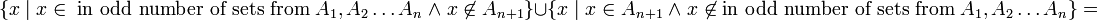
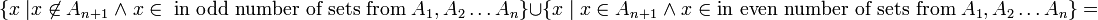
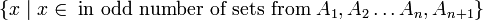
לכן, הטענה נכונה גם עבור  וסיימנו
וסיימנו
תרגיל
יהא  מספר ממשי המקיים כי
מספר ממשי המקיים כי 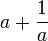 מספר שלם. הוכיחו כי לכל
מספר שלם. הוכיחו כי לכל  טבעי מתקיים כי
טבעי מתקיים כי 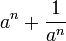 מספר שלם.
מספר שלם.
תרגיל
לכל  טבעי מתקיים: כל טבלה ריבועית בגודל
טבעי מתקיים: כל טבלה ריבועית בגודל 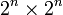 שהוצאנו ממנה משבצת, ניתן לכסות ב "י" (3 משבצות בצורת האות יוד)
שהוצאנו ממנה משבצת, ניתן לכסות ב "י" (3 משבצות בצורת האות יוד)
הוכחה: באינדוקציה.
בסיס  : טבלה ריבועית בגודל 2 על 2, ואכן כל משבצת שנוציא נשאר עם צורה "יוד" בודדת.
: טבלה ריבועית בגודל 2 על 2, ואכן כל משבצת שנוציא נשאר עם צורה "יוד" בודדת.
צעד: נניח נכונות עבור  ונוכיח נוכונות עבור
ונוכיח נוכונות עבור  . תהא טבלה בגודל
. תהא טבלה בגודל 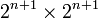 שהוצאנו משבצת. את הטבלה הזאת נחלק ל 4 טבלאות קטנות יותר בגודל
שהוצאנו משבצת. את הטבלה הזאת נחלק ל 4 טבלאות קטנות יותר בגודל 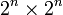 שאחת מהן חסרה משבצת. את הטבלה הזאת ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה. בנוסף ניתן להוציא "יוד" נוספת כך ששלושת הטבלאות האחרות יהיו חסרות משבצת אחת בדיוק ואז גם אותם ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה.
שאחת מהן חסרה משבצת. את הטבלה הזאת ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה. בנוסף ניתן להוציא "יוד" נוספת כך ששלושת הטבלאות האחרות יהיו חסרות משבצת אחת בדיוק ואז גם אותם ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה.
מסקנה: לכל  טבעי מתקיים ש 3 מחלק את
טבעי מתקיים ש 3 מחלק את 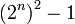 .
.
תרגיל
תהא טבלת שוקולד עם 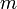 שורות ו
שורות ו  עמודות. חיתוך של טבלת שוקולד הוא שבירת הטבלה לשתי טבלאות קטנות לאורך או לרוחב הטבלה המקורית. הוכיחו כי בהינתן טבלה עם
עמודות. חיתוך של טבלת שוקולד הוא שבירת הטבלה לשתי טבלאות קטנות לאורך או לרוחב הטבלה המקורית. הוכיחו כי בהינתן טבלה עם 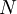 קוביות שוקולד, צריך בדיוק
קוביות שוקולד, צריך בדיוק 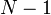 חיתוכים על מנת להפריד כל קוביה בנפרד (כלומר לקבל
חיתוכים על מנת להפריד כל קוביה בנפרד (כלומר לקבל 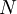 טבלאות שכל אחת מגודל 1 על 1).
טבלאות שכל אחת מגודל 1 על 1).
הוכחה: באינדוקציה שלמה. אם הטבלה בגודל 1 על 1 סיימנו. אחרת, נבצע חיתוך שרירותי, נקבל 2 טבלאות קטנות יותר, נפעיל עליהם את הנחת האינדוקציה וסיימנו.
תרגיל
הוכיחו בעזרת אינדוקציה כי כל מצולע קמור (כלומר הצלע בין כל שני קודקודים נמצאת בפנים המצולע) בן 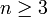 צלעות ניתן לשילוש (כלומר ניתן לחלק אותו למשולשים)
ושיש בשילוש
צלעות ניתן לשילוש (כלומר ניתן לחלק אותו למשולשים)
ושיש בשילוש 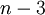 אלכסונים.
אלכסונים.
פתרון:
עבור 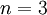 : מצולע קמור בן 3 צלעות חייב להיות משולש (ייתכן בעיוות כלשהוא) ולכן הוא ניתן לשילוש ע"י
: מצולע קמור בן 3 צלעות חייב להיות משולש (ייתכן בעיוות כלשהוא) ולכן הוא ניתן לשילוש ע"י
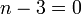 אלכסונים.
אלכסונים.
כעת נניח שהטענה נכונה עבור כל מצולע קמור בן 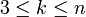 ונוכיח את הטענה עבור מצלוע קמור בן
ונוכיח את הטענה עבור מצלוע קמור בן  צלעות (כלומר שכל מצולע קמור בן
צלעות (כלומר שכל מצולע קמור בן  ניתן לשילוש עם
ניתן לשילוש עם 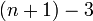 אלכסונים). יהא מצולע קמור
אלכסונים). יהא מצולע קמור 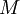 בן
בן  צלעות. נמתח קו בין שני קודקודים שלו. כעת המצולע שהתחלנו איתו התחלק לשני מצולעים קמורים, נסמנם
צלעות. נמתח קו בין שני קודקודים שלו. כעת המצולע שהתחלנו איתו התחלק לשני מצולעים קמורים, נסמנם 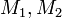 . נסמן את מספר הצלעות של
. נסמן את מספר הצלעות של 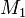 ב
ב  (כלומר יש לו
(כלומר יש לו 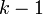 צלעות משותפות עם
צלעות משותפות עם 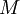 + הצלע שהוספנו. מספר הצלעות של
+ הצלע שהוספנו. מספר הצלעות של 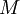 הוא
הוא  ולכן מספר הצלעות המשותפות בין
ולכן מספר הצלעות המשותפות בין 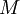 ל
ל 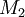 הוא
הוא
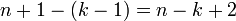 ולכן מספר הצלעות של
ולכן מספר הצלעות של 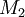 הוא
הוא 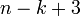 .
כיוון ש
.
כיוון ש 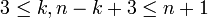 ניתן להפעיל את הנחת האינדוקציה על
ניתן להפעיל את הנחת האינדוקציה על 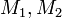 ולהסיק כי
ולהסיק כי 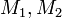 ניתן לשילוש ע"י
ניתן לשילוש ע"י 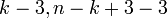 אלכסונים.
צירוף השילושים של
אלכסונים.
צירוף השילושים של 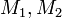 יתן שילוש של
יתן שילוש של 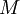 עם
עם 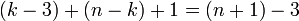 אלכסונים כנדרש.
אלכסונים כנדרש.
תרגיל:
יהיו 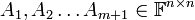 מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י הנוסחא
מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י הנוסחא
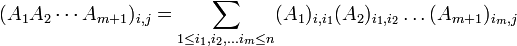
הוכחה (באינדוקציה על מספר המטריצות):
עבור 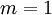 זה ההגדרה של כפל בין 2 מטריצות
זה ההגדרה של כפל בין 2 מטריצות
כעת, נניח שהטענה נכונה עבור 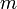 כל שהוא. נוכיח נכונות עבור
כל שהוא. נוכיח נכונות עבור 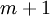
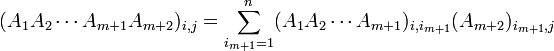
לפי הנחת האינדוקציה נמשיך:
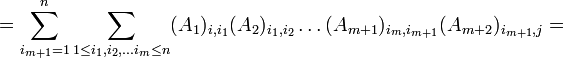
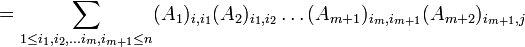
וסיימנו.
אזהרה
אינדוקציה היא כלי חזק אך יש לשים לב כי משתמשים בו נכונה.
דוגמא מפורסמת להוכחת שגויה באינדוקציה היא הדוגמא הבא:
טענה: כל קבוצה של סוסים לא ריקה מכילה סוסים מצבע יחיד.
"הוכחה": נוכיח בעזרת אינדוקציה על מספר האיברים בקבוצת הסוסים.
עבור 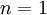 אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד
אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד
כעת נניח כל קבוצה עם  סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל
סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל 
תהא 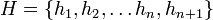 קבוצה עם
קבוצה עם  סוסים אזי לפי הנחת האינדוקציה
סוסים אזי לפי הנחת האינדוקציה
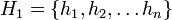 ו
ו 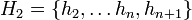 הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל
הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל  )
ולכן כל הסוסים ב
)
ולכן כל הסוסים ב 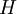 ג"כ בעלי צבע יחיד (כי יש חפיפה בין
ג"כ בעלי צבע יחיד (כי יש חפיפה בין 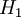 ובין
ובין 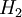 .
.
חישבו איפה השגיאה (רמז: במעבר מ 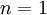 ל
ל 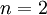 )
)
סדר טוב - העשרה מתקדמת ביותר, לא להעביר לשנה א
הגדרה: יהי  יחס סדר חלקי על קבוצה
יחס סדר חלקי על קבוצה  .
.
 יקרא סדר טוב אם לכל
יקרא סדר טוב אם לכל 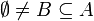 קיים איבר מינימום/הכי קטן/ראשון ב
קיים איבר מינימום/הכי קטן/ראשון ב  .
.
מינוח: נאמר כי  סדורה היטב.
סדורה היטב.
דוגמא: הקס"ח 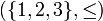 היא סדורה היטב - תתי הקבוצות הלא ריקות שלה הן
היא סדורה היטב - תתי הקבוצות הלא ריקות שלה הן 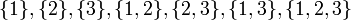 והאיבר הראשון בכל תת קבוצה הוא בהתאמה
והאיבר הראשון בכל תת קבוצה הוא בהתאמה 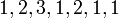 .
.
עקרון הסדר הטוב
נסתכל על 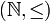 - קבוצת הטבעיים עם יחס הסדר "קטן שווה" הסטנדרטי.
- קבוצת הטבעיים עם יחס הסדר "קטן שווה" הסטנדרטי.
אינטואיטיבית, אכן מתקיים כי לכל קבוצה לא ריקה של טבעיים קיים איבר ראשון - "אם 1 שם, הוא הקטן ביותר; אם 2 שם, הוא הקטן ביותר; ממשיכים כך עד שמגיעים לאיבר כלשהו (כי הקבוצה לא ריקה), והוא הקטן ביותר".
פורמלית, טענה זו, הנקראת עקרון הסדר הטוב, והיא שקולה לטענת (/אקסיומת) האינדוקציה.
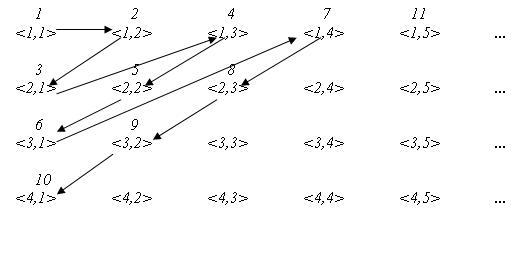
דוגמא נוספת: ניתן להגדיר אל 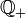 יחס סדר חלקי לפי התמונה הבא (כאשר מזהים כל שבר עם זוג סדור ומבטלים את החזרות המיותרות)
יחס סדר חלקי לפי התמונה הבא (כאשר מזהים כל שבר עם זוג סדור ומבטלים את החזרות המיותרות)
התבוננו והשתכנעו שזה גם סדר טוב.
הערה: זה בניגוד לסדר "קטן שווה" הרגיל על השברים שאינו סדר טוב כי לקבוצה
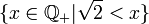 אין איבר מינימום.
אין איבר מינימום.
משפט הסדר הטוב
משפט הסדר הטוב קובע שלכל קבוצה  קיים סדר טוב.
קיים סדר טוב.
תרגיל:
תהא  קבוצה בת מנייה. הוכח כי ניתן לסדר אותה היטב (בהינתן עקרון הסדר הטוב).
קבוצה בת מנייה. הוכח כי ניתן לסדר אותה היטב (בהינתן עקרון הסדר הטוב).
פתרון:
לפי הנתון קיימת פונקציה חח"ע ועל 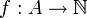 .
נגדיר את היחס הבא על
.
נגדיר את היחס הבא על  כך:
כך: 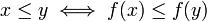 . זהו יחס סדר (השתכנעו!).
בנוסף,
. זהו יחס סדר (השתכנעו!).
בנוסף,  סדורה היטב על ידו: תהא
סדורה היטב על ידו: תהא 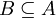 תת קבוצה לא ריקה. אזי
תת קבוצה לא ריקה. אזי 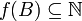 תת קבוצה לא ריקה ולכן קיים בה איבר מינימום נסמנו
תת קבוצה לא ריקה ולכן קיים בה איבר מינימום נסמנו  . בדקו כי
. בדקו כי
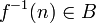 איבר מינימום.
איבר מינימום.
הכללה עקרון האינדוקציה בעזרת קבוצות סדורות היטב
תהא  קבוצה סדורה היטב (נסמן את היחס שלה ב
קבוצה סדורה היטב (נסמן את היחס שלה ב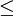 ) אזי:
) אזי:
- אם
![\forall n ([\forall m<n P(m)] \to P(n))](/images/math/f/4/b/f4b5ab9ea2d5cad7a28dc415a95828cc.png)
- אז
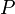 מתקיימת לכל
מתקיימת לכל 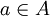
למה זה עובד?
נניח בשלילה כי הטענה 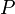 לא מתקיימת לכל
לא מתקיימת לכל 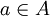 אזי נגדיר
אזי נגדיר 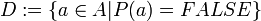 - קבוצת כל האיברים ב
- קבוצת כל האיברים ב  שעבורם הטענה אינה נכונה. מהנחת השלילה
שעבורם הטענה אינה נכונה. מהנחת השלילה 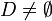 .
.
כיוון ש  סדורה היטב אזי קיים ב
סדורה היטב אזי קיים ב 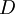 מינימום, נסמנו
מינימום, נסמנו 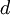 . לפי הגדרת מינימום והגדרת
. לפי הגדרת מינימום והגדרת 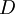 נובע כי לכל
נובע כי לכל 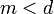 הטענה נכונה (אם היה
הטענה נכונה (אם היה 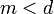 שהטענה לא נכונה לגביו אזי הוא היה בקבוצה
שהטענה לא נכונה לגביו אזי הוא היה בקבוצה 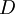 ואז זה היה סתירה לכך ש
ואז זה היה סתירה לכך ש 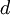 מינימום של קבוצה זאת).
מינימום של קבוצה זאת).
אבל אם זה כך אז לפי הטענה שמוכיחים זה גורר כי 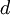 כן מתקיים. סתירה. ולכן הטענה נכונה לכל
כן מתקיים. סתירה. ולכן הטענה נכונה לכל 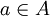
הערה: אפשר לעשות אינדוקציה הנקראת אינדוקציה טרנספניטית על קבוצות כלשהן (לאו דווקא בנות מניה)