הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 4"
אחיה בר-און (שיחה | תרומות) (←פונקציות) |
אחיה בר-און (שיחה | תרומות) (←פונקציות) |
||
| שורה 4: | שורה 4: | ||
'''הגדרה:''' יהיו A,B קבוצות וR יחס בינהן. אזי: | '''הגדרה:''' יהיו A,B קבוצות וR יחס בינהן. אזי: | ||
*התחום של R הינו <math>dom(R)=\{a\in A|\exists b\in B:(a,b)\in R\}=\{(*,\;),(*,\;)\dots \}</math> | *התחום של R הינו <math>dom(R)=\{a\in A|\exists b\in B:(a,b)\in R\}=\{(*,\;),(*,\;)\dots \}</math> | ||
| − | *התמונה של R הינה <math>im(R)=\{b\in B|\exists a\in A:(a,b)\in R\}</math> | + | *התמונה של R הינה <math>im(R)=\{b\in B|\exists a\in A:(a,b)\in R\}=\{(\;,*),(\; ,*)\dots \}</math> |
'''דוגמא.''' | '''דוגמא.''' | ||
*אם R יחס מלא על A אזי האיחוד של התמונה והתחום שווה A | *אם R יחס מלא על A אזי האיחוד של התמונה והתחום שווה A | ||
| − | *<math>R=\{(1,a),(2,b),(3,a)\}</math> אזי התחום הוא <math>dom(R)=\{1,2,3\}</math> והתמונה הינה <math>im(R)=\{a,b\}</math> | + | *<math>R=\{(1,a),(2,b),(3,a),(a,1)\}</math> אזי התחום הוא <math>dom(R)=\{a,1,2,3\}</math> והתמונה הינה <math>im(R)=\{1,a,b\}</math> |
'''הגדרה:''' | '''הגדרה:''' | ||
| − | |||
| − | |||
*יחס R נקרא '''על''' אם <math>\forall b\in B:\exists a\in A:(a,b)\in R</math> כלומר <math>im(R)=B</math> | *יחס R נקרא '''על''' אם <math>\forall b\in B:\exists a\in A:(a,b)\in R</math> כלומר <math>im(R)=B</math> | ||
| − | *יחס R מ-A ל-B נקרא '''שלם''' אם <math>\forall a\in A:\exists b\in B:(a,b)\in R</math> | + | *יחס R מ-A ל-B נקרא '''שלם''' אם <math>\forall a\in A:\exists b\in B:(a,b)\in R</math> כלומר <math>dom(R)=A</math> |
| + | *יחס R נקרא '''חד ערכי''' אם <math>[(x,b)\in R] \and [(x,d) \in R] \rightarrow (d=b)</math> כלומר אין איבר שנשלח ל-2 מקומות שונים | ||
| + | *יחס R נקרא '''חד-חד ערכי''' אם <math>[(x,b)\in R] \and [(y,b) \in R] \rightarrow (x=y)</math> כלומר איברים שונים נשלחים למקומות שונים (כלומר, היחס ההופכי הינו חד ערכי) | ||
| + | |||
'''הגדרה:''' | '''הגדרה:''' | ||
| − | יחס חד ערכי ושלם נקרא '''פונקציה'''; נסמן במקרה זה <math>(a,b)\in R\leftrightarrow b=R(a)</math>. | + | יחס חד ערכי ושלם נקרא '''פונקציה'''; נסמן במקרה זה <math>(a,b)\in R\leftrightarrow b=R(a)</math>. |
| + | ובאופן כללי <math>f:A\to B \;\; , a \mapsto f(a)</math>. | ||
| + | (A נקרא תחום הגדרה של הפונקציה.) | ||
'''דוגמאות:''' | '''דוגמאות:''' | ||
| שורה 31: | שורה 34: | ||
'''הוכחה.''' | '''הוכחה.''' | ||
| − | + | נסמן <math>f:A\to B, A=\{a_1,\dots a_n\},B=\{b_1,\dots b_n\} </math> . כאשר כל האיברים ב A שונים זה מזה וכנ"ל ל B | |
| − | נניח | + | נניח <math>f </math> חח"ע אזי <math>|\{f(a_1),\dots f(a_n)\}|=n</math> |
| + | כיוון ש <math>\{f(a_1),\dots f(a_n)\}\subseteq B </math> מתקיים שיוון ולכן <math>f </math> על. | ||
| − | + | נניח <math>f </math> על. נניח בשלילה ש <math>f </math> אינה חח"ע אזי <math>|\{f(a_1),\dots f(a_n)\}|<n</math> | |
| − | + | ואז <math>f </math> אינה על -סתירה. | |
| − | + | הערה: הדבר אינו נכון אם A וB קבוצות אינסופיות. | |
| − | + | ||
| + | למשל פונקצית הערך השלם על ואינה חח"ע | ||
| + | |||
| + | '''הגדרה:''' | ||
| + | יהיו <math>f:A\to B, g:B\to C </math> שתי פונקציות אזי ההרכבה שלהם <math>g \circ f:A\to C </math> | ||
| + | מוגדרת <math>g \circ f(a)=g(f(a)) </math> | ||
'''תרגיל.''' | '''תרגיל.''' | ||
גרסה מ־15:00, 23 ביולי 2013
פונקציות
הגדרה: יהיו A,B קבוצות וR יחס בינהן. אזי:
- התחום של R הינו
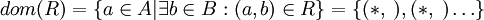
- התמונה של R הינה
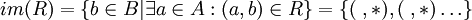
דוגמא.
- אם R יחס מלא על A אזי האיחוד של התמונה והתחום שווה A
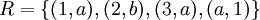 אזי התחום הוא
אזי התחום הוא 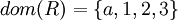 והתמונה הינה
והתמונה הינה 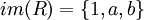
הגדרה:
- יחס R נקרא על אם
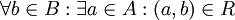 כלומר
כלומר 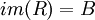
- יחס R מ-A ל-B נקרא שלם אם
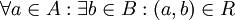 כלומר
כלומר 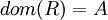
- יחס R נקרא חד ערכי אם
![[(x,b)\in R] \and [(x,d) \in R] \rightarrow (d=b)](/images/math/8/b/a/8ba1cf7695007d890739c921bba19ad7.png) כלומר אין איבר שנשלח ל-2 מקומות שונים
כלומר אין איבר שנשלח ל-2 מקומות שונים - יחס R נקרא חד-חד ערכי אם
![[(x,b)\in R] \and [(y,b) \in R] \rightarrow (x=y)](/images/math/7/9/3/793fbb6e03f69ce8b33496266443a246.png) כלומר איברים שונים נשלחים למקומות שונים (כלומר, היחס ההופכי הינו חד ערכי)
כלומר איברים שונים נשלחים למקומות שונים (כלומר, היחס ההופכי הינו חד ערכי)
הגדרה:
יחס חד ערכי ושלם נקרא פונקציה; נסמן במקרה זה 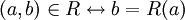 .
ובאופן כללי
.
ובאופן כללי 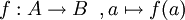 .
(A נקרא תחום הגדרה של הפונקציה.)
.
(A נקרא תחום הגדרה של הפונקציה.)
דוגמאות:
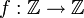 כאשר
כאשר 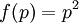 (אינה חח"ע ואינה על)
(אינה חח"ע ואינה על)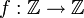 כאשר
כאשר 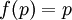 . זו נקראת פונקצית הזהות והיא חח"ע וגם על
. זו נקראת פונקצית הזהות והיא חח"ע וגם על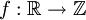 כאשר
כאשר ![f(x)=[x]](/images/math/d/0/a/d0a42349646d7ba0cdb154e28162cb95.png) מוגדר להיות הערך השלם הקרוב ביותר ל-x (במקרה של חצי לוקחים את הגבוה). זו פונקציה על שאינה חח"ע
מוגדר להיות הערך השלם הקרוב ביותר ל-x (במקרה של חצי לוקחים את הגבוה). זו פונקציה על שאינה חח"ע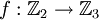 כאשר לוקחים את 0 ל0 ואת 1 ל1. זו פונקציה חח"ע שאינה על. (כל פונקציה היא על לתמונה של עצמה.)
כאשר לוקחים את 0 ל0 ואת 1 ל1. זו פונקציה חח"ע שאינה על. (כל פונקציה היא על לתמונה של עצמה.)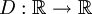 פונקצית דיריכליי: על כל מספר רציונאלי מקבלת 1 ועל כל מספר אי רציונאלי מקבלת אפס.
פונקצית דיריכליי: על כל מספר רציונאלי מקבלת 1 ועל כל מספר אי רציונאלי מקבלת אפס.
תרגיל. יהיו A וB קבוצות סופיות בעלות עוצמה זהה. הוכח שכל פונקציה מA לB הינה על אם"ם היא חח"ע
הוכחה.
נסמן 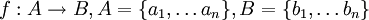 . כאשר כל האיברים ב A שונים זה מזה וכנ"ל ל B
. כאשר כל האיברים ב A שונים זה מזה וכנ"ל ל B
נניח  חח"ע אזי
חח"ע אזי 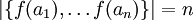 כיוון ש
כיוון ש 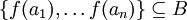 מתקיים שיוון ולכן
מתקיים שיוון ולכן  על.
על.
נניח  על. נניח בשלילה ש
על. נניח בשלילה ש  אינה חח"ע אזי
אינה חח"ע אזי 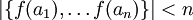 ואז
ואז  אינה על -סתירה.
אינה על -סתירה.
הערה: הדבר אינו נכון אם A וB קבוצות אינסופיות.
למשל פונקצית הערך השלם על ואינה חח"ע
הגדרה:
יהיו 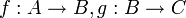 שתי פונקציות אזי ההרכבה שלהם
שתי פונקציות אזי ההרכבה שלהם 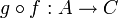 מוגדרת
מוגדרת 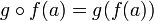
תרגיל.
- נניח
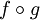 חח"ע. הוכח/הפרך: f חח"ע, g חח"ע
חח"ע. הוכח/הפרך: f חח"ע, g חח"ע - נניח
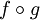 על. הוכח/הפרך: f על, g על
על. הוכח/הפרך: f על, g על
פתרון.
נניח 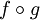 חח"ע. נניח בשלילה ש-g אינה חח"ע. לכן קיימים
חח"ע. נניח בשלילה ש-g אינה חח"ע. לכן קיימים 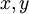 כך ש
כך ש 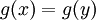 אבל
אבל 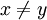 . אבל,
. אבל, 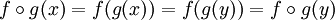 בסתירה לחח"ע של ההרכבה, ולכן g חח"ע.
בסתירה לחח"ע של ההרכבה, ולכן g חח"ע.
לגבי f ניתן דוגמא נגדית: 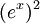
נניח 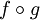 על. נסמן
על. נסמן 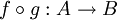 אזי לכל איבר
אזי לכל איבר 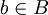 קיים איבר
קיים איבר 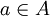 כך ש
כך ש 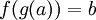 . לכן עבור f לכל b קיים
. לכן עבור f לכל b קיים 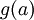 שנותן את b תחת f ולכן f על.
שנותן את b תחת f ולכן f על.
דוגמא נגדית ל g: נביט בפונקציות מהטבעיים לטבעיים. 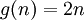 , והפונקציה f מוגדרת כ
, והפונקציה f מוגדרת כ 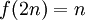 ו
ו 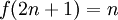 . ההרכבה הינה פונקצית הזהות שהיא בפרט על, אבל g אינה על כיוון שהאי זוגיים כלל לא נמצאים בתמונה שלה.
. ההרכבה הינה פונקצית הזהות שהיא בפרט על, אבל g אינה על כיוון שהאי זוגיים כלל לא נמצאים בתמונה שלה.
הגדרה: פונקצית הזהות על A הינה פונקציה מA לעצמו השולחת כל איבר לעצמו. נהוג לסמנה ב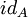 . פונקציה
. פונקציה 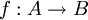 נקראת הפיכה אם קיימת לה הופכית - פונקציה
נקראת הפיכה אם קיימת לה הופכית - פונקציה 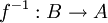 כך שמתקיים
כך שמתקיים 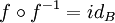 וגם
וגם 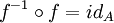 .
.
הערה: זכרו שפונקציה היא יחס. הפונקציה ההופכית שלה היא היחס ההופכי מטבע הדברים. על מנת שהיחס ההופכי יהיה פונקציה הוא צריך להיות ח"ע ושהתחום שלו יהיה כל B. תנאים אלה מתממשים רק אם f הינה חח"ע ועל.