הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 6"
(←עוצמות) |
(←עוצמות) |
||
| שורה 41: | שורה 41: | ||
אם נסתכל על קבוצה של קבוצות ניתן להגדיר עליה יחס "עוצמות שוות" והוא יהיה יחס רפלקסיבי, סימטרי וטרנזיטיבי. עם זאת, לא ניתן להגדיר יחס זה על כל הקבוצות כולם בשל הסיבה שלא קיימת קבוצת כל הקבוצות. | אם נסתכל על קבוצה של קבוצות ניתן להגדיר עליה יחס "עוצמות שוות" והוא יהיה יחס רפלקסיבי, סימטרי וטרנזיטיבי. עם זאת, לא ניתן להגדיר יחס זה על כל הקבוצות כולם בשל הסיבה שלא קיימת קבוצת כל הקבוצות. | ||
נראה שימוש בתכונות אלו בתרגילים הבאים. | נראה שימוש בתכונות אלו בתרגילים הבאים. | ||
| − | + | ||
| + | ===תרגיל === | ||
| + | תהא A קבוצה. הוכח כי <math>|A|\leq |P(A)|</math> | ||
| + | |||
| + | פתרון: נגדיר את הפונקציה <math>f:A|\to P(A)</math> ע"י <math>a \mapsto \{a\}</math> היא חח"ע. | ||
| + | |||
| + | ===תרגיל === | ||
| + | נגדיר <math>A=\{f: \{1,2,3\}\to \{1,2,3,4,5\} : f \text{ is a function}\}, B=\{(x,y,z): 1\leq x,y,z \leq 5\}</math> | ||
| + | |||
| + | הוכח כי A ו B שוות עוצמה | ||
| + | |||
| + | פתרון: | ||
| + | |||
== עוצמת הטבעיים == | == עוצמת הטבעיים == | ||
'''תרגיל.''' | '''תרגיל.''' | ||
גרסה מ־15:30, 27 ביולי 2015
תוכן עניינים
עוצמות
הגדרה. יהיו A,B שתי קבוצות. אזי:
- אם קיימת
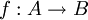 חח"ע ועל אז אומרים של A ולB יש אותה עוצמה (סימון
חח"ע ועל אז אומרים של A ולB יש אותה עוצמה (סימון 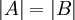 )
) - אם קיימת
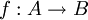 חח"ע אז אומרים כי העוצמה של A קטנה או שווה לזו של B. (סימון
חח"ע אז אומרים כי העוצמה של A קטנה או שווה לזו של B. (סימון 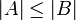 )
) - אם
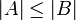 וגם
וגם 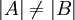 אזי אומרים כי העוצמה של A קטנה ממש מהעצמה של B (סימון
אזי אומרים כי העוצמה של A קטנה ממש מהעצמה של B (סימון 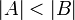 )
)
הערה: בעזרת אקסיומת הבחירה מוכיחים כי אם קיימת 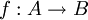 על אזי
על אזי 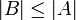 (בעזרת התרגיל מתירגול קודם כי ניתן לצמצם את התחום של f כך שתהא חח"ע)
(בעזרת התרגיל מתירגול קודם כי ניתן לצמצם את התחום של f כך שתהא חח"ע)
דוגמא. יהיו A וB שתי קבוצות סופיות. אזי אם מספר האיברים בהן שווה עוצמתן שווה, ואם מספר האיברים בA גדול מזה של B אזי עוצמתה של A גדולה יותר.
לכל קבוצה סופית בעלת n איברים, נאמר שעוצמתה הינה n. למשל 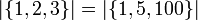
טענה. אם 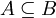 אזי
אזי 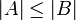 .
.
הוכחה: נגדיר 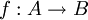 פונקצית ההכלה השולחת כל איבר לעצמו. פונקציה זו חח"ע ולכן
פונקצית ההכלה השולחת כל איבר לעצמו. פונקציה זו חח"ע ולכן 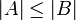
תרגיל הוכח כי עוצמת 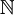 שווה ל -
שווה ל -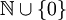
הוכחה: נגדיר 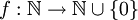 ע"י
ע"י 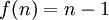 .
.
 חח"ע ועל כי יש לה הופכית
חח"ע ועל כי יש לה הופכית 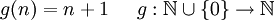
טענה. אם A קבוצה וR יחס שקילויות על הקבוצה אזי עוצמת קבוצת המנה קטנה או שווה לעוצמה של A.
הוכחה: נגדיר 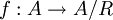 ע"י
ע"י ![f(a)=[a]_R](/images/math/7/e/1/7e1ee448a9e83d5245d6309678b2c07d.png) . הפונקציה על ולכן
. הפונקציה על ולכן 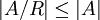
טענה אם 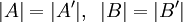 אזי
אזי 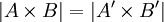
הוכחה: קיימות פונקציות חח"ע ועל 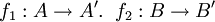
נגדיר פונקציה 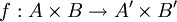 ע"י
ע"י 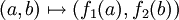 כיוון ש
כיוון ש 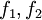 חח"ע ועל גם
חח"ע ועל גם  כזאת.
כזאת.
למשל 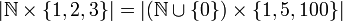
הערה אם נסתכל על קבוצה של קבוצות ניתן להגדיר עליה יחס "עוצמות שוות" והוא יהיה יחס רפלקסיבי, סימטרי וטרנזיטיבי. עם זאת, לא ניתן להגדיר יחס זה על כל הקבוצות כולם בשל הסיבה שלא קיימת קבוצת כל הקבוצות. נראה שימוש בתכונות אלו בתרגילים הבאים.
תרגיל
תהא A קבוצה. הוכח כי 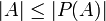
פתרון: נגדיר את הפונקציה 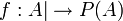 ע"י
ע"י 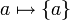 היא חח"ע.
היא חח"ע.
תרגיל
נגדיר 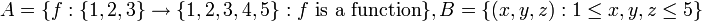
הוכח כי A ו B שוות עוצמה
פתרון:
עוצמת הטבעיים
תרגיל.
הוכח שעוצמות הקבוצות הבאות שוות: 
הוכחה: נבנה פונקציות חח"ע ועל ונוכיח מספר טענות עזר בדרך.
- נגדיר
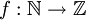 ע"י
ע"י
- אם n זוגי אזי
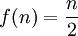
- אחרת,
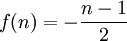
- אם n זוגי אזי
קל לוודא שפונקציה זו חח"ע ועל לכן עוצמת השלמים ועוצמת הטבעיים שווה.
טענה. מתקיים ש 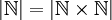 .
.
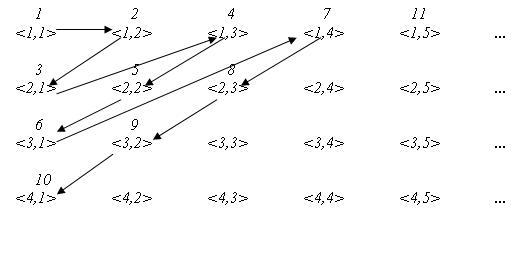
הוכחה. נביט באוסף הזוגות הסדורים של מספרים טבעיים, ונחלק אותם לקבוצות לפי סכום האיברים בזוג. בקבוצה הראשונה יהיה הזוג (1,1), בקבוצה השנייה יהיו הזוגות (1,2),(2,1), בקבוצה השלישית יהיו הזוגות (1,3),(2,2),(3,1) וכדומה.
נגדיר פונקציה 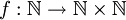 באופן הבא:
באופן הבא:
- 1 נשלח לזוג הראשון בקבוצה הראשונה
- 2 נשלח לזוג הראשון בקבוצה השנייה
- 3 נשלח לזוג השני בקבוצה השנייה
- 4 נשלח לזוג הראשון בקבוצה השלישית
- ...
קל לראות שפונקציה זו מוגדרת היטב. לכל מספר טבעי פשוט עוקבים אחרי התהליך הזה ורואים לאיזה זוג הוא נשלח. כמו כן, לכל זוג ניתן לעבור על התהליך עד שיגיע המספר שישלח אליו.
כמו כן קל לראות שפונקציה זו חח"ע וגם על.
משפט (קנטור- שרדר-ברנשטיין) אם 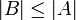 וגם
וגם 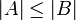 אז
אז 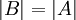
טענה. מתקיים ש 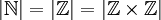 .
.
הוכחה: כיוון ש 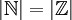 אזי לפי תרגיל ממקודם
אזי לפי תרגיל ממקודם
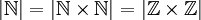
נזכר ש 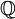 הם קבוצת מנה של
הם קבוצת מנה של  ולכן
ולכן
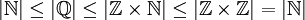
לפי קנטור ברנשטיין נקבל ש 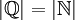
הגדרה
- העוצמה של הטבעיים מסומנת
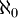
- קבוצה A המקיימת
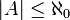 נקראת בת מנייה (מקור השם כי ניתן למנות/ למספר את האיברים בה ע"י התאמה חח"ע ועל מהטבעיים במקרה האין סופי או במקרה הסופי פשוט למספר עד n )
נקראת בת מנייה (מקור השם כי ניתן למנות/ למספר את האיברים בה ע"י התאמה חח"ע ועל מהטבעיים במקרה האין סופי או במקרה הסופי פשוט למספר עד n )
עוצמת הממשיים
תרגיל
הוכח כי עוצמת כל הקבוצות הבאות שווה - כל קטעים מהצורה ![[a,b],(a,b),[a,b),(a,b]](/images/math/f/a/2/fa230f7985742fb91303cd7422bb5db4.png) כאשר
כאשר 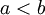 ואפשר כי
ואפשר כי 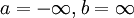
הוכחה:
קל לראות כי כל הקטעים הסופיים מהצורה ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . בעלי אותה עוצמה ע"י הפונקציה
. בעלי אותה עוצמה ע"י הפונקציה
באותו אופן כל הקטעים הסופיים מהצורה 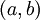 או
או ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) או
או 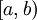 בעלי אותה עוצמה (כל הקטעים מאותו "סוג")
בעלי אותה עוצמה (כל הקטעים מאותו "סוג")
נמשיך- ט: הקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) בעל עוצמה שווה ל
בעל עוצמה שווה ל 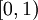 .
ה: נגדיר
.
ה: נגדיר ![f:[0,1)\rightarrow [0,1]](/images/math/e/d/a/eda56df2cb3f6442fbb661307d422b26.png) על ידי:
על ידי:
- אם
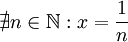 אזי נגדיר
אזי נגדיר 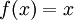
- אחרת נגדיר
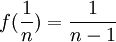
למעשה, כל מספר כמעט נשלח לעצמו פרט לסדרה הבת מנייה
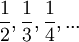
הנשלחת לסדרה
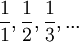 .
.
זה פונקציה חח"ע ועל.
הערה: אותה פונקציה מוכיחה כי הקטע ![(0,1]](/images/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) בעל עוצמה שווה ל
בעל עוצמה שווה ל 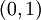 .
.
ט: הקטע ![(-1,0]](/images/math/2/9/1/291752b00d4774efa8912eafde589cc4.png) בעל עוצמה שווה ל
בעל עוצמה שווה ל 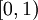 .
.
ה: ע"י הפונקציה 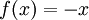
ט: הקטע 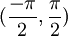 בעל עוצמה שווה ל
בעל עוצמה שווה ל  .
.
ה: הפונקציה 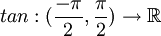 הפיכה בתחום הזה ולכן חח"ע ועל.
הפיכה בתחום הזה ולכן חח"ע ועל.
לסיום נעיר כי כל קרן (קטע עם צד אחד אין סופי) ג"כ בעלת אותה עוצמה כי היא מכילה איזה שהוא קטע ומוכלת בממשיים ולכן עפ"י קנטור ברנשטיין בעלת אותה עוצמה.
הגדרה: העוצמה של הממשיים מסומנת 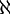 .
.
עוצמת הטבעיים קטנה ממש מעוצמת הממשיים
לשם הוכחת הטענה נשתמש בקבוצה המספרים 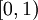 בכתיב עשרוני כלומר כל
בכתיב עשרוני כלומר כל 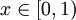 הוא מהצורה
הוא מהצורה 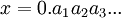 כאשר
כאשר 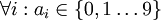 לשם נוחות התרגיל נזהה את x עם פונקציה
לשם נוחות התרגיל נזהה את x עם פונקציה 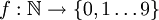 המוגדרת
המוגדרת 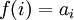
ט: 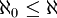
ה: נגדיר פונקציה 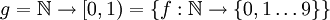
ע"י 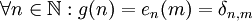 למשל 17 נשלח לפונקציה ששווה 0 בכל מקום פרט ל-17 ששם היא שווה 1
למשל 17 נשלח לפונקציה ששווה 0 בכל מקום פרט ל-17 ששם היא שווה 1
קל לראות כי g חח"ע.
כעת נניח בשלילה כי 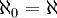 אזי יש פונקציה חח"ע ועל
אזי יש פונקציה חח"ע ועל
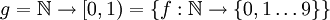 נסמן
נסמן 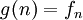 .
נראה כי g אינה על ע"י שנבנה פונקציה f שאין לה מקור:
.
נראה כי g אינה על ע"י שנבנה פונקציה f שאין לה מקור:
נגדיר 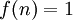 אם
אם 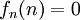 ו
ו 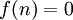 אחרת.
כעת לכל n
אחרת.
כעת לכל n 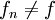 כי
כי 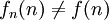 עפ"י הגדרת f. סתירה לכל ש g על.
עפ"י הגדרת f. סתירה לכל ש g על.
הערה: הזיהוי 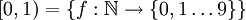 אינו מדויק כי
אינו מדויק כי 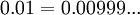 ולכן צריך להשלח לאותה פונקציה. נשאיר כתרגיל את דיוק ההוכחה.
ולכן צריך להשלח לאותה פונקציה. נשאיר כתרגיל את דיוק ההוכחה.
טענה. יהיו C,W קבוצות ויהיו 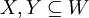 ,
, 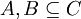 תתי קבוצות כך ש
תתי קבוצות כך ש 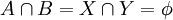 וגם
וגם 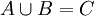 וגם
וגם 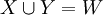 . אזי אם קיימות פונקציות חח"ע ועל
. אזי אם קיימות פונקציות חח"ע ועל 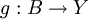 ,
,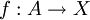 מתקיים ש
מתקיים ש 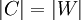
הוכחה:
לפי נתון קיימות 2 פונקציות חח"ע ועל 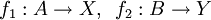
נגדיר 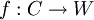 ע"י
ע"י 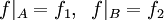 . בידקו שאכן f חח"ע ועל.
. בידקו שאכן f חח"ע ועל.
תרגיל ממבחן.
א. יהיו A,B קבוצות כך ש 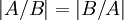 . הוכח ש
. הוכח ש 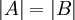 .
.
ב. מצא קבוצות A וB כך ש 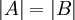 אבל
אבל 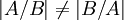 .
.
פתרון.
א. מתקיים 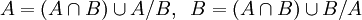 לפי נתון
לפי נתון 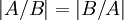 .
כיוון ש
.
כיוון ש 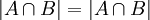 לפי תרגיל קודם סימנו.
לפי תרגיל קודם סימנו.
ב. ניקח את הטבעיים, ואת הטבעיים לאחר שזרקנו מהם את אחד. ברור שנשארנו עם קבוצות שוות עוצמה, אבל ההפרשים בינהם הם 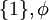 ואלו קבוצות מעוצמה שונה.
ואלו קבוצות מעוצמה שונה.
תרגילי העשרה (לא מומלץ להעביר בתירגול)
תרגיל.
נגדיר "שמיניה" בתור זוג עיגולים בגדלים כלשהם המשיקים זה לזה בנקודה כלשהי. יהי אוסף אינסופי כלשהו של שמיניות במישור הזרות זו מזו (כלומר אין שתים עם נקודת חיתוך משותפת)
א. הוכח שעוצמת קבוצה זו הינה אלף אפס
ב. הוכח שקיימת קבוצה של אינסוף עיגולים במרחב ללא חיתוך מעוצמת אלף
פתרון.
א. בהנתן שמיניה מסוימת באוסף, נבחר נקודה רציונאלית אחת מעיגול אחד, ואחת מהעיגול השני. זה נותן לנו פונקציה מהאוסף אל הזוגות הסדורים של מספרים רציונאליים.
כעת, נוכיח כי פונקציה זו הינה חח"ע. נניח בשלילה כי לשתי שמיניות שונות יש נקודות משותפים בשני העיגולים. אם כן, העיגול של האחת נמצא בעיגול של האחרת ולכן גם נקודת ההשקה נמצאת בתוך העיגול האחד. מכיוון שהעיגול השני מכיל נקודה משותפת עם העיגול השני של השמיניה השנייה, חייב להיות חיתוך בינהם בסתירה (ציור פה יקל ממש על ההבנה שלכם...).
לכן עוצמת האוסף קטנה מעוצמת הזוגות הסדורים של הרציונאליים, ולמדנו שזוגות סדורים של קבוצה בת מנייה היא קבוצה בת מנייה. לכן עוצמת האוסף קטנה מבת מנייה אבל מכיוון שהיא אינסופית היא גדולה מבת מנייה ולכן בת מנייה כדרוש.
ב. ניקח את אוסף העיגולים עם מרכז בראשית ורדיוס ממשי חיובי. אין בינהם חיתוך, והכמות שלהם זהה לחצי ציר הממשיים והוא כמובן מעוצמת אלף.