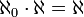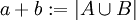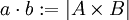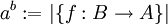הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 7"
(←אריתמטיקה של עוצמות) |
(←אריתמטיקה של עוצמות) |
||
| שורה 22: | שורה 22: | ||
'''הגדרה:''' | '''הגדרה:''' | ||
| − | יהיו שתי קבוצות A,B כך ש <math>|A|=a, |B|=b</math>. אזי נגדיר פעולות בין עוצמות: | + | יהיו שתי קבוצות '''זרות''' A,B כך ש <math>|A|=a, |B|=b</math>. אזי נגדיר פעולות בין עוצמות: |
*<math>a+b:=|A\cup B|</math> | *<math>a+b:=|A\cup B|</math> | ||
*<math>a\cdot b := |A\times B|</math> | *<math>a\cdot b := |A\times B|</math> | ||
גרסה מ־08:55, 7 באוקטובר 2011
אריתמטיקה של עוצמות
תרגיל. יהיו A,B קבוצות כך ש, עוצמת B גדולה מאחד. הוכח כי העוצמה של אוסף הפונקציות מA לB גדולה מעוצמת A.
פתרון.
קל לבנות פונקציה על מאוסף הפונקציות מA לB אל A. נשלח כל פונקציה באוסף למקור של איבר b מסוים. מכיוון שכל הפונקציות מA לB נמצאות באוסף, בפרט כל הפונקציות ששולחות כל איבר מA ל-b יהיו שם.
נניח בשלילה שקיימת התאמה חח"ע ועל בין A לבין אוסף הפונקציות הנ"ל. נסמן ב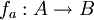 את הפונקציה המתאימה לאיבר
את הפונקציה המתאימה לאיבר 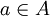 .
.
ידוע לנו שבקבוצה B יש לפחות שני איברים, לכן בהנתן אחד מהם אפשר לבחור את השני. נגדיר פונקציה באופן הבא 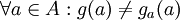 . לפי ההגדרות פונקציה זו הינה פונקציה מA לB אך אינה מתאימה לאף איבר בA בסתירה.
. לפי ההגדרות פונקציה זו הינה פונקציה מA לB אך אינה מתאימה לאף איבר בA בסתירה.
תרגיל. הוכח שעוצמת קבוצת החזקה של A תמיד גדולה מעוצמתה של A
הוכחה. קל להראות שקיימת העתקה חח"ע ועל בין אוסף הפונקציות 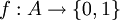 (כל קבוצה חלקית אומרת בעצם על כל איבר של A אם הוא שייך (1) או לא שייך (0). למשל הפונקציה המתאימה לקבוצה הריקה היא פונקצית האפס, והפונקציה המתאימה לקבוצה כולה היא הפונקציה 1).
(כל קבוצה חלקית אומרת בעצם על כל איבר של A אם הוא שייך (1) או לא שייך (0). למשל הפונקציה המתאימה לקבוצה הריקה היא פונקצית האפס, והפונקציה המתאימה לקבוצה כולה היא הפונקציה 1).
אוסף הפונקציות עומד בתנאי התרגיל לעיל ולכן עוצמתו גדולה מעוצמת A אבל זהה לעוצמה של קבוצת החזקה, כפי שרצינו.
הערה: מסיבה זו אוסף העוצמות אינו קבוצה אלא מחלקה. שכן אם הוא היה קבוצה, הייתה לו עוצמה
הגדרה:
יהיו שתי קבוצות זרות A,B כך ש 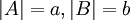 . אזי נגדיר פעולות בין עוצמות:
. אזי נגדיר פעולות בין עוצמות:
בהרצאה תוכיחו שהגדרות אלה מוגדרות היטב, כלומר העוצמה נשארת זהה ללא תלות בבחירת הקבוצות המייצגות.
שימו לב: מתוך הגדרה זו קל לראות את חוקי החזקות למקרי הקצה:
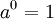 שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה.
שכן יש פונקציה יחידה מהקבוצה הריקה לכל מקום - היחס שהוא הקבוצה הריקה.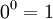 זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים
זה מקרה פרטי של הסעיף הקודם, ועדיין מתקיים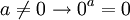 אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם.
אין אף פונקציה מקבוצה לא ריקה אל קבוצה ריקה, שכן יחס כזה לא יכול להיות שלם.
תכונות האריתמטיקה
בהנחת אקסיומת הבחירה:
- אם a או b מייצגים עוצמה אינסופית אזי
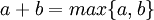
- אם a או b מייצגים עוצמה אינוספית ושניהם אינם אפס אזי
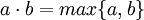
- אם
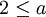 ו
ו 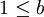 ולפחות אחת מבינהם הוא אינסופי אזי
ולפחות אחת מבינהם הוא אינסופי אזי 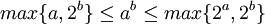
- מסקנה: אם
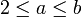 אזי
אזי 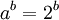
- מסקנה: אם
תרגיל ממבחן תשסח מועד א (ד"ר שי סרוסי וד"ר אלי בגנו)
תהי A קבוצה אינסופית. נסמן 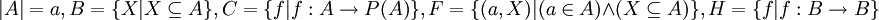
- א. מצא את
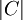
- ב. מצא את
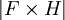
- ג. מצא את
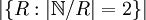 המוכלת באוסף יחסי השקילות על הטבעיים.
המוכלת באוסף יחסי השקילות על הטבעיים.
פתרון.
תרגיל ממבחן תשע מועד א (ד"ר שי סרוסי וד"ר אפי כהן)
יהי S יחס על 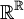 (קבוצת כל הפונקציות הממשיות), המוגדר על ידי
(קבוצת כל הפונקציות הממשיות), המוגדר על ידי 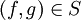 אם"ם לכל
אם"ם לכל 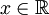 מתקיים
מתקיים 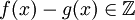
- 1. הוכיחו שS הינו יחס שקילות
- 2. תהי
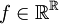 מצאו את
מצאו את ![|[f]|](/images/math/0/1/3/01364e045ffa77dc9f947de382b72c71.png)
- 3. מצאו את
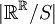
פתרון:
1.
- רפלקסיביות:
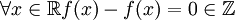
- סימטריות:
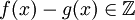 גורר שגם
גורר שגם 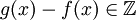 כי יש נגדי לחיבור
כי יש נגדי לחיבור - טרנזיטיביות: נובעת בקלות מסגירות לחיבור בשלמים:
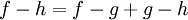
2.
נביט במחלקת השקילות של f ונראה שיש העתקה S חח"ע ועל ממנה לאוסף הפונקציות מהממשיים לשלמים.
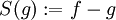 . לפי ההגדרה,
. לפי ההגדרה, 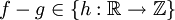 . נוכיח ש-S חח"ע ועל.
. נוכיח ש-S חח"ע ועל.
נניח 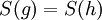 לכן
לכן  ולכן h=g, זה מוכיח חח"ע.
ולכן h=g, זה מוכיח חח"ע.
נוכיח על: תהי h פונקציה כלשהי מהממשיים לשלמים, ברור שf-h במחלקת השקילות של f.
אם כך, העוצמה של מחלקת השקילות זהה לעוצמה של אוסף הפונקציות מהממשיים לשלמים והוא 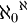 . לפי התכונות שלמדנו לעיל מתקיים
. לפי התכונות שלמדנו לעיל מתקיים 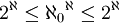 ולכן לפי קנטור מתקיים
ולכן לפי קנטור מתקיים 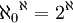
3.
נזכור בסימון 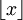 שהוא המספר השלם הגדול ביותר הקטן או שווה לx.
שהוא המספר השלם הגדול ביותר הקטן או שווה לx.
נגדיר S פונקציה השולחת את 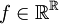 לפונקציה
לפונקציה 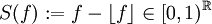 . נראה ש-S מוגדרת היטב בהתחשב ביחס השקילות שלנו, ובנוסף שהפונקציה השולחת מחלקת שקילות ל-S של נציג כלשהו של המחלקה הינה חח"ע ועל.
. נראה ש-S מוגדרת היטב בהתחשב ביחס השקילות שלנו, ובנוסף שהפונקציה השולחת מחלקת שקילות ל-S של נציג כלשהו של המחלקה הינה חח"ע ועל.
יהיו שתי פונקציות באותה מחלקת שקילות g,f. אזי, 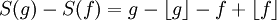 . מכיוון שזהו הפרש של שני מספרים אי שליליים קטנים מאחד, זה שווה למספר אי שלילי קטן מאחד. מכיוון שההפרש בין f ל-g שלם, המספר הזה הוא שלם. המספר השלם האי שלילי היחיד שקטן מאחד הינו אפס. לכן הפונקציה S מוגדרת היטב שכן היא שולחת נציגים שונים של מחלקת שקילות לאותו מקום.
. מכיוון שזהו הפרש של שני מספרים אי שליליים קטנים מאחד, זה שווה למספר אי שלילי קטן מאחד. מכיוון שההפרש בין f ל-g שלם, המספר הזה הוא שלם. המספר השלם האי שלילי היחיד שקטן מאחד הינו אפס. לכן הפונקציה S מוגדרת היטב שכן היא שולחת נציגים שונים של מחלקת שקילות לאותו מקום.
נניח בשלילה ש-S אינה חח"ע, לכן 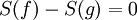 עבור נציגים ממחלקות שקילות שונות. אבל אז
עבור נציגים ממחלקות שקילות שונות. אבל אז 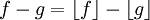 ולכן הם נציגים של אותה מחלקת שקילות בסתירה.
ולכן הם נציגים של אותה מחלקת שקילות בסתירה.
ניקח פונקציה כלשהי r מהממשיים לקטע 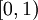 . קל לראות ש
. קל לראות ש ![S[r]=r](/images/math/3/4/d/34d5f08c63d392cbd4c350a0aec59420.png) שכן
שכן 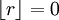 . לכן S הינה על.
. לכן S הינה על.
סה"כ קיבלנו שעוצמת קבוצת המנה שווה ל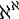 וזה שווה ל
וזה שווה ל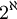 לפי התכונות לעיל.
לפי התכונות לעיל.
תרגיל ממבחן תשע מועד ב (ד"ר שי סרוסי וד"ר אפי כהן)
א. תהי A קבוצה אינסופית מעוצמה a.
- 1. נגדיר עבור
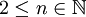 את הקבוצה הבאה:
את הקבוצה הבאה: ![Y=\{(X_1,...,X_n):n\in\mathbb{N}\and\Big[\bigcup_i X_i=A\Big] \and \Big[\forall i\neq j: X_i\cap X_j = \phi\Big]\}](/images/math/9/9/d/99dd40b5bbd79958762fc96879465b24.png) . הוכח
. הוכח 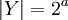
- 2. מצא את
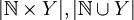 וגם את
וגם את 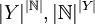
ב.תהי 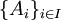 משפחה של קבוצות הזרות זו לזו. נסמן את עוצמת כל אחת מהן ב
משפחה של קבוצות הזרות זו לזו. נסמן את עוצמת כל אחת מהן ב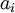 בהתאמה. נגדיר
בהתאמה. נגדיר 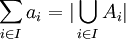 .
.
חשב את 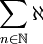
פתרון.
א.
- 1.
נביט באוסף הפונקציות 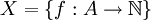 . נגדיר
. נגדיר 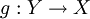 על ידי
על ידי 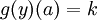 אם
אם 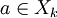 בתוך הn-יה הסדורה y. נוכיח שזו פונקציה מוגדרת היטב, חח"ע ועל.
בתוך הn-יה הסדורה y. נוכיח שזו פונקציה מוגדרת היטב, חח"ע ועל.
מוגדרת היטב: מכיוון שהקבוצות זרות ואיחודן שווה לA, האיבר a יופיע בדיוק באחת מהן.
חח"ע: נניח 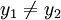 אזי יש איזה שתי תתי קבוצות של A שונות ביניהם, לכן יהיה איזה a באחת מהן שלא בשני שישלח למספר טבעי שונה.
אזי יש איזה שתי תתי קבוצות של A שונות ביניהם, לכן יהיה איזה a באחת מהן שלא בשני שישלח למספר טבעי שונה.
כעת, קל למצוא פונקציה חח"ע מקבוצת החזקה של A לY - נשלח כל תת קבוצה לזוג שמכיל אותה ואת המשלים שלה. את הקבוצה הריקה נשלח לשלישיה כלשהי.
העוצמה של אוסף הפונקציות לעיל הינה 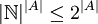 , וקבוצת החזקה הינה מעוצמה
, וקבוצת החזקה הינה מעוצמה 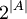 ולכן סה"כ עוצמת Y הינה
ולכן סה"כ עוצמת Y הינה 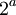 .
.
- 2.
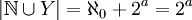
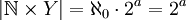
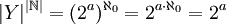
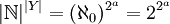
ב.
בעצם אנו רוצים לחשב איחוד בן מנייה של קבוצות מעוצמת 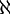 . לכל
. לכל 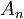 קיימת פונקציה חח"ע ועל
קיימת פונקציה חח"ע ועל 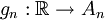 . לכן סה"כ נבנה פונקציה
. לכן סה"כ נבנה פונקציה 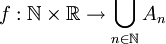 המוגדרת על ידי
המוגדרת על ידי 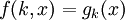 . מכיוון שהקבוצות זרות ו
. מכיוון שהקבוצות זרות ו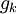 חח"ע ברור שf חח"ע. מכיוון ש
חח"ע ברור שf חח"ע. מכיוון ש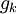 על גם f על ולכן סה"כ עוצמת הסכום הינה
על גם f על ולכן סה"כ עוצמת הסכום הינה