הבדלים בין גרסאות בדף "88-341 תשעג סמסטר א/תרגילים/תרגיל 2"
(←שאלה 4) |
מ (←שאלה 4) |
||
| שורה 25: | שורה 25: | ||
א. הוכיחו שאם <math>\left( E_n \right)_{n=1}^\infty</math> היא סדרת קבוצות יורדת (כלומר <math>E_1 \supseteq E_2 \supseteq E_3 \supseteq \dots</math>), ואם <math>\mu \left(E_1 \right)<\infty</math>, אזי | א. הוכיחו שאם <math>\left( E_n \right)_{n=1}^\infty</math> היא סדרת קבוצות יורדת (כלומר <math>E_1 \supseteq E_2 \supseteq E_3 \supseteq \dots</math>), ואם <math>\mu \left(E_1 \right)<\infty</math>, אזי | ||
| − | <math>\mu \left( \ | + | <math>\mu \left( \bigcap_{n=1}^\infty E_n \right)=\lim_{n \rightarrow \infty} \mu \left( E_n \right)</math> |
('''הדרכה:''' נסו לבנות סדרת קבוצות חדשה, כמו שעשיתם בהרצאה) | ('''הדרכה:''' נסו לבנות סדרת קבוצות חדשה, כמו שעשיתם בהרצאה) | ||
גרסה אחרונה מ־11:47, 11 בנובמבר 2012
שאלה 1
הוכיחו כי לכל קטע בעל מידה חיובית יש תת קבוצה לא מדידה. (הסתמכו על התרגיל הקודם).
שאלה 2
א. הוכיחו שקבוצת קנטור הטרנארית 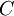 (זו מהתרגול) היא קומפקטית.
(זו מהתרגול) היא קומפקטית.
ב. הוכיחו שהפְּנים של קבוצת קנטור הוא ריק (קבוצות כאלה נקראות "קבוצות דלילות").
ג. הראו שקבוצת קנטור אינה איחוד בן-מנייה של קטעים סגורים (סעיף זה מראה שקבוצה סגורה ב-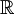 אינה בהכרח איחוד בן מנייה של קטעים סגורים - בניגוד למקרה של קבוצה פתוחה וקטעים פתוחים)
אינה בהכרח איחוד בן מנייה של קטעים סגורים - בניגוד למקרה של קבוצה פתוחה וקטעים פתוחים)
ד. הוכיחו כי 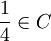 , למרות שרבע הוא אינו קצה של אף קטע בקבוצות
, למרות שרבע הוא אינו קצה של אף קטע בקבוצות 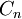 (רמז: נסו לפתח את רבע בבסיס 3).
(רמז: נסו לפתח את רבע בבסיס 3).
שאלה 3
תהי 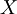 קבוצה כלשהי, ו-
קבוצה כלשהי, ו- 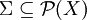 אוסף תתי הקבוצות של
אוסף תתי הקבוצות של 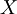 שהן בנות מנייה, או שהמשלים שלהן בן מנייה (כלומר
שהן בנות מנייה, או שהמשלים שלהן בן מנייה (כלומר 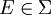 או"א
או"א  בת מנייה, או
בת מנייה, או 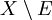 בת מנייה).
בת מנייה).
א. הוכיחו כי 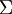 היא
היא 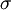 -אלגברה מעל
-אלגברה מעל 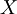 .
.
ב. נגדיר ![\mu : \Sigma \rightarrow [0,\infty]](/images/math/2/e/1/2e1ff153878c17cb6d37799ed65946d3.png) ע"י
ע"י 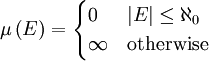 . הוכיחו כי זו מידה.
. הוכיחו כי זו מידה.
שאלה 4
יהי 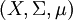 ממ"ח.
ממ"ח.
א. הוכיחו שאם 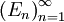 היא סדרת קבוצות יורדת (כלומר
היא סדרת קבוצות יורדת (כלומר 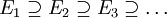 ), ואם
), ואם 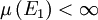 , אזי
, אזי
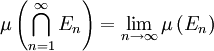
(הדרכה: נסו לבנות סדרת קבוצות חדשה, כמו שעשיתם בהרצאה)
ב. הראו שהדרישה 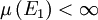 היא הכרחית (כלומר אם נוותר עליה, נוכל למצוא דוגמא נגדית).
היא הכרחית (כלומר אם נוותר עליה, נוכל למצוא דוגמא נגדית).
בהצלחה!