הבדלים בין גרסאות בדף "89-214 סמסטר א' תשעב/תקצירים"
(1-4) |
(הרצאות 5-8) |
||
| שורה 70: | שורה 70: | ||
לדוגמא, החבורה <math>\ \mathbb{Z}_n</math> ציקלית, משום שהיא נוצרת על-ידי המחלקה <math>\ [1]</math>. הסדר של a בחבורה הזו הוא <math>\ n/(a,n)</math>, ולכן יש בדיוק <math>\ \phi(n/e)</math> אברים מכל סדר n/e. בפרט, יש לחבורה <math>\ \mathbb{Z}_n</math> בדיוק <math>\ \phi(n)</math> יוצרים. | לדוגמא, החבורה <math>\ \mathbb{Z}_n</math> ציקלית, משום שהיא נוצרת על-ידי המחלקה <math>\ [1]</math>. הסדר של a בחבורה הזו הוא <math>\ n/(a,n)</math>, ולכן יש בדיוק <math>\ \phi(n/e)</math> אברים מכל סדר n/e. בפרט, יש לחבורה <math>\ \mathbb{Z}_n</math> בדיוק <math>\ \phi(n)</math> יוצרים. | ||
| + | |||
| + | == הרצאה חמישית == | ||
| + | |||
| + | כל תת-חבורה של <math>\ \mathbb{Z}_n</math> נוצרת על-ידי איבר המחלק את n; אם a|n, אז הסדר של החבורה הנוצרת על-ידי a הוא n/a, ולכן, אם H תת-חבורה של <math>\ \mathbb{Z}_n</math> מסדר d, היא שווה לחבורה הציקלית <n/d>. כלומר, לחבורות ציקליות יש תת-חבורה יחידה מכל סדר שמשפט לגרנז' מתיר. | ||
| + | |||
| + | מגדירים את המכפלה של תת-חבורות כקבוצה של כל המכפלות האפשריות: <math>\ AB=\{ab | a\in A, b\in B\}$</math>. באופן דומה אפשר להגדיר, לכל קבוצה בחבורה, <math>\ S^{-1}=\{s^{-1} | s\in S\}</math>. הוכחנו שאם A,B תת-חבורות, אז המכפלה AB תת-חבורה אם ורק אם AB=BA. | ||
| + | |||
| + | הגדרנו '''הומומורפיזם''' (העתקה מחבורה G לחבורה H, השומרת על הכפל (ולכן גם על איבר היחידה ועל פעולת ההיפוך)). התמונה של הומומורפיזם היא תת-חבורה של H, והגרעין הוא תת-חבורה של G. הומומורפיזם הוא חד-חד-ערכי אם ורק אם הגרעין שלו טריוויאלי. ראינו שכל תת-חבורה יכולה להיות תמונה של הומומורפיזם כלשהו. מאידך, לא כל תת-חבורה יכולה להיות גרעין של הומומורפיזם: לתת-חבורות כאלה נקרא בשעור הבא "תת-חבורות נורמליות", ובינתיים אנו מגדירים אותן על-פי התכונה <math>\ aH=Ha</math> לכל a, ותכונות השקולות לה. | ||
| + | |||
| + | תת-חבורה H של G המקיימת את התנאי <math>\ aHa^{-1} \subset H</math> לכל <math>\ a\in G</math>, (או כל אחד מהתנאים השקולים לכך) נקראת '''תת-חבורה נורמלית'''. | ||
| + | |||
| + | == הרצאה ששית == | ||
| + | |||
| + | אם <math>\ N\leq G</math> תת-חבורה נורמלית, מסמנים <math>\ N \triangleleft G</math>. הוכחנו שתת-חבורה היא נורמלית אם ורק אם המכפלה של קוסטים היא קוסט. את אוסף הקוסטים אפשר להפוך לחבורה, הקרויה '''חבורת המנה''', <math>\ G/N</math>. כמובן, <math>\ |G/N| = [G:N]</math>. קיומה של חבורת המנה מאפשר להוכיח קריטריון נוסף: תת-חבורה היא נורמלית אם ורק אם היא גרעין להומומורפיזם כלשהו (ההעתקה <math>\ \theta : G \rightarrow G/N</math> לפי <math>\ \theta(x) = xN</math> היא הומומורפיזם, ו- <math>\ \operatorname{Ker}(\theta) = N</math>). כלומר: תת-חבורות נורמליות של G = גרעינים של הומומורפיזמים מ-G. | ||
| + | |||
| + | הוכחנו את '''משפט האיזומורפיזם הראשון''': לכל הומומורפיזם <math>\ \phi : G \rightarrow H</math>, | ||
| + | <math>\ G/\operatorname{Ker}(\phi) \cong \operatorname{Im}(\phi)</math>. מעכשיו, אם נרצה להוכיח ש- <math>\ G/K \cong H</math>, מספיק יהיה לבנות אפימורפיזם (=הומומורפיזם על( <math>\ G \rightarrow H</math> שהגרעין שלו הוא K. | ||
| + | |||
| + | ראינו שנורמליות מחלחלת כלפי מטה: אם <math>\ K \triangleleft G</math> ו- <math>\ H \leq G</math>, אז <math>\ K \cap H \triangleleft H</math>. בפרט (אם מניחים <math>\ K \sub H</math>) נורמליות עוברת בתורשה לתת-חבורה. מאידך, נורמליות אינה טרנזיטיבית: יתכן ש- <math>N \triangleleft H \triangleleft G</math> ובכל זאת <math>\ N \not \triangleleft G</math>. | ||
| + | |||
| + | אם <math>\ N \triangleleft G</math> ו- <math>\ H \leq G</math> אז <math>\ NH</math> תמיד תת-חבורה; יתרה מזו, המכפלה של תת-חבורות נורמליות היא נורמלית. | ||
| + | |||
| + | הוכחנו, בעזרת משפט האיזומורפיזם הראשון, את משפט האיזומורפיזם השני (אם <math>\ N,H\leq G</math> ו-N נורמלית אז <math>\ H/(N\cap H)\cong HN/N</math>). | ||
| + | |||
| + | == הרצאה שביעית == | ||
| + | |||
| + | הוכחנו, שוב בעזרת משפט האיזומורפיזם הראשון, את משפט האיזומורפיזם השלישי (אם <math>\ K \leq N \leq G</math> ושתיהן נורמליות ב-G, אז <math>\ (G/K)/(N/K) \cong G/N</math>). | ||
| + | |||
| + | הסברנו את ההתאמה בין אוסף תת-החבורות של G המכילות תת-חבורה נורמלית K, לבין אוסף תת-החבורות של חבורת המנה G/K. ההתאמה הזו שומרת (בשני הכיוונים) על הכלה, ולכן היא חד-חד-ערכית ושומרת על חיתוך ומכפלה. היא שומרת גם על נורמליות ועל מנות ואינדקסים. '''תרגיל'''. נסח את הטענות האלה במפורש, והוכח אחת או שתיים מהן. | ||
| + | |||
| + | הגדרנו כמה מושגים הקשורים באברים מתחלפים: המרכז (מם צרויה) של חבורה G הוא אוסף האברים <math>\ Z(G)</math> המתחלפים עם כל אברי החבורה. זוהי תמיד תת-חבורה נורמלית. הראינו שהמרכז של החבורה הסימטרית הוא טריוויאלי. | ||
| + | |||
| + | המרכז (ריש פתוחה) של איבר g הוא אוסף האברים המתחלפים איתו, והמרכז (כנ"ל) של תת-חבורה הוא אוסף האברים המתחלפים עם כל איבר בחבורה. '''תרגיל''': כתוב, כפסוק על אברים בלבד, את שלוש הטענות הבאות: <math>\ A \subseteq C_G(B)</math>; <math>\ AB = BA</math>; <math>\ A \triangleleft AB</math>. | ||
| + | |||
| + | אברים x,g מתחלפים אם ורק אם הצמדת g על-ידי x אינה משנה את האיבר. ברוח זו, הגדרנו את יחס הצמידות על החבורה: שני אברים הם צמודים אם אפשר להגיע מאחד לשני על-ידי הצמדה, כלומר, הצמודים של x הם האברים מהצורה <math>\ g x g^{-1}</math>. הוכחנו שמספר האברים במחלקת הצמידות של a שווה לאינדקס <math>\ [G:C_G(a)]</math> של המרכז של האיבר בחבורה (ומכאן שמספר האברים הזה מחלק את סדר החבורה). | ||
| + | |||
| + | הפירוק של חבורה לאיחוד של מחלקות צמידות קובע את '''שוויון המחלקות''' <math>\ |G|=|Z(G)|+\sum [G:C_G(x)]</math>, שבו הסכום באגף ימין הוא על נציג אחד מכל מחלקה של אברים לא מרכזיים (המחלקה של איבר מרכזי כוללת אותו בלבד). | ||
| + | |||
| + | משוויון המחלקות מסיקים של"חבורת-p" (חבורה מסדר <math>\ p^n</math>) יש מרכז לא טריוויאלי. הראינו שאם G חבורה לא אבלית, אז המנה <math>\ G/Z(G)</math> אינה יכולה להיות ציקלית. בעזרת שתי התוצאות האחרונות אפשר למיין את כל החבורות מסדר <math>\ p^2</math> (כולן אבליות, ובהמשך נראה שיש רק שתיים כאלה - <math>\ \mathbb{Z}_{p^2}</math> ו- <math>\ \mathbb{Z}_p^2</math>), ואת כל החבורות הלא-אבליות מסדר <math>\ p^3</math> (יש שתיים). | ||
| + | |||
| + | == הרצאה שמינית == | ||
| + | |||
| + | אם H תת-חבורה נתונה, נסמן ב- <math>\ N_G(H) = \{g\in G: gHg^{-1} =H\}</math> את ה'''מנרמל''' של H. זוהי תת-החבורה הגדולה ביותר של G שבתוכה H נורמלית. הראינו שהאינדקס של המנרמל שווה למספר תת-החבורות של G הצמודות ל-H. | ||
| + | |||
| + | חבורת האוטומורפיזמים של חבורה G כוללת, לפי ההגדרה, את כל האוטומורפיזמים של החבורה (אלו הם הומומורפיזמים חד-חד-ערכיים ועל, מן החבורה אל עצמה). הצמדה באיבר של G מגדירה אוטומורפיזם, והפונקציה המתאימה לכל איבר את ההצמדה בו-עצמו היא הומומורפיזם, שהגרעין שלו הוא מרכז החבורה. התמונה נקראת "חבורת האוטומורפיזמים הפנימיים", והיא תת-חבורה נורמלית של חבורת האוטומורפיזמים. | ||
גרסה מ־17:29, 21 בדצמבר 2011
שימו לב: כשאתם נכנסים לתקצירי ההרצאות מהשנה שעברה, גם דף השיחה הוא מהשנה שעברה. את השאלות מתשע"ב כתבו בדף השיחה של הדף הזה.
תוכן עניינים
הרצאה ראשונה
מבוא לתורת המספרים
הנחת המוצא היא שאתם מכירים את התכונות היסודיות של המספרים השלמים (תכונות של החיבור והכפל, של הקבועים 0 ו-1, ושל יחס הסדר). תרגיל: איך אפשר להגדיר את הקבועים ואת יחס הסדר, אם נתונים רק החיבור והכפל? (פתרון: 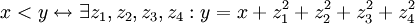 ).
).
הגדרנו את יחס החלוקה (שהוא יחס סדר חלש על אוסף הזוגות 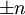 ), ואת המחלק המשותף המקסימלי (המחלק המשותף שהוא הגדול ביותר מכל המחלקים המשותפים, לפי היחס הרגיל), ואז הוכחנו שרשרת של טענות:
), ואת המחלק המשותף המקסימלי (המחלק המשותף שהוא הגדול ביותר מכל המחלקים המשותפים, לפי היחס הרגיל), ואז הוכחנו שרשרת של טענות:
1. אפשר לבצע חילוק עם שארית ("אוקלידיות");
2. המחלק המשותף המקסימלי של a ו- b הוא צירוף שלם שלהם.
3. אם 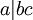 ו- a זר ל-b, אז
ו- a זר ל-b, אז 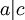 .
.
הגדרנו מספר אי-פריק (לא ניתן לפרק באופן לא-טריוויאלי) ומספר ראשוני (אם הוא מחלק מכפלה אז הוא מחלק את אחד הגורמים), והבחנו שכל ראשוני הוא אי-פריק (זה קל). כעת אפשר להוכיח
4. כל שלם אי-פריק הוא ראשוני (כלומר, במספרים השלמים, "ראשוני" ו"אי-פריק" הם בעצם אותו מושג), ואז
5. המשפט היסודי של האריתמטיקה: לכל מספר שלם יש פירוק יחיד לגורמים אי-פריקים.
השרשרת הזו תופיע באופן כללי בהרבה בפרק השלישי של הקורס, כאשר נעסוק בתחומי שלמות (שהם סוג מיוחד של חוגים קומוטטיביים (שהם סוג מיוחד של חוגים)).
תרגיל. בכתה הגדרנו מחלק משותף מקסימלי לגבי יחס הסדר הרגיל, ואמרנו שלו היינו מגדירים לפי יחס החלוקה היינו מקבלים אותו הדבר. הוכיחו טענה זו. כלומר, הראו שכל מחלק משותף של a ו-b מחלק את המחלק המשותף המקסימלי.
הרצאה שניה
לסיום הפרק הראשון הגדרנו את יחס השקילות 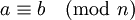 (אם ורק אם
(אם ורק אם 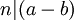 ). מחלקות השקילות שלו הן
). מחלקות השקילות שלו הן ![\ \mathbb{Z}_n = \{[0],[1],\dots,[n-1]\}](/images/math/f/8/c/f8c7dd20a5ac8955cccb218b3b410214.png) . מתברר שפעולות החיבור והכפל לפי רכיבים מגדירות פעולות בין המחלקות. משפט השאריות הסיני קובע שאם n,m זרים, אז הפונקציה
. מתברר שפעולות החיבור והכפל לפי רכיבים מגדירות פעולות בין המחלקות. משפט השאריות הסיני קובע שאם n,m זרים, אז הפונקציה 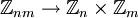 המוגדרת על-ידי
המוגדרת על-ידי ![\ [x]_{nm} \mapsto ([x]_n,[x]_m)](/images/math/b/7/3/b73ec4b01d12da938f1dfcc0e0b3b3d3.png) (תרגיל: הוכח שהיא מוגדרת היטב; מה יש לבדוק?) היא חד-חד-ערכית ועל.
(תרגיל: הוכח שהיא מוגדרת היטב; מה יש לבדוק?) היא חד-חד-ערכית ועל.
מערכת מתמטית כוללת קבוצה, פעולות, יחסים וקבועים (או חלק מהם). המשך הקורס יעסוק בכמה מערכות מתמטיות חשובות: חבורות, חוגים ושדות. לפני שנעסוק בחבורות באופן ישיר, נפגוש שני מבנים אלגבריים פשוטים יותר: חבורות למחצה ומונוידים.
חבורה למחצה היא קבוצה עם פעולה בינארית אסוציאטיבית. דוגמא כללית: אוסף כל הפונקציות מקבוצה X לעצמה. (במובן מסויים, כל חבורה למחצה היא אוסף של פונקציות מקבוצה מתאימה לעצמה [בעתיד נוכיח תוצאה דומה על חבורות]). שימו לב שכדי שקבוצה חלקית של אוסף כל הפונקציות מ-X ל-X תהיה חבורה למחצה, די בכך שהיא תהיה סגורה להרכבה (משום שהאסוציאטיביות היא אוטומטית).
איבר של חבורה למחצה המקיים את התנאי 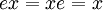 לכל x הוא "איבר יחידה". לא תמיד יש כזה, אבל אם הוא קיים - הוא יחיד. חבורה למחצה שבה יש איבר יחידה, נקראת מונויד (או "יחידון").
לכל x הוא "איבר יחידה". לא תמיד יש כזה, אבל אם הוא קיים - הוא יחיד. חבורה למחצה שבה יש איבר יחידה, נקראת מונויד (או "יחידון").
הרצאה שלישית
איבר y של מונויד M הוא "הפכי של x" אם xy=yx=1. אם יש ל-x הפכי, אז הוא יחיד --- ולאיבר הזה קוראים "ההפכי של x". איבר שיש לו הפכי הוא "איבר הפיך". לדוגמא, איבר היחידה הוא הפיך --- אבל יש מונוידים שבהם אין אף איבר
הפיך אחר. מונויד שכל האיברים שלו הפיכים נקרא חבורה. מתברר שבכל מונויד M, אוסף האיברים ההפיכים 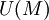 הוא חבורה.
הוא חבורה.
המונויד מקיים את תכונת הצמצום משמאל אם מ-xy=xz תמיד נובע y=z. לדוגמא, המונויד של המספרים עד n עם פעולת המקסימום אינו מקיים את התכונה הזו. מונויד המוכל בחבורה מקיים את תכונת הצמצום (אבל יש דוגמאות - קשות יחסית - למונוידים המקיימים את תכונת הצמצום ואינם מוכלים באף חבורה).
משפט. מונויד סופי בעל תכונת הצמצום משמאל הוא חבורה.
דוגמאות לחבורות.
-
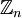 ביחס לפעולת החיבור.
ביחס לפעולת החיבור. - אוסף האברים ההפיכים ב-
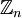 ביחס לפעולת הכפל. לחבורה הזו קוראים חבורת אוילר מסדר n, ויש בה
ביחס לפעולת הכפל. לחבורה הזו קוראים חבורת אוילר מסדר n, ויש בה 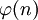 אברים.
אברים. - החבורה הסימטרית
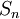 היא חבורת התמורות על n עצמים. אפשר לכתוב כל תמורה כמכפלה של מחזורים זרים, באופן יחיד.
היא חבורת התמורות על n עצמים. אפשר לכתוב כל תמורה כמכפלה של מחזורים זרים, באופן יחיד. - לכל שדה F, המטריצות ההפיכות מסדר n מעל F מהוות חבורה,
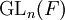 .
.
אפשר להגדיר מכפלה ישרה חיצונית, שהיא המכפלה הקרטזית של שתי חבורות נתונות עם הפעולה לפי רכיבים, כדרך לבנות חבורה חדשה מחבורות נתונות.
הרצאה רביעית
תת-קבוצה לא-ריקה H של חבורה G היא תת-חבורה אם H מהווה חבורה בזכות עצמה ביחס לפעולות המצומצמות מ-G. זה שקול לכך שהיא סגורה לכפל וללקיחת הפכי (בחבורה סופית, די בכך שהקבוצה סגורה לכפל). תת-החבורות הטריוויאליות הן G עצמה, והקבוצה הכוללת רק את איבר היחידה.
אם H תת-חבורה של G, קבוצה מהצורה 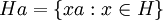 נקראת קוסט שמאלי של H. הקוסטים השמאליים זרים זה לזה, והם מכסים את החבורה. מכיוון שלכולם אותו גודל (השווה לסדר של H), מתקבל משפט לגרנז': הסדר של חבורה (סופית) מתחלק בסדר של כל תת-חבורה.
נקראת קוסט שמאלי של H. הקוסטים השמאליים זרים זה לזה, והם מכסים את החבורה. מכיוון שלכולם אותו גודל (השווה לסדר של H), מתקבל משפט לגרנז': הסדר של חבורה (סופית) מתחלק בסדר של כל תת-חבורה.
מסקנות מעניינות: משפט פרמה ומשפט אוילר.
תרגיל. הוכיחו שלתת-חבורה נתונה H, יש אותו מספר קוסטים ימניים ושמאליים (משפט לגרנז' פותר בקלות את המקרה שבו G סופית, אבל הטענה נכונה באופן כללי; כן, גם לתת-חבורה אינסופית של חבורה אינסופית יכולים להיות מספר סופי של קוסטים - תנו דוגמא לתופעה כזו).
חיתוך של אוסף כלשהו של תת-חבורות הוא תת-חבורה, וכך אפשר להגדיר את החבורה הנוצרת על-ידי קבוצה S, כתת-החבורה הקטנה ביותר המכילה את S. אבריה של תת-החבורה הזו הם המכפלות של אברי S וההפכיים שלהם.
הסדר של איבר 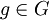 הוא n>0 הקטן ביותר שעבורו
הוא n>0 הקטן ביותר שעבורו 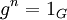 (אם יש כזה; אחרת הסדר הוא אינסוף). כל איבר g יוצר תת-חבורה
(אם יש כזה; אחרת הסדר הוא אינסוף). כל איבר g יוצר תת-חבורה 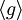 , הכוללת בדיוק את החזקות של g; סדר החבורה הזו שווה לסדר האיבר. חבורות כאלה, הנוצרות על-ידי איבר אחד, נקראות חבורות ציקליות.
, הכוללת בדיוק את החזקות של g; סדר החבורה הזו שווה לסדר האיבר. חבורות כאלה, הנוצרות על-ידי איבר אחד, נקראות חבורות ציקליות.
לדוגמא, החבורה 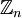 ציקלית, משום שהיא נוצרת על-ידי המחלקה
ציקלית, משום שהיא נוצרת על-ידי המחלקה ![\ [1]](/images/math/4/b/7/4b79bb225f2c74c899a26fa95f807ab5.png) . הסדר של a בחבורה הזו הוא
. הסדר של a בחבורה הזו הוא 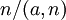 , ולכן יש בדיוק
, ולכן יש בדיוק 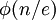 אברים מכל סדר n/e. בפרט, יש לחבורה
אברים מכל סדר n/e. בפרט, יש לחבורה 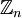 בדיוק
בדיוק 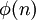 יוצרים.
יוצרים.
הרצאה חמישית
כל תת-חבורה של 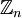 נוצרת על-ידי איבר המחלק את n; אם a|n, אז הסדר של החבורה הנוצרת על-ידי a הוא n/a, ולכן, אם H תת-חבורה של
נוצרת על-ידי איבר המחלק את n; אם a|n, אז הסדר של החבורה הנוצרת על-ידי a הוא n/a, ולכן, אם H תת-חבורה של 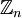 מסדר d, היא שווה לחבורה הציקלית <n/d>. כלומר, לחבורות ציקליות יש תת-חבורה יחידה מכל סדר שמשפט לגרנז' מתיר.
מסדר d, היא שווה לחבורה הציקלית <n/d>. כלומר, לחבורות ציקליות יש תת-חבורה יחידה מכל סדר שמשפט לגרנז' מתיר.
מגדירים את המכפלה של תת-חבורות כקבוצה של כל המכפלות האפשריות: 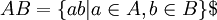 . באופן דומה אפשר להגדיר, לכל קבוצה בחבורה,
. באופן דומה אפשר להגדיר, לכל קבוצה בחבורה, 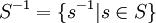 . הוכחנו שאם A,B תת-חבורות, אז המכפלה AB תת-חבורה אם ורק אם AB=BA.
. הוכחנו שאם A,B תת-חבורות, אז המכפלה AB תת-חבורה אם ורק אם AB=BA.
הגדרנו הומומורפיזם (העתקה מחבורה G לחבורה H, השומרת על הכפל (ולכן גם על איבר היחידה ועל פעולת ההיפוך)). התמונה של הומומורפיזם היא תת-חבורה של H, והגרעין הוא תת-חבורה של G. הומומורפיזם הוא חד-חד-ערכי אם ורק אם הגרעין שלו טריוויאלי. ראינו שכל תת-חבורה יכולה להיות תמונה של הומומורפיזם כלשהו. מאידך, לא כל תת-חבורה יכולה להיות גרעין של הומומורפיזם: לתת-חבורות כאלה נקרא בשעור הבא "תת-חבורות נורמליות", ובינתיים אנו מגדירים אותן על-פי התכונה 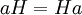 לכל a, ותכונות השקולות לה.
לכל a, ותכונות השקולות לה.
תת-חבורה H של G המקיימת את התנאי 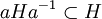 לכל
לכל 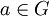 , (או כל אחד מהתנאים השקולים לכך) נקראת תת-חבורה נורמלית.
, (או כל אחד מהתנאים השקולים לכך) נקראת תת-חבורה נורמלית.
הרצאה ששית
אם 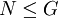 תת-חבורה נורמלית, מסמנים
תת-חבורה נורמלית, מסמנים 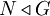 . הוכחנו שתת-חבורה היא נורמלית אם ורק אם המכפלה של קוסטים היא קוסט. את אוסף הקוסטים אפשר להפוך לחבורה, הקרויה חבורת המנה,
. הוכחנו שתת-חבורה היא נורמלית אם ורק אם המכפלה של קוסטים היא קוסט. את אוסף הקוסטים אפשר להפוך לחבורה, הקרויה חבורת המנה, 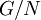 . כמובן,
. כמובן, ![\ |G/N| = [G:N]](/images/math/e/e/b/eeb31922a71f8e8359c9b8c07c5283b5.png) . קיומה של חבורת המנה מאפשר להוכיח קריטריון נוסף: תת-חבורה היא נורמלית אם ורק אם היא גרעין להומומורפיזם כלשהו (ההעתקה
. קיומה של חבורת המנה מאפשר להוכיח קריטריון נוסף: תת-חבורה היא נורמלית אם ורק אם היא גרעין להומומורפיזם כלשהו (ההעתקה  לפי
לפי 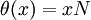 היא הומומורפיזם, ו-
היא הומומורפיזם, ו- 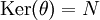 ). כלומר: תת-חבורות נורמליות של G = גרעינים של הומומורפיזמים מ-G.
). כלומר: תת-חבורות נורמליות של G = גרעינים של הומומורפיזמים מ-G.
הוכחנו את משפט האיזומורפיזם הראשון: לכל הומומורפיזם 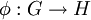 ,
,
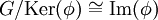 . מעכשיו, אם נרצה להוכיח ש-
. מעכשיו, אם נרצה להוכיח ש- 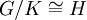 , מספיק יהיה לבנות אפימורפיזם (=הומומורפיזם על(
, מספיק יהיה לבנות אפימורפיזם (=הומומורפיזם על( 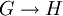 שהגרעין שלו הוא K.
שהגרעין שלו הוא K.
ראינו שנורמליות מחלחלת כלפי מטה: אם 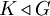 ו-
ו- 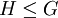 , אז
, אז 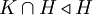 . בפרט (אם מניחים
. בפרט (אם מניחים 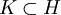 ) נורמליות עוברת בתורשה לתת-חבורה. מאידך, נורמליות אינה טרנזיטיבית: יתכן ש-
) נורמליות עוברת בתורשה לתת-חבורה. מאידך, נורמליות אינה טרנזיטיבית: יתכן ש- 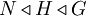 ובכל זאת
ובכל זאת 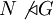 .
.
אם 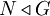 ו-
ו- 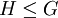 אז
אז 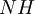 תמיד תת-חבורה; יתרה מזו, המכפלה של תת-חבורות נורמליות היא נורמלית.
תמיד תת-חבורה; יתרה מזו, המכפלה של תת-חבורות נורמליות היא נורמלית.
הוכחנו, בעזרת משפט האיזומורפיזם הראשון, את משפט האיזומורפיזם השני (אם 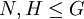 ו-N נורמלית אז
ו-N נורמלית אז 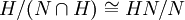 ).
).
הרצאה שביעית
הוכחנו, שוב בעזרת משפט האיזומורפיזם הראשון, את משפט האיזומורפיזם השלישי (אם 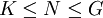 ושתיהן נורמליות ב-G, אז
ושתיהן נורמליות ב-G, אז 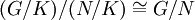 ).
).
הסברנו את ההתאמה בין אוסף תת-החבורות של G המכילות תת-חבורה נורמלית K, לבין אוסף תת-החבורות של חבורת המנה G/K. ההתאמה הזו שומרת (בשני הכיוונים) על הכלה, ולכן היא חד-חד-ערכית ושומרת על חיתוך ומכפלה. היא שומרת גם על נורמליות ועל מנות ואינדקסים. תרגיל. נסח את הטענות האלה במפורש, והוכח אחת או שתיים מהן.
הגדרנו כמה מושגים הקשורים באברים מתחלפים: המרכז (מם צרויה) של חבורה G הוא אוסף האברים 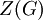 המתחלפים עם כל אברי החבורה. זוהי תמיד תת-חבורה נורמלית. הראינו שהמרכז של החבורה הסימטרית הוא טריוויאלי.
המתחלפים עם כל אברי החבורה. זוהי תמיד תת-חבורה נורמלית. הראינו שהמרכז של החבורה הסימטרית הוא טריוויאלי.
המרכז (ריש פתוחה) של איבר g הוא אוסף האברים המתחלפים איתו, והמרכז (כנ"ל) של תת-חבורה הוא אוסף האברים המתחלפים עם כל איבר בחבורה. תרגיל: כתוב, כפסוק על אברים בלבד, את שלוש הטענות הבאות: 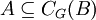 ;
; 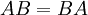 ;
; 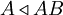 .
.
אברים x,g מתחלפים אם ורק אם הצמדת g על-ידי x אינה משנה את האיבר. ברוח זו, הגדרנו את יחס הצמידות על החבורה: שני אברים הם צמודים אם אפשר להגיע מאחד לשני על-ידי הצמדה, כלומר, הצמודים של x הם האברים מהצורה 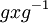 . הוכחנו שמספר האברים במחלקת הצמידות של a שווה לאינדקס
. הוכחנו שמספר האברים במחלקת הצמידות של a שווה לאינדקס ![\ [G:C_G(a)]](/images/math/5/c/8/5c8880d0f658f63454c43f86ff077c1e.png) של המרכז של האיבר בחבורה (ומכאן שמספר האברים הזה מחלק את סדר החבורה).
של המרכז של האיבר בחבורה (ומכאן שמספר האברים הזה מחלק את סדר החבורה).
הפירוק של חבורה לאיחוד של מחלקות צמידות קובע את שוויון המחלקות ![\ |G|=|Z(G)|+\sum [G:C_G(x)]](/images/math/5/a/0/5a014e2a34655e70dedbde335c95de5d.png) , שבו הסכום באגף ימין הוא על נציג אחד מכל מחלקה של אברים לא מרכזיים (המחלקה של איבר מרכזי כוללת אותו בלבד).
, שבו הסכום באגף ימין הוא על נציג אחד מכל מחלקה של אברים לא מרכזיים (המחלקה של איבר מרכזי כוללת אותו בלבד).
משוויון המחלקות מסיקים של"חבורת-p" (חבורה מסדר 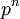 ) יש מרכז לא טריוויאלי. הראינו שאם G חבורה לא אבלית, אז המנה
) יש מרכז לא טריוויאלי. הראינו שאם G חבורה לא אבלית, אז המנה 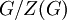 אינה יכולה להיות ציקלית. בעזרת שתי התוצאות האחרונות אפשר למיין את כל החבורות מסדר
אינה יכולה להיות ציקלית. בעזרת שתי התוצאות האחרונות אפשר למיין את כל החבורות מסדר 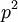 (כולן אבליות, ובהמשך נראה שיש רק שתיים כאלה -
(כולן אבליות, ובהמשך נראה שיש רק שתיים כאלה - 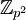 ו-
ו- 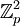 ), ואת כל החבורות הלא-אבליות מסדר
), ואת כל החבורות הלא-אבליות מסדר 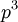 (יש שתיים).
(יש שתיים).
הרצאה שמינית
אם H תת-חבורה נתונה, נסמן ב- 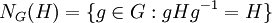 את המנרמל של H. זוהי תת-החבורה הגדולה ביותר של G שבתוכה H נורמלית. הראינו שהאינדקס של המנרמל שווה למספר תת-החבורות של G הצמודות ל-H.
את המנרמל של H. זוהי תת-החבורה הגדולה ביותר של G שבתוכה H נורמלית. הראינו שהאינדקס של המנרמל שווה למספר תת-החבורות של G הצמודות ל-H.
חבורת האוטומורפיזמים של חבורה G כוללת, לפי ההגדרה, את כל האוטומורפיזמים של החבורה (אלו הם הומומורפיזמים חד-חד-ערכיים ועל, מן החבורה אל עצמה). הצמדה באיבר של G מגדירה אוטומורפיזם, והפונקציה המתאימה לכל איבר את ההצמדה בו-עצמו היא הומומורפיזם, שהגרעין שלו הוא מרכז החבורה. התמונה נקראת "חבורת האוטומורפיזמים הפנימיים", והיא תת-חבורה נורמלית של חבורת האוטומורפיזמים.