האינטגרל לפי דרבו (המשך)[עריכה]

משפט 8[עריכה]

נניח ש-f מוגדרת וחסומה בקטע [math]\displaystyle{ [a,c] }[/math] ונניח ש-[math]\displaystyle{ a\lt b\lt c }[/math]. אזי f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וב-[math]\displaystyle{ [b,c] }[/math] אם"ם היא אינטגרבילית ב-[math]\displaystyle{ [a,c] }[/math], ואם כן מתקיים [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math].

הוכחה[עריכה]

[math]\displaystyle{ \implies }[/math]: נתונה f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וב-[math]\displaystyle{ [b,c] }[/math]. נקח חלוקה כלשהי P של [math]\displaystyle{ [a,b] }[/math] וחלוקה Q של [math]\displaystyle{ [b,c] }[/math] ונגדיר [math]\displaystyle{ R=P\cup Q }[/math] (כלומר R חלוקה של [math]\displaystyle{ [a,c] }[/math]). לכן מתקיים [math]\displaystyle{ \overline S(f,R)=\overline S(f,P)+\overline S(f,Q) }[/math]. נשאיף [math]\displaystyle{ \lambda(P),\lambda(Q)\to0 }[/math]. לפי הנתון [math]\displaystyle{ \overline S(f,P)\to\int\limits_a^b f }[/math] וגם [math]\displaystyle{ \overline S(f,Q)\to\int\limits_b^c f }[/math], לכן [math]\displaystyle{ \overline S(f,R)\to\int\limits_a^b f+\int\limits_b^c f }[/math]. באותו אופן נקבל [math]\displaystyle{ \underline S(f,R)\to\int\limits_a^b f+\int\limits_b^c f }[/math]. הראנו ש-[math]\displaystyle{ \overline S(f,R)-\underline S(f,R)\to0 }[/math] ולכן f אינטגרבילית ב-[math]\displaystyle{ [a,c] }[/math]. ע"פ משפט 4 נסיק [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math].

[math]\displaystyle{ \Longleftarrow }[/math]: נבחר חלוקות P,Q,R כמו בחלק הקודם, ושוב [math]\displaystyle{ \overline S(f,R)=\overline S(f,P)+\overline S(f,Q) }[/math] ו-[math]\displaystyle{ \underline S(f,R)=\underline S(f,P)+\underline S(f,Q) }[/math]. נחסיר ונקבל: [math]\displaystyle{ \overline S(f,R)-\underline S(f,R)=\overline S(f,P)-\underline S(f,P)+\overline S(f,Q)-\underline S(f,Q) }[/math]. כעת, אם [math]\displaystyle{ \varepsilon\gt 0 }[/math], האינטגרביליות של f על [math]\displaystyle{ [a,c] }[/math] גוררת שעבור [math]\displaystyle{ \lambda(P) }[/math] ו-[math]\displaystyle{ \lambda(Q) }[/math] מספיק קטנים [math]\displaystyle{ \overline S(f,P)-\underline S(f,P),\overline S(f,Q)-\underline S(f,Q)\lt \varepsilon }[/math]. קיום חלוקה P כזאת לכל [math]\displaystyle{ \varepsilon\gt 0 }[/math] מוכיח ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וקיום חלוקה Q - ב-[math]\displaystyle{ [b,c] }[/math]. השיוויון [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math] נובע מהחלק הקודם. [math]\displaystyle{ \blacksquare }[/math]

הכללה[עריכה]

אם [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math] ואם f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] אז [math]\displaystyle{ \int\limits_a^b f=\sum_{k=1}^n\int\limits_{x_{k-1}}^{x_k} f }[/math]. ההוכחה באינדוקציה.

מוסכמות:

[math]\displaystyle{ \int\limits_a^a f=0 }[/math]
אם [math]\displaystyle{ a\lt b }[/math] ואם f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] נרשום [math]\displaystyle{ \int\limits_b^a f=-\int\limits_a^b f }[/math]

(אלה מוסכמות ולא משפטים כי באופן שבו הגדרנו את האינטגרל עד עכשיו, [math]\displaystyle{ \int\limits_b^a }[/math] לא מוגדר עבור [math]\displaystyle{ a\le b }[/math])

עם מוסכמות אלה יתקיים:

[math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math] באופן בלתי תלוי בסדר של המספרים a,b,c. למשל, אם [math]\displaystyle{ c\lt a\lt b }[/math] אז לפי משפט 8 [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math]. נבדוק: [math]\displaystyle{ \int\limits_c^a f=-\int\limits_a^c f\ \and\ \int\limits_c^b f=-\int\limits_b^c f }[/math] ולכן [math]\displaystyle{ -\int\limits_b^c f=-\int\limits_a^c f+\int\limits_a^b f }[/math], מה שגורר [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math].

משפט 9[עריכה]

תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. עוד נניח ש-f רציפה ב-[math]\displaystyle{ (a,b] }[/math]. אזי f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math].

הוכחה[עריכה]

יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. נגדיר [math]\displaystyle{ c=a+\frac\varepsilon{2\Omega} }[/math]. לפי הנתון f רציפה ב-[math]\displaystyle{ [c,b] }[/math], אזי ממשפט 6 היא אינטגרבילית ב-[math]\displaystyle{ [c,b] }[/math], לכן נוכל לבחור חלוקה P של [math]\displaystyle{ [c,b] }[/math] כך ש-[math]\displaystyle{ \overline S(f,P)-\underline S(f,P)\lt \frac\varepsilon2 }[/math]. כעת נגדיר חלוקה Q של [math]\displaystyle{ [a,b] }[/math] ע"י [math]\displaystyle{ Q=\{a\}\cup P }[/math]. עוד נגדיר [math]\displaystyle{ M'=\sup\{f(x):\ a\le x\le c\} }[/math] וכן [math]\displaystyle{ m'=\inf\{f(x):\ a\le x\le c\} }[/math]. נובע כי

[math]\displaystyle{ \begin{align}\overline S(f,Q)-\underline S(f,Q)&=(M'-m')(c-a)+\overline S(f,P)-\underline S(f,P)\\&\lt \Omega(c-a)+\frac\varepsilon2\\&=\Omega\cdot\frac\varepsilon{2\Omega}+\frac\varepsilon2\\&=\varepsilon\end{align} }[/math]

נובע ממשפט 4 ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math]. [math]\displaystyle{ \blacksquare }[/math]

מסקנה 1[עריכה]

המשפט נכון אם f חסומה ורציפה ב-[math]\displaystyle{ (a,b) }[/math].

מסקנה 2[עריכה]

נניח ש-f חסומה ב-[math]\displaystyle{ [a,b] }[/math] ורציפה שם פרט למספר סופי של נקודות [math]\displaystyle{ x_0,x_1,\dots,x_n }[/math] כך ש-[math]\displaystyle{ a\le x_0\lt x_1\lt \dots\lt x_n\le b }[/math]. אזי f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math].

הוכחה[עריכה]

עבור כל k נקבל ש-f חסומה ב-[math]\displaystyle{ [x_{k-1},x_k] }[/math] ורציפה ב-[math]\displaystyle{ (x_{k-1},x_k) }[/math]. לפי מסקנה 1, f אינטגרבילית ב-[math]\displaystyle{ [x_{k-1},x_k] }[/math]. נסתמך על ההכללה למשפט 8 לומר ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b]=\bigcup_{k=1}^n [x_{k-1},x_k] }[/math]. [math]\displaystyle{ \blacksquare }[/math]

דוגמה לפונקציה רציפה למקוטעין

הגדרה: אומרים ש-f "רציפה למקוטעין" ב-[math]\displaystyle{ [a,b] }[/math] אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון.

נובע ממסקנה 2 שכל פונקציה רציפה למקוטעין ב-[math]\displaystyle{ [a,b] }[/math] אינטגרבילית שם. באופן דומה אפשר להוכיח שאם f מוגדרת ו"מונוטונית למקוטעין" ב-[math]\displaystyle{ [a,b] }[/math] אז היא אינטגרבילית שם.

האינטגרל לפי רימן[עריכה]

הקדמה - הגישה של רימן[עריכה]

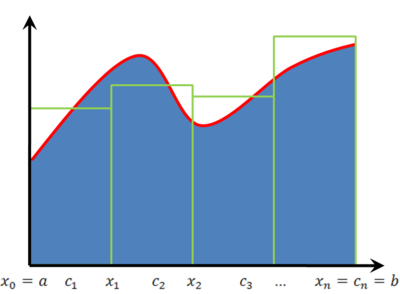
ניתן לראות שסכום שטחי המלבנים הנוצרים מסכום רימן שווה בקירוב לשטח שמתחת לגרף.

נניח ש-f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. נבחר חלוקה P של [math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math]. עוד נבחר לכל k מספר [math]\displaystyle{ c_k\in[x_{k-1},x_k] }[/math] ונכנה כ-P' את התת חלוקה [math]\displaystyle{ a\le c_1\lt c_2\lt \dots\lt c_n\le b }[/math]. ז"א [math]\displaystyle{ a=x_0\le c_1\le x_1\le c_2\le\dots\le c_n\le x_n=b }[/math]. בהתאם לכך נבנה סכום רימן [math]\displaystyle{ S(f,P,P')=\sum_{k=1}^n f(c_k)\Delta x_k }[/math] כאשר לכל k מתקיים [math]\displaystyle{ \Delta x_k=x_k-x_{k-1} }[/math].

[math]\displaystyle{ S(f,P,P') }[/math] מקרב את השטח שמתחת לגרף, אך לא ידוע אם הוא גדול, קטן או שווה לו.

נעיר שעל חלוקה אחת P של [math]\displaystyle{ [a,b] }[/math] אפשר לבנות אינסוף סכומי רימן [math]\displaystyle{ S(f,P,P') }[/math]. עם זאת, יתקיים תמיד [math]\displaystyle{ \underline S(f,P)\le S(f,P,P')\le\overline S(f,P) }[/math]. יתר על כן, [math]\displaystyle{ \underline S(f,P)=\inf_{P'} S(f,P,P') }[/math] ו-[math]\displaystyle{ \overline S(f,P)=\sup_{P'} S(f,P,P') }[/math].

הגדרת האינטגרל לפי רימן: תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. נאמר ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] אם כאשר [math]\displaystyle{ \lambda(P)\to0 }[/math] כל סכומי רימן [math]\displaystyle{ S(f,P,P') }[/math] שואפים לגבול אחד, שיסומן [math]\displaystyle{ \int\limits_a^b f }[/math].

משפט 10[עריכה]

תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. אזי f אינטגרבילית שם לפי רימן אם"ם f אינטגרבילית שם לפי דרבו, ואם כן אז [math]\displaystyle{ {\int\limits_R}_a^b f }[/math] (לפי רימן) [math]\displaystyle{ {\int\limits_D}_a^b f= }[/math] (לפי דרבו).

הוכחה[עריכה]

תחילה נניח ש-f אינטגרבילית לפי דרבו. נעיר שלכל חלוקה P ותת חלוקה P' של [math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ \underline S(f,P)\le S(f,P,P')\le\overline S(f,P) }[/math]. כעת נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math]. כיוון ש-f אינטגרבילית דרבו, [math]\displaystyle{ \overline S(f,P)\to{\int\limits_D}_a^b f }[/math] וכן [math]\displaystyle{ \underline S(f,P)\to{\int\limits_D}_a^b f }[/math] לכן משפט הסנדויץ' מבטיח ש-[math]\displaystyle{ \lim_{\lambda(P)\to0} S(f,P,P') }[/math] קיים ושווה ל-[math]\displaystyle{ {\int\limits_D}_a^b f }[/math]. ז"א f אינטגרבילית רימן ומתקיים [math]\displaystyle{ {\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P')={\int\limits_D}_a^b f }[/math].

לצד השני, נניח ש-f אינטגרבילית רימן. אזי מתקיים [math]\displaystyle{ {\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P') }[/math]. אם כן הוא גם שווה ל-[math]\displaystyle{ \lim_{\lambda(P)\to0} \sup_{P'} S(f,P,P')=\lim_{\lambda(P)\to0} \overline S(f,P)=\overline{\int}_a^b f }[/math],ובאופן דומה עבור אינטגרל תחתון (לפי דרבו, כמובן). מצאנו [math]\displaystyle{ {\int\limits_R}_a^b f=\overline{\int}_a^b f=\underline\int_a^b f }[/math]. עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם הוכחנו ש-[math]\displaystyle{ {\int\limits_R}_a^b f={\int\limits_D}_a^b f }[/math]. [math]\displaystyle{ \blacksquare }[/math]

משפט 11 (תכונות האינטגרל)[עריכה]

נניח ש-f ו-g מוגדרות ואינטגרביליות ב-[math]\displaystyle{ [a,b] }[/math], ונניח ש-c קבוע כלשהו. אזי:

(לינאריות): [math]\displaystyle{ f+cg }[/math] אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] ומתקיים [math]\displaystyle{ \int\limits_a^b(f+cg)=\int\limits_a^b f+c\int\limits_a^b g }[/math].
(מונוטוניות): אם [math]\displaystyle{ f(x)\ge g(x) }[/math] לכל [math]\displaystyle{ x\in[a,b] }[/math] אז [math]\displaystyle{ \int\limits_a^b f\ge\int\limits_a^b g }[/math]. (חיוביות): בפרט, אם [math]\displaystyle{ \forall x\in[a,b]:\ f(x)\ge0 }[/math] אז [math]\displaystyle{ \int\limits_a^b f\ge0 }[/math].
(הכללה לאי-שיוויון המשולש): |f| אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וגם [math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b |f| }[/math].
אם [math]\displaystyle{ m\le f(x)\le M }[/math] ב-[math]\displaystyle{ [a,b] }[/math] אז [math]\displaystyle{ m(b-a)\le\int\limits_a^b f\le M(b-a) }[/math] ואם [math]\displaystyle{ |f(x)|\le M }[/math] בקטע זה אז אז [math]\displaystyle{ \left|\int\limits_a^b f\right|\le M(b-a) }[/math].
אם [math]\displaystyle{ f(x)=M }[/math] (פונקציה קבועה) אז [math]\displaystyle{ \int\limits_a^b f= M(b-a) }[/math].

הוכחה[עריכה]

[math]\displaystyle{ S(f+cg,P,P')=\sum_{k=1}^n (f+cg)(c_k)\Delta x_k=\sum_{k=1}^n f(c_k)\Delta x_k+c\sum_{k=1}^n g(c_k)\Delta x_k }[/math]. נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math]. כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א [math]\displaystyle{ \lim_{\lambda(P)\to0} S(f+cg,P,P')=\int\limits_a^b f+c\int\limits_a^b g }[/math]. עצם קיום הגבול אומר ש-[math]\displaystyle{ f+cg }[/math] אינטגרבילית ולפי ערך הגבול נסיק [math]\displaystyle{ \int\limits_a^b (f+cg)=\int\limits_a^b f+c\int\limits_a^b g }[/math]. [math]\displaystyle{ \blacksquare }[/math]

את ההמשך עשינו בשיעור שאחריו:

נתבונן בסכום רימן כלשהו עבור g: [math]\displaystyle{ \sum_{k=1}^n g(c_k)\Delta x_k }[/math]. לפי הנתון הוא קטן או שווה ל- [math]\displaystyle{ \sum_{k=1}^n f(c_k)\Delta x_k }[/math]. נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math]. סכומים אלה שואפים לאינטגרלים של f ו-g ונסיק [math]\displaystyle{ \int\limits_a^b f\ge\int\limits_a^b g }[/math]. [math]\displaystyle{ \blacksquare }[/math]
נעיר ש-[math]\displaystyle{ \Omega }[/math] היא בעצם [math]\displaystyle{ \Omega(f)=\sup\{|f(x)-f(y)|:\ x,y\in[a,b]\} }[/math]. כזכור, אי שיוויון המשולש גורר ש-[math]\displaystyle{ \Big||f(x)|-|f(y)|\Big|\le|f(x)-f(y)| }[/math]. לכן [math]\displaystyle{ \Omega(|f|)=\sup_{x,y\in[a,b]}\Big||f(x)|-|f(y)|\Big|\le\sup_{x,y\in[a,b]}|f(x)-f(y)|=\Omega(f) }[/math]. כעת תהי P חלוקה כלשהי של [math]\displaystyle{ [a,b] }[/math] ואז [math]\displaystyle{ \overline S(f,P)-\underline S(f,P)=\sum_{k=1}^n (M_k(f)-m_k(f))\Delta x_k }[/math]. נעיר שלכל f, [math]\displaystyle{ M_k(f)-m_k(f) }[/math] היא התנודה של f בקטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] ולפי מה שהוכחנו זה גדול או שווה לתנודה של |f| באותו קטע:
[math]\displaystyle{ \begin{align}\overline S(f,P)-\underline S(f,P)&=\sum_{k=1}^n \Big(M_k(f)-m_k(f)\Big)\Delta x_k\\&\ge\sum_{k=1}^n \Big(M_k(|f|)-m_k(|f|)\Big)\Delta x_k\\&=\overline S(|f|,P)-\underline S(|f|,P)\end{align} }[/math]
כעת נוכיח ש-|f| אינטגרבילית. לצורך זה יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. כיוון ש-f אינטגרבילית (נתון) קיימת חלוקה P של [math]\displaystyle{ [a,b] }[/math] כך ש-[math]\displaystyle{ \overline S(|f|,P)-\underline S(|f|,P)\le\overline S(f,P)-\underline S(f,P)\to0 }[/math] ונובע ממשפט 5 ש-|f| אינטגרבילית. נותר להוכיח את אי-השיוויון [math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b |f| }[/math]. לפי אי-שיוויון המשולש, לכל סכום רימן של f מתקיים [math]\displaystyle{ \left|\sum_{k=1}^n f(c_k)\Delta x_k\right|\le\sum_{k=1}^n |f(c_k)|\Delta x_k }[/math]. נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math] ונקבל ש-[math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b|f| }[/math]. [math]\displaystyle{ \blacksquare }[/math]
נתון [math]\displaystyle{ m\le f(x)\le M }[/math]. לפי משפט 1, לכל חלוקה P של [math]\displaystyle{ [a,b] }[/math] מתקיים [math]\displaystyle{ m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a) }[/math]. נשאיף את [math]\displaystyle{ \lambda(P)\to0 }[/math] כדי להסיק [math]\displaystyle{ m(b-a)\le\int\limits_a^b f\le M(b-a) }[/math]. אם נתון [math]\displaystyle{ |f(x)|\le M }[/math] אז נוכל להסתמך על סעיף 3 ומה שהוכחנו הרגע לומר [math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b |f|\le M(b-a) }[/math]. [math]\displaystyle{ \blacksquare }[/math]
לפי הנתון [math]\displaystyle{ M\le f(x)\le M }[/math]. לכן, עפ"י סעיף 4 [math]\displaystyle{ M(b-a)\le\int\limits_a^b f\le M(b-a) }[/math] ויש שיוויון. [math]\displaystyle{ \blacksquare }[/math]