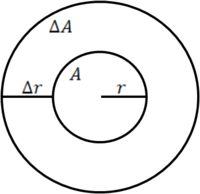משתמש:אור שחף/133 - הרצאה/27.3.11
< משתמש:אור שחף | 133 - הרצאה
יישומים של אינטגרציה (המשך)
-
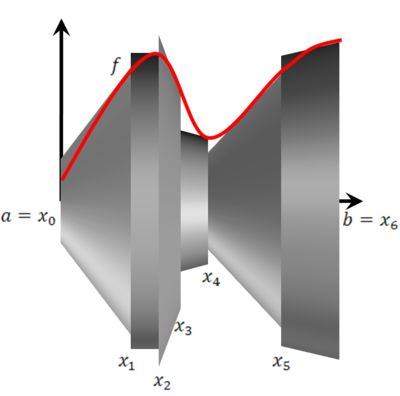
שטח המטעפת של גוף סיבוב (ללא הבסיסים)
נחלק את הקטע [math]\displaystyle{ [a,b] }[/math] לתתי קטעים [math]\displaystyle{ [x_{k-1},x_k] }[/math] עבור כמה k-ים ובכל קטע נחסום חרוט קטום (חרוט קטום הוא חרוט שהוסר ממנו הקודקוד ע"י "חיתוך" חלק בעזרת מישור המקביל לבסיס). שטח המעטפת של החרוט הקטום הוא [math]\displaystyle{ \pi(r_1+r_2)S }[/math] כאשר [math]\displaystyle{ r_1,r_2 }[/math] רדיוסי הבסיסים של החרוט הקטום הנוצר בקטע [math]\displaystyle{ [x_{k-1},x_k] }[/math], כלומר [math]\displaystyle{ f(x_k)-f'(x_k)\Delta x_k,f(x_k) }[/math] וכן [math]\displaystyle{ S=\sqrt{1+f'(x_k)^2}\Delta x_k }[/math] הוא אורך היוצר (יוצר של חרוט קטום הוא קו ישר המחבר בין נקודה על שפת אחד הבסיסים לנקודה הקרובה ביותר לה בשפת הבסיס השני). לפי זה שטח המעטפת כולו מקורב ע"י הסכום[math]\displaystyle{ \begin{align}&\sum_{k=1}^n\pi(2f(x_k)-f'(x_k)\Delta x_k)\sqrt{1+f'(x_k)^2}\Delta x_k=\\=&\sum_{k=1}^n2\pi f(x_k)\sqrt{1+f'(x_k)^2}\Delta x_k-\sum_{k=1}^n\pi f'(x_k)\sqrt{1+f'(x_k)^2}\Delta x_k^2\end{align} }[/math]כאשר [math]\displaystyle{ \lambda(P)\to0 }[/math] ביטוי זה שואף ל-[math]\displaystyle{ \int\limits_a^b2\pi f(x)\sqrt{1+f'(x)^2}\mathrm dx-0 }[/math] וזה שטח המעטפת לגוף הסיבוב הנוצר ע"י סיבוב [math]\displaystyle{ y=f(x) }[/math] בין a ל-b סביב ציר ה-x.דוגמה
נחשב את שטח המעטפת (השווה לשטח הפנים) של כדור בעל רדיוס r: מתקיים [math]\displaystyle{ f(x)=\sqrt{r^2-x^2} }[/math] ולכן [math]\displaystyle{ f'(x)=-\frac x\sqrt{r^2-x^2} }[/math]. השטח הוא[math]\displaystyle{ \begin{align}\int\limits_{-r}^r 2\pi f(x)\sqrt{1+f'(x)^2}\mathrm dx&=\int\limits_{-r}^r2\pi\sqrt{r^2-x^2}\sqrt{1+\frac{x^2}{r^2-x^2}}\mathrm dx\\&=\int\limits_{-r}^r2\pi\sqrt{r^2-x^2+x^2}\mathrm dx\\&=2\pi[rx]_{x=-r}^r\\&=4\pi r^2\end{align} }[/math][math]\displaystyle{ \blacksquare }[/math]
נשים לב כי שטח עיגול הוא [math]\displaystyle{ \pi r^2 }[/math] והיקפו [math]\displaystyle{ \frac{\mathrm d}{\mathrm dr}\pi r^2=2\pi r }[/math] כמו כן נפח כדור הוא [math]\displaystyle{ \frac43\pi r^3 }[/math] ושטחו [math]\displaystyle{ \frac{\mathrm d}{\mathrm dr}\frac43\pi r^3=4\pi r^2 }[/math]. נסביר זאת באמצעות הסרטוט משמאל. אם A הוא שטח המעגל הפנימי ו-[math]\displaystyle{ \Delta A }[/math] היא תוספת השטח הדרושה ליצירת המעגל החיצוני אזי [math]\displaystyle{ \Delta A\approx2\pi r\Delta r }[/math], ז"א [math]\displaystyle{ \frac{\Delta A}{\Delta r}\approx\frac{2\pi r\Delta r}{\Delta r}=2\pi r }[/math]. בגבול [math]\displaystyle{ \Delta r\to0 }[/math] זה מדוייק: [math]\displaystyle{ \frac{\mathrm dA}{\mathrm dr}=2\pi r }[/math]. ההסבר לכך שנגזרת נפח הכדור היא שטח הפנים דומה. לעומת זאת, עבור הריבוע
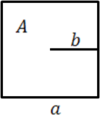ההיקף הוא [math]\displaystyle{ 4a }[/math] והשטח - [math]\displaystyle{ a^2 }[/math]: ההיקף אינו נגזרת השטח. אבל עבור [math]\displaystyle{ b=\frac a2 }[/math] ההיקף הינו [math]\displaystyle{ 8b }[/math] והשטח - [math]\displaystyle{ 4b^2 }[/math], ושוב ההיקף הוא נגזרת השטח.
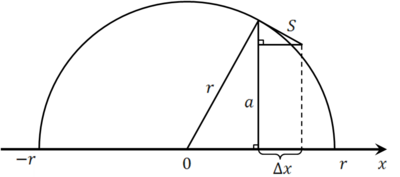
נחשב שטח פנים של כדור ללא אינטגרל: עפ"י דימיון משולשים [math]\displaystyle{ \frac ar=\frac{\Delta x}S }[/math] ולכן [math]\displaystyle{ aS=r\Delta x }[/math]. אותה חתיכת הגרף S מסתובבת סביב ציר ה-x ליצור שטח [math]\displaystyle{ \pi\left(2a-\sqrt{S^2-(\Delta x)^2}\right)S=2\pi r\Delta x-\pi S\sqrt{S^2-(\Delta x)^2} }[/math] (כי רדיוסי הבסיסים של החרוט הקטום הם [math]\displaystyle{ a,a-\sqrt{S^2-(\Delta x)^2} }[/math]). ז"א, בכל קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] שבו נבנה חרוט קטום ע"י סיבוב קו באורך [math]\displaystyle{ S }[/math] יווצר שטח [math]\displaystyle{ 2\pi r\Delta x_k-\pi S\sqrt{S^2-(\Delta x_k)^2} }[/math]. כעת, אם נסכם אינסוף קטעים לאורך הקטע [math]\displaystyle{ [-r,r] }[/math] כך שלכל קטע [math]\displaystyle{ \Delta x_k\to0 }[/math] יבנה שטח כולל [math]\displaystyle{ 2\pi r\sum\Delta x-\sum0=2\pi r(r-(-r))=4\pi r^2 }[/math], כפי שציפינו.
-
חישוב עבודה
בפיזיקה, כאשר כוח [math]\displaystyle{ \vec F }[/math] קבוע פועל בקטע באורך s אומרים שהוא עשה עבודה [math]\displaystyle{ W=\vec Fs }[/math]. כעת נחשב את העבודה שנעשית ע"י כוח משתנה [math]\displaystyle{ F(x) }[/math] לאורך הקטע [math]\displaystyle{ x\in[a,b] }[/math] בציר הזמן. נעשה חלוקה [math]\displaystyle{ P=\{x_0,x_1,\dots,x_n\} }[/math]. בכל תת קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math], [math]\displaystyle{ F(x) }[/math] תקבל מקסימום [math]\displaystyle{ M_k }[/math] ומינימום [math]\displaystyle{ m_k }[/math] ולכן העבודה הנעשית ע"י F בקטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] (נקרא לה [math]\displaystyle{ W_k }[/math]) מקיימת [math]\displaystyle{ m_k\Delta x_k\le W_k\le M_k\Delta x }[/math]. בסה"כ העבודה לאורך הקטע היא [math]\displaystyle{ W=\sum_{k=1}^n W_k }[/math] כאשר [math]\displaystyle{ \sum_{k=1}^n m_k\Delta x_k\le W\le\sum_{k=1}^n M_k\Delta x_k }[/math]. יש כאן [math]\displaystyle{ \underline S(F,P)\le W\le \overline S(F,P) }[/math] וכאשר [math]\displaystyle{ \lambda(P)\to0 }[/math] זה שואף לגבול אחד [math]\displaystyle{ W=\int\limits_a^b F(x)\mathrm dx }[/math].
-
העבודה שווה לשינוי באנרגיה הקינטית
החוק השני של ניוטון אומר [math]\displaystyle{ F=ma }[/math] ואם מדובר בחלקיק או אדם שהולך בקו ישר (על ציר ה-x) אז התנועה שלו מתוארת ע"י הפונקציה [math]\displaystyle{ x=x(t) }[/math] (לכל t נקודה בזמן). לפיכך מהירותו היא [math]\displaystyle{ v(t)=\frac{\mathrm dx}{\mathrm dt} }[/math] ותאוצתו [math]\displaystyle{ a(t)=\frac{\mathrm dv}{\mathrm dt}=\frac{\mathrm d^2x}{\mathrm dt^2} }[/math]. לפי ניוטון [math]\displaystyle{ F=ma=m\frac{\mathrm dv}{\mathrm dt} }[/math]. לפי כלל השרשרת אפשר לכתוב [math]\displaystyle{ \frac{\mathrm dv}{\mathrm dt}=\frac{\mathrm dx}{\mathrm dt}\cdot\frac{\mathrm dv}{\mathrm dx} }[/math] ולכן [math]\displaystyle{ F=m\frac{\mathrm dv}{\mathrm dx}v }[/math]. לכן העבודה שנעשית ע"י [math]\displaystyle{ F(x) }[/math] בין a ל-b היא[math]\displaystyle{ \begin{align}W&=\int\limits_a^b F(x)\mathrm dx\\&=\int\limits_a^b m\frac{\mathrm dv}{\mathrm dx}v\mathrm dx\\&=\left[\frac{mv^2}2\right]_{x=a}^b\end{align} }[/math]ז"א העבודה שווה לשינוי באינרגיה הקינטית.הסבר לנוסחה [math]\displaystyle{ \frac{\mathrm dv}{\mathrm dt}=\frac{\mathrm dx}{\mathrm dt}\cdot\frac{\mathrm dv}{\mathrm dx} }[/math]: כאן מניחים ש-[math]\displaystyle{ x(t)=x }[/math] ו-[math]\displaystyle{ v(x)=v }[/math]. בזה נוצרת פונקציה מרוכבת [math]\displaystyle{ v(x(t)) }[/math]. למדנו את כלל השרשרת [math]\displaystyle{ \frac{\mathrm d}{\mathrm dt}v(x(t))=v'(x(t))x'(t) }[/math] כלומר [math]\displaystyle{ \frac{\mathrm dv}{\mathrm dt}=\frac{\mathrm dx}{\mathrm dt}\cdot\frac{\mathrm dv}{\mathrm dx} }[/math].
מבוא לאינטגרציה נומרית
נביא כאן 4 שיטות לקירוב של אינטגרל מסוים:
אינטגרציה בעזרת פיתוח טיילור
לדוגמה, נחשב [math]\displaystyle{ \int\limits_0^1 e^{x^2}\mathrm dx }[/math] בדיוק של [math]\displaystyle{ 10^{-6} }[/math]: כבר למדנו פיתוח טיילור לפונקציה [math]\displaystyle{ e^t }[/math]: [math]\displaystyle{ e^t=1+t+\frac{t^2}{2!}+\frac{t^3}{3!}+\dots+\frac{t^n}{n!}+R_n(t) }[/math] כאשר [math]\displaystyle{ R_n(t)=\frac{f^{(n+1)}(c)t^{n+1}}{(n+1)!}=\frac{e^ct^{n+1}}{(n+1)!} }[/math] לאיזה c בין 0 ל-t. נציב [math]\displaystyle{ t=x^2 }[/math]: [math]\displaystyle{ e^{x^2}=1+x^2+\frac{x^4}{2!}+\frac{x^6}{3!}+\dots+\frac{x^{2n}}{n!}+R_n\left(x^2\right) }[/math]. לכן [math]\displaystyle{ \int\limits_0^1 e^{x^2}\mathrm dx=\int\limits_0^1 P_n\left(x^2\right)\mathrm dx+\int\limits_0^1 R_n\left(x^2\right)\mathrm dx }[/math]. אנו זקוקים ל-n כך ש-[math]\displaystyle{ \left|\int\limits_0^1 R_n\left(x^2\right)\mathrm dx\right|=\left|\int\limits_0^1\frac{e^cx^{2n+2}}{(n+1)!}\right|\lt 10^{-6} }[/math]. לכל [math]\displaystyle{ x\in[0,1] }[/math] מתקיים [math]\displaystyle{ e^0\le e^c\le e^1\lt 3 }[/math] ולכן השארית חסומה ע"י [math]\displaystyle{ 3\left|\int\limits_0^1\frac{x^{2n+2}}{(n+1)!}\mathrm dx\right|=\frac3{(2n+3)(n+1)!} }[/math]. אכן, עבור [math]\displaystyle{ n=7 }[/math] זה מספיק קטן. לפי זה[math]\displaystyle{ \begin{align}\int\limits_0^1 e^{x^2}\mathrm dx&\approx\int\limits_0^1\left(1+x^2+\frac{x^4}{2!}+\frac{x^6}{3!}+\frac{x^8}{4!}+\frac{x^{10}}{5!}+\frac{x^{12}}{6!}+\frac{x^{14}}{7!}\right)\mathrm dx\\&=\dots\\&\approx1.4626501\end{align} }[/math]השיטה הזאת לא תמיד מועילה כי- לא כל פונקציה גזירה מספיק פעמים כדי שנוכל לחשב [math]\displaystyle{ P_n(x) }[/math] ל-n גדול די הצורך.
- יש פונקציות בעלות אינסוף נגזרות שפשוט לא מקורבות היטב ע"י פיתוח טיילור, ובפרט על קטע ארוך.
- יש פונקציות שקשה לחשב את פיתוח טיילור שלהן כי הוא תלוי בנגזרת מסדר גבוה.
קירוב עפ"י סכומי רימן
נניח ש-f רציפה בקטע [math]\displaystyle{ [a,b] }[/math]. נקח [math]\displaystyle{ n\in\mathbb N }[/math] כלשהו ונעשה חלוקה שווה של [math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math] כאשר לכל k נגדיר [math]\displaystyle{ h=\frac{b-a}n=x_k-x_{k-1} }[/math] (כאשר h הוא אורך הפסיעה בין שתי נקודות החלוקה). הקירוב לאינטגרל נתון ע"י סכום רימן [math]\displaystyle{ \sum_{k=1}^n f(x_k)\Delta x_k=h\sum_{k=1}^n f(x_k) }[/math]. כעת נניח ש-f בעלת נגזרת רציפה [math]\displaystyle{ f' }[/math] ב-[math]\displaystyle{ [a,b] }[/math] ונחשב את סדר גודל הטעות בקירוב הנ"ל: מתקיים [math]\displaystyle{ \int\limits_a^b f(x)\mathrm dx=\sum_{k=1}^n\int\limits_{x_{k-1}}^{x_k} f(x_k)\mathrm dx }[/math]. בתוך הקטע הקטן [math]\displaystyle{ [x_{k-1},x_k] }[/math] נסתמך על משפט לגראנז' לומר [math]\displaystyle{ f'(c)=\frac{f(x)-f(x_k)}{x-x_k} }[/math] עבור c בין x ל-[math]\displaystyle{ x_k }[/math]. נעביר אגף לומר [math]\displaystyle{ f(x)=f(x_k)+f'(c)(x-x_k) }[/math] ולכן [math]\displaystyle{ \int\limits_{x_{k-1}}^{x_k} f(x_k)\mathrm dx+\int\limits_{x_{k-1}}^{x_k} f'(c)(x-x_k)\mathrm dx=f(x_k)(x_k-x_{k-1})+R_k }[/math]. [math]\displaystyle{ f(x_k)h }[/math] היא התרומה של קטע זה לסכום רימן ו-[math]\displaystyle{ R_k=\int\limits_{x_{k-1}}^{x_k} f'(c)(x-x_k)\mathrm dx }[/math] הוא הטעות. כעת, אם נסמן [math]\displaystyle{ M=\max_{x\in[a,b]}\left|f'(x)\right| }[/math] נוכל להסיק[math]\displaystyle{ \begin{align}|R_k|&=\left|\int\limits_{x_{k-1}}^{x_k} f'(c)(x-x_k)\mathrm dx\right|\\&=\left|f'(c)\right|\int\limits_{x_{k-1}}^{x_k} (x_k-x)\mathrm dx\\&\le\frac{Mh^2}2\end{align} }[/math]יש בסה"כ n קטעים כאלה ולכן השארית הכללית חסומה ע"י [math]\displaystyle{ \sum_{k=1}^n |R_k|\le n\frac{Mh^2}2=\frac{b-a}{2h}Mh^2=\frac{b-a}2 Mh }[/math].