משתמש:אור שחף/133 - תרגול/3.4.11

שימושי האינטגרל

דוגמה 1

חשבו את השטח הכלוא ע"י הישר [math]\displaystyle{ y=4x }[/math] והפרבולה [math]\displaystyle{ y=(2x-4)^2 }[/math].

פתרון

נצייר את הגרף (1) של הפונקציות ונמצא את 2 נקודות החיתוך: [math]\displaystyle{ (2x-4)^2=4x\implies x^2-5x+4=0\implies x=1,4 }[/math].

• דרך 1: נסובב את מערכת הצירים ב-[math]\displaystyle{ 90^\circ }[/math] ונקבל גרף (2). עתה נחשב את השטח בין [math]\displaystyle{ y^2=4x\implies x=\frac{y^2}4 }[/math] וכן [math]\displaystyle{ y=2x-4\implies x=\frac12y+2 }[/math]. קל לראות שהישר מעל הפרבולה, אבל גם אם לא כך אז הסימן של התוצאה יהא הפוך. לכן ניקח ערך מוחלט. שיעורי ה-y של נקודות החיתוך הם [math]\displaystyle{ -2,4 }[/math] (לפי שיעורי ה-x) ולכן השטח הוא [math]\displaystyle{ \left|\int\limits_{-2}^4\left(\frac y2+2-\frac{y^2}4\right)\mathrm dy\right|=\left|\left[\frac{y^2}4+2y-\frac{y^3}{12}\right]_{y=-2}^4\right|=9 }[/math].
• דרך 2: נפרק לשלושה שטחים: השטח [math]\displaystyle{ S_1 }[/math] בין [math]\displaystyle{ x=1 }[/math] ל-4 ושני שטחים שווים [math]\displaystyle{ S_2=S_3 }[/math] בין 0 ל-1, שטח אחד מעל ציר ה-x והשני מתחת. לפיכך השטח הכולל הוא [math]\displaystyle{ S_1+2S_2=\left|\int\limits_1^4\left(\sqrt{4x}-2x+4\right)\mathrm dx\right|+2\left|\int\limits_0^1\sqrt{4x}\mathrm dx\right|=9 }[/math]

דוגמה 2

חשבו את השטח הכלוא בין הגרפים של הפונקציות [math]\displaystyle{ y=e^x,\ y=2-\frac1{e^x},\ y=0,\ x=-1 }[/math].

פתרון

נקודות חיתוך:

• [math]\displaystyle{ y=e^x,\ y=2-\frac1{e^x}\implies x=0 }[/math]
• [math]\displaystyle{ y=2-\frac1{e^x},\ y=0\implies x=-\ln(2) }[/math]
• ברור כי ל-[math]\displaystyle{ y=e^x,\ y=0 }[/math] אין נקודת חיתוך.

לכן השטח הוא [math]\displaystyle{ \left|\int\limits_{-1}^{-\ln(2)} e^x\mathrm dx\right|+\left|\int\limits_{-\ln(2)}^0\left(e^x-2+e^{-x}\right)\mathrm dx\right|=2-\ln(4)-\frac1e }[/math].

דוגמה 3

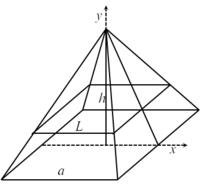
מצאו נוסחה לחישוב נפח של פירמידה ישרה אשר גובהה h ובסיסה ריבוע שאורך צלעו a.

פתרון

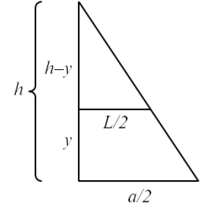
נבחר את מערכת הצירים כך שקודקוד הפירמידה עובר דרך ציר ה-y וציר ה-y מאונך לבסיסה. יוצא שציר ה-x מונח במישור על בסיס הפירמידה ומקביל/מאונך לצלעותיו. לכל קטע מהצורה [math]\displaystyle{ [0,y] }[/math] החתך הניצב לציר ה-y הוא ריבוע. נסמן ב-L את אורך הצלע של ריבוע זה. מדמיון משושלים נקבל [math]\displaystyle{ \frac{L/2}{a/2}=\frac{h-y}h\implies L=\frac{h-y}h\cdot a }[/math] ולכן שטח חתך כזה הוא [math]\displaystyle{ S(L)=\left(\frac{h-y}h\cdot a\right)^2 }[/math]. נזכור שהחתך נפרס לרוחב, כלומר השמתנה שלנו הוא y, וידוע שהוא רץ בין 0 ל-h. אם נקח לכל חתך כזה תיבה שבסיסה הוא החתך וגובהה שואף ל-0 ונחבר את נפחי התיבות נקבל את נפח הפירמידה. לכן הנפח הוא [math]\displaystyle{ \int\limits_0^h S(L)\mathrm dy=\int\limits_0^h\frac{(y-h)^2}{h^2}\cdot a^2\mathrm dy=\frac{a^2}{h^2}\left[\frac{(y-h)^3}3\right]_{y=0}^h=\frac{a^2h}3 }[/math].

נפח גוף סיבוב

נפח גוף סיבוב סביב ציר ה-x מתקבל ע"י הנוסחה [math]\displaystyle{ V=\int\limits_a^b\pi(f(x))^2\mathrm dx }[/math].

דוגמה 4

חשבו את הנפח הנוצר ע"י סיבוב הפרבולה [math]\displaystyle{ y^2=8x }[/math] סביב ציר ה-x, עד לישר [math]\displaystyle{ x=2 }[/math].

פתרון

[math]\displaystyle{ y^2=8x\implies y=\pm\sqrt{8x} }[/math]. מכיוון שעם סיבוב הרביע הראשון מתקבל הרביע הרביעי מספיק לחשב את נפח גוף הסיבוב של [math]\displaystyle{ \sqrt{8x} }[/math] בין 0 ל-2. לכן, לפי הנוסחה, [math]\displaystyle{ V=\int\limits_0^2\pi\left(\sqrt{8x}\right)^2\mathrm dx=8\pi\left[\frac{x^2}2\right]_{x=0}^2=16\pi }[/math].

דוגמה 5

מצאו נוחה לחישוב נפח של כדור שרדיוסו r.

פתרון

ע"מ לחשב את הנוסחה נוכל לסובב את חציו העליון של עיגול. לפי נוסחת מעגל [math]\displaystyle{ x^2+y^2=r^2 }[/math] ולכן בחצי המישור העליון [math]\displaystyle{ y=\sqrt{r^2-x^2} }[/math]. הנפח הוא [math]\displaystyle{ \int\limits_{-r}^r\pi\left(\sqrt{r^2-x^2}\right)^2\mathrm dx=\pi\int\limits_{-r}^r\left(r^2-x^2\right)\mathrm dx=\frac43\pi r^3 }[/math].

דוגמה 6

מצאו את נפח הגוף שנוצר כאשר מסובבים את התחום הכלוא בין הגרפים [math]\displaystyle{ f(x)=\frac12+x^2 }[/math] ו-[math]\displaystyle{ g(x)=x }[/math] בקטע [math]\displaystyle{ [0,2] }[/math].

פתרון

נמצא את שיעורי ה-x של נקודות החיתוך: [math]\displaystyle{ \frac12+x^2=x\implies x\not\in\mathbb R }[/math], כלומר אין נקודות חיתוך. לפיכך הנפח הוא [math]\displaystyle{ \int\limits_0^2\pi\left((f(x))^2-(g(x))^2\right)\mathrm dx=\pi\int\limits_0^2\left(\left(x^2+\frac12\right)^2-x^2\right)\mathrm dx=\dots=\frac{69}{10}\pi }[/math].

---

נפח גוף סיבוב המסתובב סביב ציר ה-y במקום ציר ה-x בקטע [math]\displaystyle{ [a,b] }[/math] נתון ע"י הנוסחה [math]\displaystyle{ V=2\pi\int\limits_a^b xf(x)\mathrm dx }[/math].

דוגמה 7

חשבו הנפח הנוצר מסיבוב התחום הנקבע ע"י [math]\displaystyle{ y=\sqrt x,\ x=1,\ x=4 }[/math] סביב ציר ה-y.

פתרון

לפי הנוסחה [math]\displaystyle{ V=2\pi\int\limits_1^4\sqrt x^3\mathrm dx=2\pi\left[\frac{x^{5/2}}{5/2}\right]_{x=1}^4=\frac{124}5\pi }[/math].

דוגמה 8

חשב את נפח התחום שמתחת ל-[math]\displaystyle{ y=x^2 }[/math] בקטע [math]\displaystyle{ [0,2] }[/math] המסתובב סביב ציר ה-x.

פתרון

[math]\displaystyle{ \int\limits_0^2\pi x^4\mathrm dx=\frac{32}5\pi }[/math].