משתמש:אור שחף/133 - תרגול/15.5.11: הבדלים בין גרסאות בדף
(יצירת דף עם התוכן "=התכנסות במ"ש {{הערה|(המשך)}}= '''משפט:''' <math>f_n\to f</math> במ"ש בקטע I אם"ם לכל <math>\varepsilon>0</math> יש <math>n_0\i...") |
אין תקציר עריכה |
||
| (גרסת ביניים אחת של אותו משתמש אינה מוצגת) | |||
| שורה 3: | שורה 3: | ||
==דוגמה 1== | ==דוגמה 1== | ||
תהי <math>f_n(x)=\ln\left(x+\frac{x^2}n\right)</math>. קבעו התכנסות בכל אחד מהקטעים הבאים: | תהי <math>f_n(x)=\ln\left(x+\frac{x^2}n\right)</math>. קבעו התכנסות בכל אחד מהקטעים הבאים: | ||
# <math>[a,b]</math> עבור <math>b | # <math>[a,b]</math> עבור <math>0<a<b<\infty</math> | ||
# בקטע <math>(0,\infty)</math> | # בקטע <math>(0,\infty)</math> | ||
===פתרון=== | ===פתרון=== | ||
פונקציית הגבול היא <math>\lim_{n\to\infty}\ln\left(x+\frac{x^2}n\right)=\ln(x+0)=\ln(x)</math>. | פונקציית הגבול היא <math>\lim_{n\to\infty}\ln\left(x+\frac{x^2}n\right)=\ln(x+0)=\ln(x)</math>. | ||
# נראה התכנסות במ"ש ב-<math>[a,b]</math>: <math>\sup_{x\in[a,b]}\left|\ln\left(x+\frac{x^2}n\right)-\ln(x)\right|=\sup_{n\in[a,b]}\left|\ln\left(1+\frac xn\right)\right|=\ln\left(1+\frac bn\right)\to0</math>. {{משל}} | # נראה התכנסות במ"ש ב-<math>[a,b]</math>: <math>\sup_{x\in[a,b]}\left|\ln\left(x+\frac{x^2}n\right)-\ln(x)\right|=\sup_{n\in[a,b]}\left|\ln\left(1+\frac xn\right)\right|=\ln\left(1+\frac bn\right)\to0</math>. {{משל}} | ||
# נראה שההתכנסות נקודתית בלבד ב-<math>(0,\infty)</math>: <math>\sup_{x\in(0,\infty)}|f_n(x)-f(x)|=\sup_{x\in(0,\infty)}\left|\ln\left(1+\frac xn\right)\right| | # נראה שההתכנסות נקודתית בלבד ב-<math>(0,\infty)</math>: <math>\sup_{x\in(0,\infty)}|f_n(x)-f(x)|=\sup_{x\in(0,\infty)}\left|\ln\left(1+\frac xn\right)\right|=\infty</math>. {{משל}} | ||
==דוגמה 2== | ==דוגמה 2== | ||
קבע האם <math>f_n(x)=\frac1{1+n^2x^2}</math> מתכנסת במ"ש ב-<math>(-\infty,\infty)=\mathbb R</math>. | קבע האם <math>f_n(x)=\frac1{1+n^2x^2}</math> מתכנסת במ"ש ב-<math>(-\infty,\infty)=\mathbb R</math>. | ||
===פתרון=== | ===פתרון=== | ||
קל לראות ש-<math>f(x)=\lim_{n\to\infty}f_n(x)=\begin{cases}1&x=0\\0&\text{else}\end{cases}</math>. נבדוק התכנסות במ"ש: <math>\sup_{x\in\mathbb R}|f_n(x)-f(x)|\ge\sup_{x\in\mathbb R}|f_n(x)|=\ | קל לראות ש-<math>f(x)=\lim_{n\to\infty}f_n(x)=\begin{cases}1&x=0\\0&\text{else}\end{cases}</math>. נבדוק התכנסות במ"ש: <math>\sup_{x\in\mathbb R}|f_n(x)-f(x)|\ge\sup_{x\in\mathbb R}|f_n(x)|=\left|\sup_{x\in\mathbb R}\frac1{1+n^2x^2}\right|=\left|\sup_{x\in[0,\infty)}\frac1{1+n^2x^2}\right|</math>. נחפש מקסימום: <math>f_n'(x)=\frac{-2n^2x}{\left(1+n^2x^2\right)^2}=0</math> וקל לראות שהנגזרת מתאפסת עבור <math>x=0</math>. ברור ש-<math>f_n</math> מונוטונית יורדת ב-<math>[0,\infty)</math> ולכן זו אכן נקודת מקסימום גלובלית. מתקיים <math>f_n(0)=1</math> ולכן <math>\sup_{x\in\mathbb R}|f_n(x)-f(x)|\ge1\not\to0</math>. מכאן שההתכנסות נקודתית בלבד. {{משל}} | ||
==דוגמה 3== | ==דוגמה 3== | ||
תהי <math>\{f_n\}</math> סדרת פונקציות המתכנסת במ"ש לפונקציה f, האם f חסומה? | תהי <math>\{f_n\}</math> סדרת פונקציות המתכנסת במ"ש לפונקציה f, האם f חסומה? | ||
===פתרון=== | ===פתרון=== | ||
נבחר לדוגמה <math>f_n(x)=\frac1x+\frac1n</math> בקטע <math>(0,\infty)</math>. ברור כי <math>f(x)=\lim_{n\to\infty}f_n(x)=\frac1x</math> וכי אם <math>x\to0^+</math> אז <math>\frac1x\to\infty</math>, לכן f לא חסומה. | נבחר לדוגמה <math>f_n(x)=\frac1x+\frac1n</math> בקטע <math>(0,\infty)</math>. ברור כי <math>f(x)=\lim_{n\to\infty}f_n(x)=\frac1x</math> וכי אם <math>x\to0^+</math> אז <math>\frac1x\to\infty</math>, לכן f לא חסומה. {{משל}} | ||
==דוגמה 4== | ==דוגמה 4== | ||
תהי <math>f_n</math> סדרת פונקציות המתכנסת לפונקציה f במ"ש ב-I. נוכיח כי אם כל אחת מהפונקציות <math>f_n</math> חסומה ב-I, אזי גם f חסומה ב-I. | תהי <math>\{f_n\}</math> סדרת פונקציות המתכנסת לפונקציה f במ"ש ב-I. נוכיח כי אם כל אחת מהפונקציות <math>f_n</math> חסומה ב-I, אזי גם f חסומה ב-I. | ||
===פתרון=== | ===פתרון=== | ||
נרשום <math>|f|\le|f-f_n|+|f_n|</math>. נתון כי ההתכנסות במ"ש ולכן <math>\forall\varepsilon>0:\ \exists n_0:\ \forall n>n_0:\ |f(x)-f_n(x)| | נרשום <math>|f|\le|f-f_n|+|f_n|</math>. נתון כי ההתכנסות במ"ש ולכן <math>\forall\varepsilon>0:\ \exists n_0:\ \forall n>n_0:\ |f(x)-f_n(x)|<\varepsilon</math>, בפרט עבור <math>\varepsilon=1</math>. כמו כן <math>f_{n_0+1}</math> חסומה ב-I (מהנתון) כלומר קיים M כך ש-<math>\sup_{x\in I}|f_{n_0+1}(x)|\le M<\infty</math> ולכן מתקבל ש-<math>|f(x)|\le1+|f_{n_0+1}(x)|<1+M</math> לכל <math>x\in I</math>. {{משל}} | ||
| שורה 32: | שורה 32: | ||
==דוגמה 5== | ==דוגמה 5== | ||
ניתן דוגמה לסדרת פונקציות רציפות המתכנסות לפונקציה רציפה אבל לא מתכנסת במ"ש | ניתן דוגמה לסדרת פונקציות רציפות המתכנסות לפונקציה רציפה אבל לא מתכנסת במ"ש. | ||
===פתרון=== | ===פתרון=== | ||
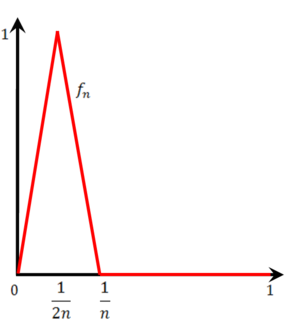
נגדיר את הפונקציה הבאה: <math>f_n(x)=\begin{cases}2nx&0\le x\le\frac1{2n}\\2-2nx&\frac1{2n}<x\le\frac1n\\0&\frac1n<x\le1\end{cases}</math>. קל לראות שהפונקציה הנ"ל מוגדרת בקטע <math>[0,1]</math>, אפשר לראות שהפונקציה הנ"ל רציפה. | [[קובץ:פונקציה בין 0 ל-1.png|ממוזער|300px|ימין]] | ||
נגדיר את הפונקציה הבאה: <math>f_n(x)=\begin{cases}2nx&0\le x\le\frac1{2n}\\2-2nx&\frac1{2n}<x\le\frac1n\\0&\frac1n<x\le1\end{cases}</math>. קל לראות שהפונקציה הנ"ל מוגדרת בקטע <math>[0,1]</math>, אפשר לראות שהפונקציה הנ"ל רציפה. | |||
לכל <math>x_0</math> יש <math>n_0</math> כך שלכל <math>n>n_0</math> מתקיים <math>x_0>\frac1{n_0}</math> שם מתקיים <math>f_n(x_0)=0</math>, כלומר <math>\{f_n(x_0)\}</math> סדרה קבועה מ-<math>n_0</math> מסויים. כמו כן <math>\sup_{x\in[0,1]}|f_n(x)-f(x)|=1</math> ולכן ההתכנסות אינה במ"ש. | לכל <math>x_0</math> יש <math>n_0</math> כך שלכל <math>n>n_0</math> מתקיים <math>x_0>\frac1{n_0}</math> שם מתקיים <math>f_n(x_0)=0</math>, כלומר <math>\{f_n(x_0)\}</math> סדרה קבועה מ-<math>n_0</math> מסויים. כמו כן <math>\sup_{x\in[0,1]}|f_n(x)-f(x)|=1</math> ולכן ההתכנסות אינה במ"ש. | ||
=טורים של פונקציות= | =טורים של פונקציות= | ||
==דוגמה 6== | ==דוגמה 6== | ||
נסמן | נסמן לכל n, <math>f_n(x)=x^{n-1}</math> בקטע <math>(-1,1)</math>. מה היא פונקצית הסכום <math>S_N</math>? | ||
===פתרון=== | ===פתרון=== | ||
<math>S_N(x)=\sum_{n=1}^N f_n(x)=1+x+\dots+x^{N-1}=\frac{1-x^N}{1-x}\to\frac1{1-x}</math>. | <math>S_N(x)=\sum_{n=1}^N f_n(x)=1+x+\dots+x^{N-1}=\frac{1-x^N}{1-x}\to\frac1{1-x}</math>. | ||
| שורה 49: | שורה 47: | ||
נוכיח כי הטור <math>S_N(x)=\sum_{n=0}^N\frac{(-1)^nx^{2n+1}}{(2n+1)!}</math> מתכנס ל-<math>\sin(x)</math> במ"ש בקטע <math>[0,2\pi]</math> כאשר <math>n\to\infty</math>. | נוכיח כי הטור <math>S_N(x)=\sum_{n=0}^N\frac{(-1)^nx^{2n+1}}{(2n+1)!}</math> מתכנס ל-<math>\sin(x)</math> במ"ש בקטע <math>[0,2\pi]</math> כאשר <math>n\to\infty</math>. | ||
===פתרון=== | ===פתרון=== | ||
ברור שיש התכנסות נקודתית, נותר לבדוק התכנסות במ"ש. נסמן <math>f_n(x)=\frac{(-1)^nx^{2n+1}}{(2n+1)!}</math>. מתקיים <math>|S_N(x)-\sin(x)| | בזכות טורי טיילור ברור שיש התכנסות נקודתית, נותר לבדוק התכנסות במ"ש. נסמן <math>f_n(x)=\frac{(-1)^nx^{2n+1}}{(2n+1)!}</math>. כאשר <math>R_N(x)</math> השארית בין הטור-טיילור מסדר N לבין <math>\sin</math> מתקיים <math>|S_N(x)-\sin(x)|=|R_N(x)|\le\left|\frac{x^{2(N+1)+1}}{(2(N+1)+1)!}\right|</math>. כמו כן <math>\frac{x^{2N+3}}{(2N+3)!}\le\frac{(2\pi)^{2N+3}}{(2N+3)!}=:a_N</math>. נוכיח ש-<math>a_N\to0</math> וכך נוכיח שההתכנסות במ"ש. מספיק להסתכל על <math>\left|\frac{a_{N+1}}{a_N}\right|=\frac{(2\pi)^{2N+5}}{(2N+5)!}\frac{(2N+3)!}{(2\pi)^{2N+3}}=\frac{(2\pi)^2}{(2N+4)(2N+5)}\to0</math>, לכן <math>\sum_{n=1}^\infty a_n</math> מתכנס ובפרט <math>a_n\to0</math>. {{משל}} | ||
==דוגמה 8== | ==דוגמה 8== | ||
בדקו התכנסות במ"ש <math>\sum_{n=1}^\infty \frac{\cos(nx)}{n^2}</math>. | בדקו התכנסות במ"ש של <math>\sum_{n=1}^\infty \frac{\cos(nx)}{n^2}</math>. | ||
===פתרון=== | ===פתרון=== | ||
נשים לב כי לא | נשים לב כי לא ידועה לנו פונקצית הגבול של הטור ולכן לא ניתן להוכיח התכנסות במ"ש ישירות מההגדרה. במקום, נפנה לתנאי קושי: יהי <math>\varepsilon>0</math> נתון. ברור כי <math>\left|\sum_{k=n}^m\frac{\cos(kx)}{k^2}\right|\le\left|\sum_{k=n}^m\frac1{k^2}\right|</math>. הטור <math>\sum_{k=1}^\infty\frac1{k^2}</math> מתכנס ולכן מקיים את תנאי קושי, כלומר קיים <math>n_0\in\mathbb N</math> כל שלכל <math>m>n>n_0</math> מתקיים <math>\left|\sum_{k=n}^m\frac1{k^2}\right|<\varepsilon</math>. לכן, עבור אותו <math>n_0</math>, לכל <math>m>n>n_0</math> מתקיים <math>\left|\sum_{k=n}^m\frac{\cos(kx)}{k^2}\right|<\varepsilon</math>. {{משל}} | ||
גרסה אחרונה מ־17:24, 8 ביוני 2011
התכנסות במ"ש (המשך)
משפט: [math]\displaystyle{ f_n\to f }[/math] במ"ש בקטע I אם"ם לכל [math]\displaystyle{ \varepsilon\gt 0 }[/math] יש [math]\displaystyle{ n_0\in\mathbb N }[/math] כך שלכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ \sup_{x\in I}|f_n(x)-f(x)|\lt \varepsilon }[/math].
דוגמה 1
תהי [math]\displaystyle{ f_n(x)=\ln\left(x+\frac{x^2}n\right) }[/math]. קבעו התכנסות בכל אחד מהקטעים הבאים:
- [math]\displaystyle{ [a,b] }[/math] עבור [math]\displaystyle{ 0\lt a\lt b\lt \infty }[/math]
- בקטע [math]\displaystyle{ (0,\infty) }[/math]
פתרון
פונקציית הגבול היא [math]\displaystyle{ \lim_{n\to\infty}\ln\left(x+\frac{x^2}n\right)=\ln(x+0)=\ln(x) }[/math].
- נראה התכנסות במ"ש ב-[math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ \sup_{x\in[a,b]}\left|\ln\left(x+\frac{x^2}n\right)-\ln(x)\right|=\sup_{n\in[a,b]}\left|\ln\left(1+\frac xn\right)\right|=\ln\left(1+\frac bn\right)\to0 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- נראה שההתכנסות נקודתית בלבד ב-[math]\displaystyle{ (0,\infty) }[/math]: [math]\displaystyle{ \sup_{x\in(0,\infty)}|f_n(x)-f(x)|=\sup_{x\in(0,\infty)}\left|\ln\left(1+\frac xn\right)\right|=\infty }[/math]. [math]\displaystyle{ \blacksquare }[/math]
דוגמה 2
קבע האם [math]\displaystyle{ f_n(x)=\frac1{1+n^2x^2} }[/math] מתכנסת במ"ש ב-[math]\displaystyle{ (-\infty,\infty)=\mathbb R }[/math].
פתרון
קל לראות ש-[math]\displaystyle{ f(x)=\lim_{n\to\infty}f_n(x)=\begin{cases}1&x=0\\0&\text{else}\end{cases} }[/math]. נבדוק התכנסות במ"ש: [math]\displaystyle{ \sup_{x\in\mathbb R}|f_n(x)-f(x)|\ge\sup_{x\in\mathbb R}|f_n(x)|=\left|\sup_{x\in\mathbb R}\frac1{1+n^2x^2}\right|=\left|\sup_{x\in[0,\infty)}\frac1{1+n^2x^2}\right| }[/math]. נחפש מקסימום: [math]\displaystyle{ f_n'(x)=\frac{-2n^2x}{\left(1+n^2x^2\right)^2}=0 }[/math] וקל לראות שהנגזרת מתאפסת עבור [math]\displaystyle{ x=0 }[/math]. ברור ש-[math]\displaystyle{ f_n }[/math] מונוטונית יורדת ב-[math]\displaystyle{ [0,\infty) }[/math] ולכן זו אכן נקודת מקסימום גלובלית. מתקיים [math]\displaystyle{ f_n(0)=1 }[/math] ולכן [math]\displaystyle{ \sup_{x\in\mathbb R}|f_n(x)-f(x)|\ge1\not\to0 }[/math]. מכאן שההתכנסות נקודתית בלבד. [math]\displaystyle{ \blacksquare }[/math]
דוגמה 3
תהי [math]\displaystyle{ \{f_n\} }[/math] סדרת פונקציות המתכנסת במ"ש לפונקציה f, האם f חסומה?
פתרון
נבחר לדוגמה [math]\displaystyle{ f_n(x)=\frac1x+\frac1n }[/math] בקטע [math]\displaystyle{ (0,\infty) }[/math]. ברור כי [math]\displaystyle{ f(x)=\lim_{n\to\infty}f_n(x)=\frac1x }[/math] וכי אם [math]\displaystyle{ x\to0^+ }[/math] אז [math]\displaystyle{ \frac1x\to\infty }[/math], לכן f לא חסומה. [math]\displaystyle{ \blacksquare }[/math]
דוגמה 4
תהי [math]\displaystyle{ \{f_n\} }[/math] סדרת פונקציות המתכנסת לפונקציה f במ"ש ב-I. נוכיח כי אם כל אחת מהפונקציות [math]\displaystyle{ f_n }[/math] חסומה ב-I, אזי גם f חסומה ב-I.
פתרון
נרשום [math]\displaystyle{ |f|\le|f-f_n|+|f_n| }[/math]. נתון כי ההתכנסות במ"ש ולכן [math]\displaystyle{ \forall\varepsilon\gt 0:\ \exists n_0:\ \forall n\gt n_0:\ |f(x)-f_n(x)|\lt \varepsilon }[/math], בפרט עבור [math]\displaystyle{ \varepsilon=1 }[/math]. כמו כן [math]\displaystyle{ f_{n_0+1} }[/math] חסומה ב-I (מהנתון) כלומר קיים M כך ש-[math]\displaystyle{ \sup_{x\in I}|f_{n_0+1}(x)|\le M\lt \infty }[/math] ולכן מתקבל ש-[math]\displaystyle{ |f(x)|\le1+|f_{n_0+1}(x)|\lt 1+M }[/math] לכל [math]\displaystyle{ x\in I }[/math]. [math]\displaystyle{ \blacksquare }[/math]
משפט: אם [math]\displaystyle{ f_n }[/math] מתכנסת במ"ש בקטע I וכל [math]\displaystyle{ f_n }[/math] רציפה אזי f רציפה.
דוגמה 5
ניתן דוגמה לסדרת פונקציות רציפות המתכנסות לפונקציה רציפה אבל לא מתכנסת במ"ש.
פתרון
נגדיר את הפונקציה הבאה: [math]\displaystyle{ f_n(x)=\begin{cases}2nx&0\le x\le\frac1{2n}\\2-2nx&\frac1{2n}\lt x\le\frac1n\\0&\frac1n\lt x\le1\end{cases} }[/math]. קל לראות שהפונקציה הנ"ל מוגדרת בקטע [math]\displaystyle{ [0,1] }[/math], אפשר לראות שהפונקציה הנ"ל רציפה.
לכל [math]\displaystyle{ x_0 }[/math] יש [math]\displaystyle{ n_0 }[/math] כך שלכל [math]\displaystyle{ n\gt n_0 }[/math] מתקיים [math]\displaystyle{ x_0\gt \frac1{n_0} }[/math] שם מתקיים [math]\displaystyle{ f_n(x_0)=0 }[/math], כלומר [math]\displaystyle{ \{f_n(x_0)\} }[/math] סדרה קבועה מ-[math]\displaystyle{ n_0 }[/math] מסויים. כמו כן [math]\displaystyle{ \sup_{x\in[0,1]}|f_n(x)-f(x)|=1 }[/math] ולכן ההתכנסות אינה במ"ש.
טורים של פונקציות
דוגמה 6
נסמן לכל n, [math]\displaystyle{ f_n(x)=x^{n-1} }[/math] בקטע [math]\displaystyle{ (-1,1) }[/math]. מה היא פונקצית הסכום [math]\displaystyle{ S_N }[/math]?
פתרון
[math]\displaystyle{ S_N(x)=\sum_{n=1}^N f_n(x)=1+x+\dots+x^{N-1}=\frac{1-x^N}{1-x}\to\frac1{1-x} }[/math].
דוגמה 7
נוכיח כי הטור [math]\displaystyle{ S_N(x)=\sum_{n=0}^N\frac{(-1)^nx^{2n+1}}{(2n+1)!} }[/math] מתכנס ל-[math]\displaystyle{ \sin(x) }[/math] במ"ש בקטע [math]\displaystyle{ [0,2\pi] }[/math] כאשר [math]\displaystyle{ n\to\infty }[/math].
פתרון
בזכות טורי טיילור ברור שיש התכנסות נקודתית, נותר לבדוק התכנסות במ"ש. נסמן [math]\displaystyle{ f_n(x)=\frac{(-1)^nx^{2n+1}}{(2n+1)!} }[/math]. כאשר [math]\displaystyle{ R_N(x) }[/math] השארית בין הטור-טיילור מסדר N לבין [math]\displaystyle{ \sin }[/math] מתקיים [math]\displaystyle{ |S_N(x)-\sin(x)|=|R_N(x)|\le\left|\frac{x^{2(N+1)+1}}{(2(N+1)+1)!}\right| }[/math]. כמו כן [math]\displaystyle{ \frac{x^{2N+3}}{(2N+3)!}\le\frac{(2\pi)^{2N+3}}{(2N+3)!}=:a_N }[/math]. נוכיח ש-[math]\displaystyle{ a_N\to0 }[/math] וכך נוכיח שההתכנסות במ"ש. מספיק להסתכל על [math]\displaystyle{ \left|\frac{a_{N+1}}{a_N}\right|=\frac{(2\pi)^{2N+5}}{(2N+5)!}\frac{(2N+3)!}{(2\pi)^{2N+3}}=\frac{(2\pi)^2}{(2N+4)(2N+5)}\to0 }[/math], לכן [math]\displaystyle{ \sum_{n=1}^\infty a_n }[/math] מתכנס ובפרט [math]\displaystyle{ a_n\to0 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
דוגמה 8
בדקו התכנסות במ"ש של [math]\displaystyle{ \sum_{n=1}^\infty \frac{\cos(nx)}{n^2} }[/math].
פתרון
נשים לב כי לא ידועה לנו פונקצית הגבול של הטור ולכן לא ניתן להוכיח התכנסות במ"ש ישירות מההגדרה. במקום, נפנה לתנאי קושי: יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. ברור כי [math]\displaystyle{ \left|\sum_{k=n}^m\frac{\cos(kx)}{k^2}\right|\le\left|\sum_{k=n}^m\frac1{k^2}\right| }[/math]. הטור [math]\displaystyle{ \sum_{k=1}^\infty\frac1{k^2} }[/math] מתכנס ולכן מקיים את תנאי קושי, כלומר קיים [math]\displaystyle{ n_0\in\mathbb N }[/math] כל שלכל [math]\displaystyle{ m\gt n\gt n_0 }[/math] מתקיים [math]\displaystyle{ \left|\sum_{k=n}^m\frac1{k^2}\right|\lt \varepsilon }[/math]. לכן, עבור אותו [math]\displaystyle{ n_0 }[/math], לכל [math]\displaystyle{ m\gt n\gt n_0 }[/math] מתקיים [math]\displaystyle{ \left|\sum_{k=n}^m\frac{\cos(kx)}{k^2}\right|\lt \varepsilon }[/math]. [math]\displaystyle{ \blacksquare }[/math]