משתמש:אור שחף/133 - הרצאה/29.3.11: הבדלים בין גרסאות בדף
(←שלב ג) |
מאין תקציר עריכה |
||
| שורה 1: | שורה 1: | ||
=מבוא לאינטגרציה נומרית {{הערה|(המשך)}}= | =מבוא לאינטגרציה נומרית {{הערה|(המשך)}}= | ||
<ol start="3"> | <ol start="3"> | ||
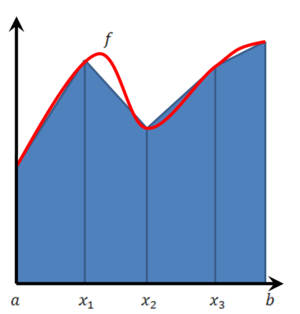
<li>שיטת הטרפזים: נעשה חלוקה שווה של <math>[a,b]</math>: <math>a=x_0<x_1<\dots<x_n=b</math>, כאשר <math>x_k-x_{k-1}=\frac{b-a}n=h</math>. חלוקת הקטע <math>[a,b]</math> משרה חלוקת הגרף <math>y=f(x)</math>. נחבר את הנקודות האלה בגרף ע"י קווים ישרים, וכך ניצור איחוד של n טרפזים (במקום מלבנים בשיטה של סכומי רימן), והשטח הכולל של הטרפזים הוא קירוב של האינטגרל. לטרפז שמעל <math>[x_{k-1},x_k]</math> יש רוחב h ושני גבהים <math>f(x_{k-1}),\ f(x_k)</math>. לכן שטח אותו טרפז הוא <math>\frac{f(x_{k-1})+f(x_k)}2h</math>, והקירוב לאינטגרל הוא {{left|<math>\begin{align}\sum_{k=1}^n \frac{f(x_{k-1})+f(x_k)}2h&=h\left(\frac{f(x_0)}2+\frac{f(x_1)}2+\dots+\frac{f(x_n)}2\right)\\&=\left(\frac{f(x_0)}2+\frac{f(x_n)}2\right)h+h\sum_{k=1}^{n-1} f(x_k)\end{align}</math>}} | <li> | ||
נותר לחשב את סדר הגודל של הטעות. נסמן לכל פונקציה g <math>I(g)=\int\limits_{x_{k-1}}^{x_k} g(x)\mathrm dx</math> וכן <math>T(g)</math> הקירוב של g ע"י טרפז. עתה נתמקד באחד הקטעים <math>[x_{k-1},x_k]</math> ונעריך את הטעות בו, השווה ל-<math>\int\limits_{x_{k-1}}^{x_k} f(x)\mathrm dx-\frac{f(x_{k-1})+f(x_k)}2h=I(f)-T(f)</math>. נשים לב כי אם f לינארית בקטע אז הטעות היא 0. | ==שיטת הטרפזים== | ||
[[קובץ:שיטת הטרפזים.png|300px|ימין]] | |||
נעשה חלוקה שווה של <math>[a,b]</math>: <math>a=x_0<x_1<\dots<x_n=b</math>, כאשר <math>x_k-x_{k-1}=\frac{b-a}n=h</math>. חלוקת הקטע <math>[a,b]</math> משרה חלוקת הגרף <math>y=f(x)</math>. נחבר את הנקודות האלה בגרף ע"י קווים ישרים, וכך ניצור איחוד של n טרפזים (במקום מלבנים בשיטה של סכומי רימן), והשטח הכולל של הטרפזים הוא קירוב של האינטגרל. לטרפז שמעל <math>[x_{k-1},x_k]</math> יש רוחב h ושני גבהים <math>f(x_{k-1}),\ f(x_k)</math>. לכן שטח אותו טרפז הוא <math>\frac{f(x_{k-1})+f(x_k)}2h</math>, והקירוב לאינטגרל הוא {{left|<math>\begin{align}\sum_{k=1}^n \frac{f(x_{k-1})+f(x_k)}2h&=h\left(\frac{f(x_0)}2+2\frac{f(x_1)}2+2\frac{f(x_2)}2+\dots+\frac{f(x_n)}2\right)\\&=\left(\frac{f(x_0)}2+\frac{f(x_n)}2\right)h+h\sum_{k=1}^{n-1} f(x_k)\end{align}</math>}} | |||
נותר לחשב את סדר הגודל של הטעות. נסמן לכל פונקציה g <math>I(g)=\int\limits_{x_{k-1}}^{x_k} g(x)\mathrm dx</math> וכן <math>T(g)</math> הקירוב של <math>I(g)</math> ע"י טרפז. עתה נתמקד באחד הקטעים <math>[x_{k-1},x_k]</math> ונעריך את הטעות בו, השווה ל-<math>\int\limits_{x_{k-1}}^{x_k} f(x)\mathrm dx-\frac{f(x_{k-1})+f(x_k)}2h=I(f)-T(f)</math>. נשים לב כי אם f לינארית בקטע אז הטעות היא 0. | |||
כעת נניח ש-f בעלת שתי נגזרות רציפות ב-<math>[a,b]</math> ונסמן <math>M=\max_{x\in[a,b]} |f''(x)|</math>. נפתח את f לפיתוח טיילור סביב הנקודה <math>x_{k-1}</math>: <math>f(x)=\underbrace{f(x_{k-1})+f'(x_{k-1})(x-x_{k-1})}_{P(x)}+\underbrace{\frac{f''(c)}2 (x-x_{k-1})^2}_{R(x)}</math>, כאשר P הוא הפיתוח הלינארי של f ו-R השארית ממנו. | כעת נניח ש-f בעלת שתי נגזרות רציפות ב-<math>[a,b]</math> ונסמן <math>M=\max_{x\in[a,b]} |f''(x)|</math>. נפתח את f לפיתוח טיילור סביב הנקודה <math>x_{k-1}</math>: <math>f(x)=\underbrace{f(x_{k-1})+f'(x_{k-1})(x-x_{k-1})}_{P(x)}+\underbrace{\frac{f''(c)}2 (x-x_{k-1})^2}_{R(x)}</math>, כאשר P הוא הפיתוח הלינארי של f ו-R השארית ממנו. | ||
לפיכך <math>I(f)=I(P)+I(R)</math>, <math>T(f)=T(P)+T(R)</math> והשארית <math>I(f)-T(f)</math> היא <math>I(P)-T(P)+I(R)-T(R)</math>, ומכיוון ש-P לינארית <math>I(P)-T(P)=0</math>, כלומר השארית היא <math>I(R)-T(R)</math>. נחשב: {{left|<math>\begin{align}|I(R)|&=\left|\int\limits_{x_{k-1}}^{x_k} \frac{f''(c)}2 (x-x_k)^2\mathrm dx\right|\\&=\int\limits_{x_{k-1}}^{x_k} \frac{|f''(c)|}2 (x-x_k)^2\mathrm dx\\&\le\frac M2\left[\frac{(x-x_{k-1})^3}3\right]_{x=x_{x-1}}^{x_k}\\&=\frac M2\frac{(x_k-x_{k-1})^3}3\\&=\frac {Mh^3}6\end{align}</math>}} | |||
וכן {{left|<math>\begin{align}T(R)&=\frac{\frac{f''(c)}2 (x_{k}-x_{k-1})^2+\frac{f''(c)}2 h^2}2h\\&=\frac{f''(c) | וכן {{left|<math>\begin{align}|T(R)|&=\left|\frac{\frac{f''(c)}2 (x_{k-1}-x_{k-1})^2+\frac{f''(c)}2 h^2}2h\right|\\&=\left|\frac{f''(c)}4h^3\right|\\&\le\frac{Mh^3}4\end{align}</math>}} | ||
בסה"כ הטעות בקטע <math>[x_{k-1},x_k]</math> חסומה ע"י <math>\frac{Mh^3}4+\frac {Mh^3}6</math>. יש n קטעים כאלה, לכן <math>|I(f)-T(f)|\le\frac {5Mh^3}{12}n=\frac {5Mh^2}{12}(b-a)</math>. | בסה"כ הטעות בקטע <math>[x_{k-1},x_k]</math> חסומה ע"י <math>\frac{Mh^3}4+\frac {Mh^3}6</math>. יש n קטעים כאלה, לכן <math>|I(f)-T(f)|\le\frac {5Mh^3}{12}n=\frac {5Mh^2}{12}(b-a)</math>. | ||
</li><li>כלל סימפסון (Simpson's Role) | </li><li> | ||
==כלל סימפסון (Simpson's Role)== | |||
שוב נקרב את <math>\int\limits_a^b f</math> בעזרת חלוקה שווה <math>a=x_0<x_1<\dots<x_n=b,\ h=\frac{b-a}n</math>, אלא שהפעם נדרוש ש-n זוגי. הקירוב של סימפסון הוא <math>S(f)=\frac h3\left(f(x_0)+4\sum_{k=1}^{n/2}f(x_{2k-1})+2\sum_{k=1}^{n/2-1}f(x_{2k})+f(x_n)\right)</math>. למעשה, סימפסון מקרב <math>\int\limits_{x_{k-1}}^{x_{k+1}} f</math> ע"י <math>\frac | |||
h3\Big(f(x_{k-1})+4f(x_k)+f(x_{k+1})\Big)</math> | h3\Big(f(x_{k-1})+4f(x_k)+f(x_{k+1})\Big)</math> | ||
לפני ההוכחה נציג שתי למות להשכלה כללית (באינפי): | לפני ההוכחה נציג שתי למות להשכלה כללית (באינפי): | ||
<ul><li>נניח ש-f אינטגרבילית ואי-זוגית בקטע סימטרי <math>[-R,R]</math> אזי <math>\int\limits_{-R}^R f=0</math>. | <ul><li>נניח ש-f אינטגרבילית ואי-זוגית בקטע סימטרי <math>[-R,R]</math> אזי <math>\int\limits_{-R}^R f=0</math>. | ||
נסמן <math>I_1=\int\limits_{-R}^0 f\ \and\ I_2=\int\limits_0^R f</math> ולכן <math>I_1+I_2=\int\limits_{-R}^R f</math>. ב-<math>I_1</math> נציב <math>t=-x\implies \mathrm dt=-\mathrm dx</math> ונקבל <math>I_1=\int\limits_{-(-R)}^{-0} f(-t)(-\mathrm dt)=-\left(-\int\limits_0^R -f(t)\mathrm dt\right)=-I_2</math>. {{משל}}</li> | '''הוכחה:''' נסמן <math>I_1=\int\limits_{-R}^0 f\ \and\ I_2=\int\limits_0^R f</math> ולכן <math>I_1+I_2=\int\limits_{-R}^R f</math>. ב-<math>I_1</math> נציב <math>t=-x\implies \mathrm dt=-\mathrm dx</math> ונקבל <math>I_1=\int\limits_{-(-R)}^{-0} f(-t)(-\mathrm dt)=-\left(-\int\limits_0^R -f(t)\mathrm dt\right)=-I_2</math>. {{משל}}</li> | ||
<li>נניח ש-f רציפה בסביבה של <math>x_0</math> וגזירה בסביבה מנוקבת של <math>x_0</math>. עוד נניח שקיים <math>\lim_{x\to x_0}f'(x)=L</math>. אזי <math>f'(x_0)</math> קיים ושווה ל-L. | <li>נניח ש-f רציפה בסביבה של <math>x_0</math> וגזירה בסביבה מנוקבת של <math>x_0</math>. עוד נניח שקיים <math>\lim_{x\to x_0}f'(x)=L</math>. אזי <math>f'(x_0)</math> קיים ושווה ל-L. | ||
לפי ההגדרה, אם f גזירה ב-<math>x_0</math> אזי <math>f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}</math>, ולפי משפט לגראנז' זה שווה ל-<math>\lim_{x\to x_0} f'(c)</math> עבור <math>c</math> כלשהו בין <math>x</math> ל-<math>x_0</math>. לכן, כאשר <math>x\to x_0</math> גם <math>c\to x_0</math> ונקבל <math>L=\lim_{c\to x_0} f'(c)=\lim_{x\to x_0} f'(c)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0)</math>. {{משל}} | '''הוכחה:''' לפי ההגדרה, אם f גזירה ב-<math>x_0</math> אזי <math>f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}</math>, ולפי משפט לגראנז' זה שווה ל-<math>\lim_{x\to x_0} f'(c)</math> עבור <math>c</math> כלשהו בין <math>x</math> ל-<math>x_0</math>. לכן, כאשר <math>x\to x_0</math> גם <math>c\to x_0</math> ונקבל <math>L=\lim_{c\to x_0} f'(c)=\lim_{x\to x_0} f'(c)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0)</math>. {{משל}} | ||
</li></ul> | </li></ul> | ||
נחזור לכלל סימפסון. | נחזור לכלל סימפסון. | ||
==שלב א== | ===שלב א=== | ||
נניח ש-<math>h>0</math> ו-<math>p(x)</math> פולינום ממעלה 3 או פחות. נוכיח ש-<math>\int\limits_{-h}^h p=\frac h3\Big(p(-h)+4p(0)+p(h)\Big)\implies I(p)=S(p)</math> (כאשר לכל f אינטגרבילית ב-<math>[-h,h]</math> הגדרנו <math>I(f)=\int\limits_{-h}^h f</math>). | נניח ש-<math>h>0</math> ו-<math>p(x)</math> פולינום ממעלה 3 או פחות. נוכיח ש-<math>\int\limits_{-h}^h p=\frac h3\Big(p(-h)+4p(0)+p(h)\Big)\implies I(p)=S(p)</math> (כאשר לכל f אינטגרבילית ב-<math>[-h,h]</math> הגדרנו <math>I(f)=\int\limits_{-h}^h f</math>). | ||
===הוכחה=== | ====הוכחה==== | ||
לכל פולינום ממעלה 3 (או פחות) <math>p(x)=\sum_{k=0}^3 \alpha_kx^k</math> מתקיים {{left|<math>\begin{align}I(p)&=\sum_{k=0}^3 \int\limits_{-h}^h \alpha_kx^k\mathrm dx\\&=\sum_{k=0}^3 \left[\alpha_k\frac{x^{k+1}}{k+1}\right]_{x=-h}^h\\&=2h\alpha_0+0+\frac23h^3\alpha_2+0\\&=\frac h3\left(6\alpha_0+2h^2\alpha_2\right)\\&=\frac h3\Big(\left(\alpha_0-h\alpha_1+h^2\alpha_2-h^3\alpha_3\right)+4\alpha_0+\left(\alpha_0+h\alpha_1+h^2\alpha_2+h^3\alpha_3\right)\Big)\\&=S(p)\end{align}</math>}} | לכל פולינום ממעלה 3 (או פחות) <math>p(x)=\sum_{k=0}^3 \alpha_kx^k</math> מתקיים {{left|<math>\begin{align}I(p)&=\sum_{k=0}^3 \int\limits_{-h}^h \alpha_kx^k\mathrm dx\\&=\sum_{k=0}^3 \left[\alpha_k\frac{x^{k+1}}{k+1}\right]_{x=-h}^h\\&=2h\alpha_0+0+\frac23h^3\alpha_2+0\\&=\frac h3\left(6\alpha_0+2h^2\alpha_2\right)\\&=\frac h3\Big(\left(\alpha_0-h\alpha_1+h^2\alpha_2-h^3\alpha_3\right)+4\alpha_0+\left(\alpha_0+h\alpha_1+h^2\alpha_2+h^3\alpha_3\right)\Big)\\&=S(p)\end{align}</math>}} | ||
==שלב ב== | ===שלב ב=== | ||
נניח ש-f בעלת 4 נגזרות רציפות בקטע <math>[-h,h]</math> ונסמן <math>M=\max_{x\in[-h,h]}\left|f^{(4)}(x)\right|</math>. נעריך את הטעות: <math>\int\limits_{-h}^h f-\frac h3\Big(f(-h)+4f(0)+f(h)\Big)=I(f)-S(f)</math>. לצורך זה נשתמש בפיתוח טיילור של f סביב 0 מסדר 3, <math>f(x)=P_3(x)+R_3(x)</math>. לכן <math>I(f)-S(f)=\underbrace{I(P_3)-S(P_3)}_0+I(R_3)-S(R_3)</math>. כזכור <math>R_3(x)=\frac{f^{(4)}(c)x^4}{4!}</math>. נעריך: {{left|<math>\begin{align}|I(R_3)|&=\left|\int\limits_{-h}^h\frac{f^{(4)}(c)x^4}{4!}\mathrm dx\right|\\&\le\frac M{4!}\int\limits_{-h}^h\left|x^4\right|\mathrm dx\\&=\frac M{24}\left[\frac{x^5}5\right]_{x=-h}^h\\&=\frac{Mh^5}{60}\end{align}</math>}} | נניח ש-f בעלת 4 נגזרות רציפות בקטע <math>[-h,h]</math> ונסמן <math>M=\max_{x\in[-h,h]}\left|f^{(4)}(x)\right|</math>. נעריך את הטעות: <math>\int\limits_{-h}^h f-\frac h3\Big(f(-h)+4f(0)+f(h)\Big)=I(f)-S(f)</math>. לצורך זה נשתמש בפיתוח טיילור של f סביב 0 מסדר 3, <math>f(x)=P_3(x)+R_3(x)</math>. לכן <math>I(f)-S(f)=\underbrace{I(P_3)-S(P_3)}_0+I(R_3)-S(R_3)</math>. כזכור <math>R_3(x)=\frac{f^{(4)}(c)x^4}{4!}</math>. נעריך: {{left|<math>\begin{align}|I(R_3)|&=\left|\int\limits_{-h}^h\frac{f^{(4)}(c)x^4}{4!}\mathrm dx\right|\\&\le\frac M{4!}\int\limits_{-h}^h\left|x^4\right|\mathrm dx\\&=\frac M{24}\left[\frac{x^5}5\right]_{x=-h}^h\\&=\frac{Mh^5}{60}\end{align}</math>}} | ||
{{left|<math>\begin{align}|S(R_3)|&=\left|\frac h3(R_3(-h)+4R_3(0)+R_3(h))\right|\\&=\frac h3\left|\frac{f^{(4)}(c_1)}{4!}h^4+\frac{f^{(4)}(c_2)}{4!}h^4\right|\\&\le\frac M{36}\cdot h^5\end{align}</math>}} | {{left|<math>\begin{align}|S(R_3)|&=\left|\frac h3\Big(R_3(-h)+4R_3(0)+R_3(h)\Big)\right|\\&=\frac h3\left|\frac{f^{(4)}(c_1)}{4!}h^4+\frac{f^{(4)}(c_2)}{4!}h^4\right|\\&\le\frac M{36}\cdot h^5\end{align}</math>}} | ||
מכל זה, יוצא ש: <math>|I(f)-S(f)|=|I(R_3)-S(R_3)|\le\frac M{36}h^5+\frac M{60}h^5=\frac 2{45}Mh^5</math>. | מכל זה, יוצא ש: <math>|I(f)-S(f)|=|I(R_3)-S(R_3)|\le\frac M{36}h^5+\frac M{60}h^5=\frac 2{45}Mh^5</math>. | ||
==שלב ג== | ===שלב ג=== | ||
נוכיח כי לכל k שעבורו <math>1\le k\le n-1</math> מתקיים <math>\int\limits_{x_{k-1}}^{x_k} f-\frac | נוכיח כי לכל k שעבורו <math>1\le k\le n-1</math> מתקיים <math>\int\limits_{x_{k-1}}^{x_k} f-\frac h3\left(f(x_{k-1})+4f(x_k)+f(x_{k+1})\right)=I(f)-S(f)</math> | ||
===הוכחה=== | ====הוכחה==== | ||
באינטגרל <math>I(f)</math> נציב <math>t=x-x_k</math> כדי לקבל <math>I(f)=\int\limits_{x_{k-1}-x_k}^{x_{k+1}-x_k}f(t+x_k)\mathrm dt=\int\limits_{-h}^h f(t+x_k)\mathrm dt</math>. ניצור פונקציה <math>g:t\mapsto f(t+x_k)</math> ונבנה <math>S(g)</math> ב-<math>[-h,h]</math> כמו שעשינו בשלב ב: {{left|<math>\begin{align}S(g)&=\frac h3\Big(g(-h)+4g(0)+g(h)\Big)\\&=\frac h3\Big(f(x_k-h)+4f(x_k)+f(x_k+h)\Big)\\&=\frac h3\Big(f(x_{k-1})+4f(x_k)+f(x_{k+1})\Big)\\&=S(f)\end{align}</math>}} | באינטגרל <math>I(f)</math> נציב <math>t=x-x_k</math> כדי לקבל <math>I(f)=\int\limits_{x_{k-1}-x_k}^{x_{k+1}-x_k}f(t+x_k)\mathrm dt=\int\limits_{-h}^h f(t+x_k)\mathrm dt</math>. ניצור פונקציה <math>g:t\mapsto f(t+x_k)</math> ונבנה <math>S(g)</math> ב-<math>[-h,h]</math> כמו שעשינו בשלב ב: {{left|<math>\begin{align}S(g)&=\frac h3\Big(g(-h)+4g(0)+g(h)\Big)\\&=\frac h3\Big(f(x_k-h)+4f(x_k)+f(x_k+h)\Big)\\&=\frac h3\Big(f(x_{k-1})+4f(x_k)+f(x_{k+1})\Big)\\&=S(f)\end{align}</math>}} | ||
כמו כן, מכיוון ש-<math>g(x)=f(x+x_k)</math> מתקיים <math>M=\max_{x\in[-h,h]}\left|g^{(4)}(x)\right|=\max_{x\in[x_{k-1},x_{k+1}]}\left|f^{(4)}(x)\right|</math>, ומכל זה נובע <math>I_{[x_{k-1},x_{k+1}]}(f)-S_{[x_{k-1},x_{k+1}]}(f)=I_{[-h,h]}(g)-S_{[-h,h]}(g)\le\frac2{45}Mh^5</math>. | כמו כן, מכיוון ש-<math>g(x)=f(x+x_k)</math> מתקיים <math>M=\max_{x\in[-h,h]}\left|g^{(4)}(x)\right|=\max_{x\in[x_{k-1},x_{k+1}]}\left|f^{(4)}(x)\right|</math>, ומכל זה נובע <math>I_{[x_{k-1},x_{k+1}]}(f)-S_{[x_{k-1},x_{k+1}]}(f)=I_{[-h,h]}(g)-S_{[-h,h]}(g)\le\frac2{45}Mh^5</math>. | ||
==סיכום== | ===סיכום=== | ||
מצאנו שעל כל תת קטע <math>[x_{k-1},x_{k+1}]</math> הטעות בקירוב סימפסון חסומה ע"י <math>\frac2{45}Mh^5</math>. יש <math>\frac n2</math> קטעים כאלה, ומכיוון ש-<math>h=\frac{b-a}n\implies n=\frac{b-a}h</math> הטעות חסומה ע"י <math>\frac2{45}Mh^5\frac{b-a}{2h}=\frac{Mh^4(b-a)}{45}</math>. | מצאנו שעל כל תת קטע <math>[x_{k-1},x_{k+1}]</math> הטעות בקירוב סימפסון חסומה ע"י <math>\frac2{45}Mh^5</math>. יש <math>\frac n2</math> קטעים כאלה, ומכיוון ש-<math>h=\frac{b-a}n\implies n=\frac{b-a}h</math> הטעות חסומה ע"י <math>\frac2{45}Mh^5\frac{b-a}{2h}=\frac{Mh^4(b-a)}{45}</math>. | ||
גרסה אחרונה מ־16:40, 25 ביולי 2011
מבוא לאינטגרציה נומרית (המשך)
-
שיטת הטרפזים
נעשה חלוקה שווה של [math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math], כאשר [math]\displaystyle{ x_k-x_{k-1}=\frac{b-a}n=h }[/math]. חלוקת הקטע [math]\displaystyle{ [a,b] }[/math] משרה חלוקת הגרף [math]\displaystyle{ y=f(x) }[/math]. נחבר את הנקודות האלה בגרף ע"י קווים ישרים, וכך ניצור איחוד של n טרפזים (במקום מלבנים בשיטה של סכומי רימן), והשטח הכולל של הטרפזים הוא קירוב של האינטגרל. לטרפז שמעל [math]\displaystyle{ [x_{k-1},x_k] }[/math] יש רוחב h ושני גבהים [math]\displaystyle{ f(x_{k-1}),\ f(x_k) }[/math]. לכן שטח אותו טרפז הוא [math]\displaystyle{ \frac{f(x_{k-1})+f(x_k)}2h }[/math], והקירוב לאינטגרל הוא[math]\displaystyle{ \begin{align}\sum_{k=1}^n \frac{f(x_{k-1})+f(x_k)}2h&=h\left(\frac{f(x_0)}2+2\frac{f(x_1)}2+2\frac{f(x_2)}2+\dots+\frac{f(x_n)}2\right)\\&=\left(\frac{f(x_0)}2+\frac{f(x_n)}2\right)h+h\sum_{k=1}^{n-1} f(x_k)\end{align} }[/math]נותר לחשב את סדר הגודל של הטעות. נסמן לכל פונקציה g [math]\displaystyle{ I(g)=\int\limits_{x_{k-1}}^{x_k} g(x)\mathrm dx }[/math] וכן [math]\displaystyle{ T(g) }[/math] הקירוב של [math]\displaystyle{ I(g) }[/math] ע"י טרפז. עתה נתמקד באחד הקטעים [math]\displaystyle{ [x_{k-1},x_k] }[/math] ונעריך את הטעות בו, השווה ל-[math]\displaystyle{ \int\limits_{x_{k-1}}^{x_k} f(x)\mathrm dx-\frac{f(x_{k-1})+f(x_k)}2h=I(f)-T(f) }[/math]. נשים לב כי אם f לינארית בקטע אז הטעות היא 0.
כעת נניח ש-f בעלת שתי נגזרות רציפות ב-[math]\displaystyle{ [a,b] }[/math] ונסמן [math]\displaystyle{ M=\max_{x\in[a,b]} |f''(x)| }[/math]. נפתח את f לפיתוח טיילור סביב הנקודה [math]\displaystyle{ x_{k-1} }[/math]: [math]\displaystyle{ f(x)=\underbrace{f(x_{k-1})+f'(x_{k-1})(x-x_{k-1})}_{P(x)}+\underbrace{\frac{f''(c)}2 (x-x_{k-1})^2}_{R(x)} }[/math], כאשר P הוא הפיתוח הלינארי של f ו-R השארית ממנו.
לפיכך [math]\displaystyle{ I(f)=I(P)+I(R) }[/math], [math]\displaystyle{ T(f)=T(P)+T(R) }[/math] והשארית [math]\displaystyle{ I(f)-T(f) }[/math] היא [math]\displaystyle{ I(P)-T(P)+I(R)-T(R) }[/math], ומכיוון ש-P לינארית [math]\displaystyle{ I(P)-T(P)=0 }[/math], כלומר השארית היא [math]\displaystyle{ I(R)-T(R) }[/math]. נחשב:[math]\displaystyle{ \begin{align}|I(R)|&=\left|\int\limits_{x_{k-1}}^{x_k} \frac{f''(c)}2 (x-x_k)^2\mathrm dx\right|\\&=\int\limits_{x_{k-1}}^{x_k} \frac{|f''(c)|}2 (x-x_k)^2\mathrm dx\\&\le\frac M2\left[\frac{(x-x_{k-1})^3}3\right]_{x=x_{x-1}}^{x_k}\\&=\frac M2\frac{(x_k-x_{k-1})^3}3\\&=\frac {Mh^3}6\end{align} }[/math]וכן[math]\displaystyle{ \begin{align}|T(R)|&=\left|\frac{\frac{f''(c)}2 (x_{k-1}-x_{k-1})^2+\frac{f''(c)}2 h^2}2h\right|\\&=\left|\frac{f''(c)}4h^3\right|\\&\le\frac{Mh^3}4\end{align} }[/math]בסה"כ הטעות בקטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] חסומה ע"י [math]\displaystyle{ \frac{Mh^3}4+\frac {Mh^3}6 }[/math]. יש n קטעים כאלה, לכן [math]\displaystyle{ |I(f)-T(f)|\le\frac {5Mh^3}{12}n=\frac {5Mh^2}{12}(b-a) }[/math].
-
כלל סימפסון (Simpson's Role)
שוב נקרב את [math]\displaystyle{ \int\limits_a^b f }[/math] בעזרת חלוקה שווה [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b,\ h=\frac{b-a}n }[/math], אלא שהפעם נדרוש ש-n זוגי. הקירוב של סימפסון הוא [math]\displaystyle{ S(f)=\frac h3\left(f(x_0)+4\sum_{k=1}^{n/2}f(x_{2k-1})+2\sum_{k=1}^{n/2-1}f(x_{2k})+f(x_n)\right) }[/math]. למעשה, סימפסון מקרב [math]\displaystyle{ \int\limits_{x_{k-1}}^{x_{k+1}} f }[/math] ע"י [math]\displaystyle{ \frac h3\Big(f(x_{k-1})+4f(x_k)+f(x_{k+1})\Big) }[/math]
לפני ההוכחה נציג שתי למות להשכלה כללית (באינפי):
- נניח ש-f אינטגרבילית ואי-זוגית בקטע סימטרי [math]\displaystyle{ [-R,R] }[/math] אזי [math]\displaystyle{ \int\limits_{-R}^R f=0 }[/math]. הוכחה: נסמן [math]\displaystyle{ I_1=\int\limits_{-R}^0 f\ \and\ I_2=\int\limits_0^R f }[/math] ולכן [math]\displaystyle{ I_1+I_2=\int\limits_{-R}^R f }[/math]. ב-[math]\displaystyle{ I_1 }[/math] נציב [math]\displaystyle{ t=-x\implies \mathrm dt=-\mathrm dx }[/math] ונקבל [math]\displaystyle{ I_1=\int\limits_{-(-R)}^{-0} f(-t)(-\mathrm dt)=-\left(-\int\limits_0^R -f(t)\mathrm dt\right)=-I_2 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- נניח ש-f רציפה בסביבה של [math]\displaystyle{ x_0 }[/math] וגזירה בסביבה מנוקבת של [math]\displaystyle{ x_0 }[/math]. עוד נניח שקיים [math]\displaystyle{ \lim_{x\to x_0}f'(x)=L }[/math]. אזי [math]\displaystyle{ f'(x_0) }[/math] קיים ושווה ל-L. הוכחה: לפי ההגדרה, אם f גזירה ב-[math]\displaystyle{ x_0 }[/math] אזי [math]\displaystyle{ f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0} }[/math], ולפי משפט לגראנז' זה שווה ל-[math]\displaystyle{ \lim_{x\to x_0} f'(c) }[/math] עבור [math]\displaystyle{ c }[/math] כלשהו בין [math]\displaystyle{ x }[/math] ל-[math]\displaystyle{ x_0 }[/math]. לכן, כאשר [math]\displaystyle{ x\to x_0 }[/math] גם [math]\displaystyle{ c\to x_0 }[/math] ונקבל [math]\displaystyle{ L=\lim_{c\to x_0} f'(c)=\lim_{x\to x_0} f'(c)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0) }[/math]. [math]\displaystyle{ \blacksquare }[/math]
נחזור לכלל סימפסון.
שלב א
נניח ש-[math]\displaystyle{ h\gt 0 }[/math] ו-[math]\displaystyle{ p(x) }[/math] פולינום ממעלה 3 או פחות. נוכיח ש-[math]\displaystyle{ \int\limits_{-h}^h p=\frac h3\Big(p(-h)+4p(0)+p(h)\Big)\implies I(p)=S(p) }[/math] (כאשר לכל f אינטגרבילית ב-[math]\displaystyle{ [-h,h] }[/math] הגדרנו [math]\displaystyle{ I(f)=\int\limits_{-h}^h f }[/math]).
הוכחה
לכל פולינום ממעלה 3 (או פחות) [math]\displaystyle{ p(x)=\sum_{k=0}^3 \alpha_kx^k }[/math] מתקיים[math]\displaystyle{ \begin{align}I(p)&=\sum_{k=0}^3 \int\limits_{-h}^h \alpha_kx^k\mathrm dx\\&=\sum_{k=0}^3 \left[\alpha_k\frac{x^{k+1}}{k+1}\right]_{x=-h}^h\\&=2h\alpha_0+0+\frac23h^3\alpha_2+0\\&=\frac h3\left(6\alpha_0+2h^2\alpha_2\right)\\&=\frac h3\Big(\left(\alpha_0-h\alpha_1+h^2\alpha_2-h^3\alpha_3\right)+4\alpha_0+\left(\alpha_0+h\alpha_1+h^2\alpha_2+h^3\alpha_3\right)\Big)\\&=S(p)\end{align} }[/math]שלב ב
נניח ש-f בעלת 4 נגזרות רציפות בקטע [math]\displaystyle{ [-h,h] }[/math] ונסמן [math]\displaystyle{ M=\max_{x\in[-h,h]}\left|f^{(4)}(x)\right| }[/math]. נעריך את הטעות: [math]\displaystyle{ \int\limits_{-h}^h f-\frac h3\Big(f(-h)+4f(0)+f(h)\Big)=I(f)-S(f) }[/math]. לצורך זה נשתמש בפיתוח טיילור של f סביב 0 מסדר 3, [math]\displaystyle{ f(x)=P_3(x)+R_3(x) }[/math]. לכן [math]\displaystyle{ I(f)-S(f)=\underbrace{I(P_3)-S(P_3)}_0+I(R_3)-S(R_3) }[/math]. כזכור [math]\displaystyle{ R_3(x)=\frac{f^{(4)}(c)x^4}{4!} }[/math]. נעריך:[math]\displaystyle{ \begin{align}|I(R_3)|&=\left|\int\limits_{-h}^h\frac{f^{(4)}(c)x^4}{4!}\mathrm dx\right|\\&\le\frac M{4!}\int\limits_{-h}^h\left|x^4\right|\mathrm dx\\&=\frac M{24}\left[\frac{x^5}5\right]_{x=-h}^h\\&=\frac{Mh^5}{60}\end{align} }[/math][math]\displaystyle{ \begin{align}|S(R_3)|&=\left|\frac h3\Big(R_3(-h)+4R_3(0)+R_3(h)\Big)\right|\\&=\frac h3\left|\frac{f^{(4)}(c_1)}{4!}h^4+\frac{f^{(4)}(c_2)}{4!}h^4\right|\\&\le\frac M{36}\cdot h^5\end{align} }[/math]מכל זה, יוצא ש: [math]\displaystyle{ |I(f)-S(f)|=|I(R_3)-S(R_3)|\le\frac M{36}h^5+\frac M{60}h^5=\frac 2{45}Mh^5 }[/math].
שלב ג
נוכיח כי לכל k שעבורו [math]\displaystyle{ 1\le k\le n-1 }[/math] מתקיים [math]\displaystyle{ \int\limits_{x_{k-1}}^{x_k} f-\frac h3\left(f(x_{k-1})+4f(x_k)+f(x_{k+1})\right)=I(f)-S(f) }[/math]
הוכחה
באינטגרל [math]\displaystyle{ I(f) }[/math] נציב [math]\displaystyle{ t=x-x_k }[/math] כדי לקבל [math]\displaystyle{ I(f)=\int\limits_{x_{k-1}-x_k}^{x_{k+1}-x_k}f(t+x_k)\mathrm dt=\int\limits_{-h}^h f(t+x_k)\mathrm dt }[/math]. ניצור פונקציה [math]\displaystyle{ g:t\mapsto f(t+x_k) }[/math] ונבנה [math]\displaystyle{ S(g) }[/math] ב-[math]\displaystyle{ [-h,h] }[/math] כמו שעשינו בשלב ב:[math]\displaystyle{ \begin{align}S(g)&=\frac h3\Big(g(-h)+4g(0)+g(h)\Big)\\&=\frac h3\Big(f(x_k-h)+4f(x_k)+f(x_k+h)\Big)\\&=\frac h3\Big(f(x_{k-1})+4f(x_k)+f(x_{k+1})\Big)\\&=S(f)\end{align} }[/math]כמו כן, מכיוון ש-[math]\displaystyle{ g(x)=f(x+x_k) }[/math] מתקיים [math]\displaystyle{ M=\max_{x\in[-h,h]}\left|g^{(4)}(x)\right|=\max_{x\in[x_{k-1},x_{k+1}]}\left|f^{(4)}(x)\right| }[/math], ומכל זה נובע [math]\displaystyle{ I_{[x_{k-1},x_{k+1}]}(f)-S_{[x_{k-1},x_{k+1}]}(f)=I_{[-h,h]}(g)-S_{[-h,h]}(g)\le\frac2{45}Mh^5 }[/math].
סיכום
מצאנו שעל כל תת קטע [math]\displaystyle{ [x_{k-1},x_{k+1}] }[/math] הטעות בקירוב סימפסון חסומה ע"י [math]\displaystyle{ \frac2{45}Mh^5 }[/math]. יש [math]\displaystyle{ \frac n2 }[/math] קטעים כאלה, ומכיוון ש-[math]\displaystyle{ h=\frac{b-a}n\implies n=\frac{b-a}h }[/math] הטעות חסומה ע"י [math]\displaystyle{ \frac2{45}Mh^5\frac{b-a}{2h}=\frac{Mh^4(b-a)}{45} }[/math].
הערה: ניתן להוכיח כי הטעות חסומה גם ע"י [math]\displaystyle{ \frac{Mh^4(b-a)}{180} }[/math].