88-236 אינפי 4 תשעב סמסטר ב/המחשות: הבדלים בין גרסאות בדף
אין תקציר עריכה |
אין תקציר עריכה |
||
| שורה 67: | שורה 67: | ||
[[קובץ:Gradf.jpg]] | [[קובץ:Gradf.jpg]] | ||
כפי שנאמר בכיתה, השדה הגרדיאנטי | כפי שנאמר בכיתה, השדה הגרדיאנטי מצביע תמיד בכוון העלייה התלולה ביותר בפונקציה (במקרה זה הוא מצביע הרחק מהראשית). | ||
עקומות הרמה במקרה זה הן העקומות שבהן <math>x^2+y^2=c</math> כאשר <math>c</math> קבוע. אם <math>c</math> שלילי זוהי קבוצה ריקה. אם <math>c \ge 0</math> מדובר במעגל בעל רדיוס <math>\sqrt{c}</math> שמרכזו ב-<math>(0,0)</math>. הנה אנימציה שבה חותכים את המשטח <math>z=x^2+y^2</math> עם המישור הקבוע <math>z=c</math> עבור ערכים שונים של <math>c</math> | עקומות הרמה במקרה זה הן העקומות שבהן <math>x^2+y^2=c</math> כאשר <math>c</math> קבוע. אם <math>c</math> שלילי זוהי קבוצה ריקה. אם <math>c \ge 0</math> מדובר במעגל בעל רדיוס <math>\sqrt{c}</math> שמרכזו ב-<math>(0,0)</math>. הנה אנימציה שבה חותכים את המשטח <math>z=x^2+y^2</math> עם המישור הקבוע <math>z=c</math> עבור ערכים שונים של <math>c</math> | ||
גרסה מ־16:05, 20 במרץ 2012
המחשות מתרגול 1:
בתרגול הראשון הגדרנו בקצרה ושרטטנו שדות סקלריים ווקטוריים. הנה ציורים יותר יפים שלהם (הוקטורים לא באורך המדויק, אבל מקבלים תמונה כללית):
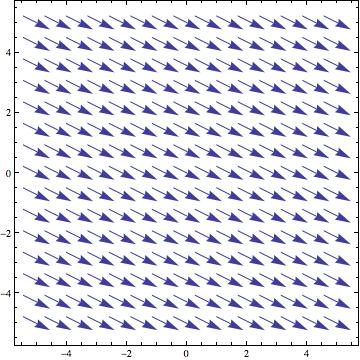
[math]\displaystyle{ \textbf{F}=(2,-1)=2 \hat{\imath}-1 \hat{\jmath} }[/math] (שדה וקטורי קבוע)
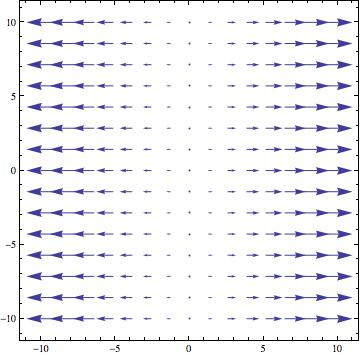
[math]\displaystyle{ \textbf{F}=(x,0)=x \hat{\imath} }[/math]
[math]\displaystyle{ \textbf{F}=(x,2y)=x \hat{\imath}+2y \hat{\jmath} }[/math]
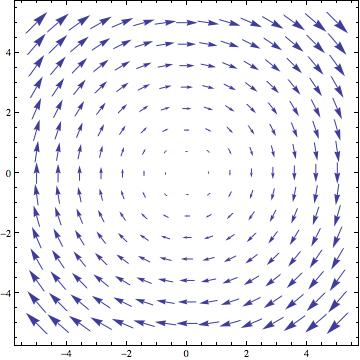
[math]\displaystyle{ \textbf{F}=(y,-x)=y \hat{\imath}-x \hat{\jmath} }[/math]
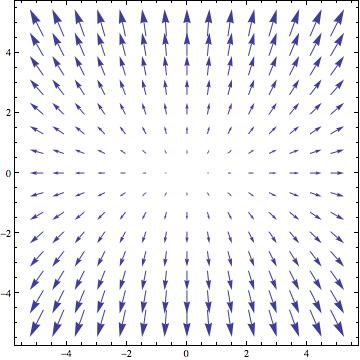
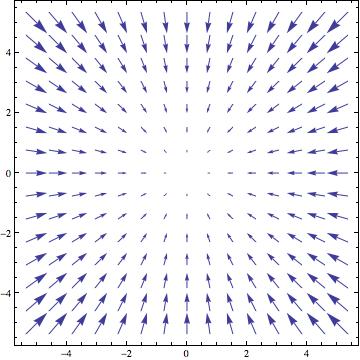
[math]\displaystyle{ \textbf{F}=(-x,-y)=-x \hat{\imath}-y \hat{\jmath} }[/math] (בכל נקודה (x,y) השדה מצביע בכוון ההפוך (x,-y-). בעקרון כל החצים צריכים להגיע לראשית אבל אז הציור יוצא פחות ברור...)
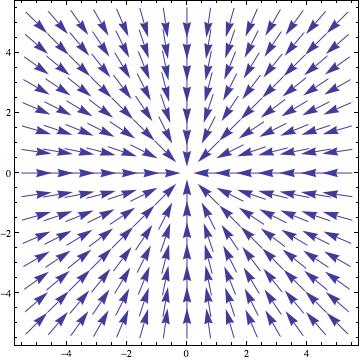
[math]\displaystyle{ \textbf{F}=\left( \frac{-x}{\sqrt{x^2+y^2}},\frac{-y}{\sqrt{x^2+y^2}} \right) }[/math]
נשים לב שזהו הנרמול של השדה הוקטורי הקודם, שכן:
[math]\displaystyle{ \| (-x,-y) \|=\sqrt{(-x)^2+(-y)^2}=\sqrt{x^2+y^2} }[/math]
כלומר, הוקטורים מצביעים באותו כיוון כמו מקודם, אבל אורכם יהיה זהה.
הערה: כפי שנאמר בתרגול, השדה הזה לא מוגדר בראשית בגלל שהמכנה מתאפס שם.
נדבר כעת על השדה הסקלרי (פונקציה סקלרית) [math]\displaystyle{ f:\mathbb{R}^2 \rightarrow \mathbb{R} }[/math] המוגדר על ידי [math]\displaystyle{ f(x,y)=x^2+y^2 }[/math]
את הגרף של [math]\displaystyle{ f }[/math] נוכל לצייר ב-[math]\displaystyle{ \mathbb{R}^3 }[/math] (מרחב [math]\displaystyle{ x,y,z }[/math]) כאשר [math]\displaystyle{ z=x^2+y^2 }[/math]
את הגרדיאנט של [math]\displaystyle{ f }[/math] אפשר לחשב בקלות:
[math]\displaystyle{ \nabla f(x,y)=(2x,2y) }[/math]
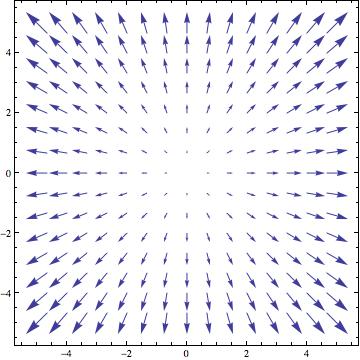
זהו שדה וקטורי, שנראה כך:
כפי שנאמר בכיתה, השדה הגרדיאנטי מצביע תמיד בכוון העלייה התלולה ביותר בפונקציה (במקרה זה הוא מצביע הרחק מהראשית).
עקומות הרמה במקרה זה הן העקומות שבהן [math]\displaystyle{ x^2+y^2=c }[/math] כאשר [math]\displaystyle{ c }[/math] קבוע. אם [math]\displaystyle{ c }[/math] שלילי זוהי קבוצה ריקה. אם [math]\displaystyle{ c \ge 0 }[/math] מדובר במעגל בעל רדיוס [math]\displaystyle{ \sqrt{c} }[/math] שמרכזו ב-[math]\displaystyle{ (0,0) }[/math]. הנה אנימציה שבה חותכים את המשטח [math]\displaystyle{ z=x^2+y^2 }[/math] עם המישור הקבוע [math]\displaystyle{ z=c }[/math] עבור ערכים שונים של [math]\displaystyle{ c }[/math]