משתמש:אור שחף/133 - הרצאה/27.2.11: הבדלים בין גרסאות בדף
מ (←הוכחה) |
|||
| (7 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 5: | שורה 5: | ||
===הוכחה=== | ===הוכחה=== | ||
<math>\ | <math>\implies</math>: נתונה f אינטגרבילית ב-<math>[a,b]</math> וב-<math>[b,c]</math>. נקח חלוקה כלשהי P של <math>[a,b]</math> וחלוקה Q של <math>[b,c]</math> ונגדיר <math>R=P\cup Q</math> (כלומר R חלוקה של <math>[a,c]</math>). לכן מתקיים <math>\overline S(f,R)=\overline S(f,P)+\overline S(f,Q)</math>. נשאיף <math>\lambda(P),\lambda(Q)\to0</math>. לפי הנתון <math>\overline S(f,P)\to\int\limits_a^b f</math> וגם <math>\overline S(f,Q)\to\int\limits_b^c f</math>, לכן <math>\overline S(f,R)\to\int\limits_a^b f+\int\limits_b^c f</math>. באותו אופן נקבל <math>\underline S(f,R)\to\int\limits_a^b f+\int\limits_b^c f</math>. הראנו ש-<math>\overline S(f,R)-\underline S(f,R)\to0</math> ולכן f אינטגרבילית ב-<math>[a,c]</math>. ע"פ משפט 4 נסיק <math>\int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f</math>. | ||
<math>\ | <math>\Longleftarrow</math>: נבחר חלוקות P,Q,R כמו בחלק הקודם, ושוב <math>\overline S(f,R)=\overline S(f,P)+\overline S(f,Q)</math> ו-<math>\underline S(f,R)=\underline S(f,P)+\underline S(f,Q)</math>. נחסיר ונקבל: <math>\overline S(f,R)-\underline S(f,R)=\overline S(f,P)-\underline S(f,P)+\overline S(f,Q)-\underline S(f,Q)</math>. כעת, אם <math>\varepsilon>0</math>, האינטגרביליות של f על <math>[a,c]</math> גוררת שעבור <math>\lambda(P)</math> ו-<math>\lambda(Q)</math> מספיק קטנים <math>\overline S(f,P)-\underline S(f,P),\overline S(f,Q)-\underline S(f,Q)<\varepsilon</math>. קיום חלוקה P כזאת לכל <math>\varepsilon>0</math> מוכיח ש-f אינטגרבילית ב-<math>[a,b]</math> וקיום חלוקה Q - ב-<math>[b,c]</math>. השיוויון <math>\int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f</math> נובע מהחלק הקודם. {{משל}} | ||
===הכללה=== | ===הכללה=== | ||
| שורה 19: | שורה 19: | ||
# <math>\int\limits_a^a f=0</math> | # <math>\int\limits_a^a f=0</math> | ||
# אם <math>a<b</math> ואם f אינטגרבילית ב-<math>[a,b]</math> נרשום <math>\int\limits_b^a f=-\int\limits_a^b f</math> | # אם <math>a<b</math> ואם f אינטגרבילית ב-<math>[a,b]</math> נרשום <math>\int\limits_b^a f=-\int\limits_a^b f</math> | ||
(אלה מוסכמות ולא | (אלה מוסכמות ולא משפטים כי באופן שבו הגדרנו את האינטגרל עד עכשיו, <math>\int\limits_b^a</math> לא מוגדר עבור <math>a\le b</math>) | ||
עם מוסכמות אלה יתקיים: | עם מוסכמות אלה יתקיים: | ||
<math>\int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f</math> באופן בלתי תלוי בסדר של המספרים a,b,c. למשל, אם <math>c<a<b</math> אז לפי משפט 8 <math>\int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f</math>. נבדוק: <math>\int\ | <math>\int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f</math> באופן בלתי תלוי בסדר של המספרים a,b,c. למשל, אם <math>c<a<b</math> אז לפי משפט 8 <math>\int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f</math>. נבדוק: <math>\int\limits_c^a f=-\int\limits_a^c f\ \and\ \int\limits_c^b f=-\int\limits_b^c f</math> ולכן <math>-\int\limits_b^c f=-\int\limits_a^c f+\int\limits_a^b f</math>, מה שגורר <math>\int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f</math>. | ||
==משפט 9== | ==משפט 9== | ||
תהי | תהי f מוגדרת וחסומה ב-<math>[a,b]</math>. עוד נניח ש-f רציפה ב-<math>(a,b]</math>. אזי f אינטגרבילית ב-<math>[a,b]</math>. | ||
===הוכחה=== | ===הוכחה=== | ||
יהי <math>\varepsilon>0</math> נתון. נגדיר <math>c=a+\frac\varepsilon{2\Omega}</math>. | יהי <math>\varepsilon>0</math> נתון. נגדיר <math>c=a+\frac\varepsilon{2\Omega}</math>. לפי הנתון f רציפה ב-<math>[c,b]</math>, אזי ממשפט 6 היא אינטגרבילית ב-<math>[c,b]</math>, לכן נוכל לבחור חלוקה P של <math>[c,b]</math> כך ש-<math>\overline S(f,P)-\underline S(f,P)<\frac\varepsilon2</math>. כעת נגדיר חלוקה Q של <math>[a,b]</math> ע"י <math>Q=\{a\}\cup P</math>. עוד נגדיר <math>M'=\sup\{f(x):\ a\le x\le c\}</math> וכן <math>m'=\inf\{f(x):\ a\le x\le c\}</math>. נובע כי {{left|<math>\begin{align}\overline S(f,Q)-\underline S(f,Q)&=(M'-m')(c-a)+\overline S(f,P)-\underline S(f,P)\\&<\Omega(c-a)+\frac\varepsilon2\\&=\Omega\cdot\frac\varepsilon{2\Omega}+\frac\varepsilon2\\&=\varepsilon\end{align}</math>}}נובע ממשפט 4 ש-f אינטגרבילית ב-<math>[a,b]</math>. {{משל}} | ||
לפי הנתון f רציפה ב-<math>[c,b]</math> | |||
===מסקנה 1=== | ===מסקנה 1=== | ||
| שורה 38: | שורה 34: | ||
===מסקנה 2=== | ===מסקנה 2=== | ||
נניח ש-f חסומה ב-<math>[a,b]</math> ורציפה שם פרט למספר סופי של נקודות <math>x_0,x_1,\dots,x_n</math> כך ש-<math>a\le x_0<x_1<\dots<x_n\le b</math> אזי f אינטגרבילית ב-<math>[a,b]</math>. | נניח ש-f חסומה ב-<math>[a,b]</math> ורציפה שם פרט למספר סופי של נקודות <math>x_0,x_1,\dots,x_n</math> כך ש-<math>a\le x_0<x_1<\dots<x_n\le b</math>. אזי f אינטגרבילית ב-<math>[a,b]</math>. | ||
====הוכחה==== | ====הוכחה==== | ||
עבור כל k נקבל ש-f חסומה ב-<math>[x_{k-1},x_k]</math> ורציפה ב-<math>(x_{k-1},x_k)</math>. לפי מסקנה 1, f אינטגרבילית ב-<math>[x_{k-1},x_k]</math>. נסתמך על | עבור כל k נקבל ש-f חסומה ב-<math>[x_{k-1},x_k]</math> ורציפה ב-<math>(x_{k-1},x_k)</math>. לפי מסקנה 1, f אינטגרבילית ב-<math>[x_{k-1},x_k]</math>. נסתמך על ההכללה למשפט 8 לומר ש-f אינטגרבילית ב-<math>[a,b]=\bigcup_{k=1}^n [x_{k-1},x_k]</math>. {{משל}} | ||
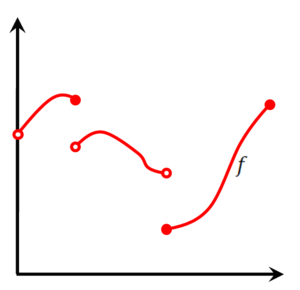
[[קובץ:פונקציה רציפה למקוטעין.png|ימין|ממוזער|300px|דוגמה לפונקציה רציפה למקוטעין]] | |||
'''הגדרה:''' אומרים ש-f "רציפה למקוטעין" ב-<math>[a,b]</math> אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון. | '''הגדרה:''' אומרים ש-f "רציפה למקוטעין" ב-<math>[a,b]</math> אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון. | ||
נובע ממסקנה 2 שכל פונקציה רציפה למקוטעין ב-<math>[a,b]</math> אינטגרבילית שם. באופן דומה אפשר להוכיח שאם f מוגדרת ו"מונוטונית למקוטעין" ב-<math>[a,b]</math> אז היא אינטגרבילית שם. | נובע ממסקנה 2 שכל פונקציה רציפה למקוטעין ב-<math>[a,b]</math> אינטגרבילית שם. באופן דומה אפשר להוכיח שאם f מוגדרת ו"מונוטונית למקוטעין" ב-<math>[a,b]</math> אז היא אינטגרבילית שם. | ||
| שורה 54: | שורה 49: | ||
=האינטגרל לפי רימן= | =האינטגרל לפי רימן= | ||
==הקדמה - הגישה של רימן== | ==הקדמה - הגישה של רימן== | ||
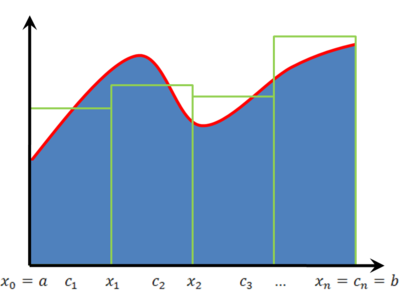
נניח ש-f מוגדרת וחסומה ב-<math>[a,b]</math>. נבחר חלוקה P של <math>[a,b]</math>: <math>a=x_0<x_1<\dots<x_n=b</math>. עוד נבחר | [[קובץ:האינטגרל לפי רימן.png|שמאל|400px|ממוזער|ניתן לראות שסכום שטחי המלבנים הנוצרים מסכום רימן שווה בקירוב לשטח שמתחת לגרף.]] | ||
נניח ש-f מוגדרת וחסומה ב-<math>[a,b]</math>. נבחר חלוקה P של <math>[a,b]</math>: <math>a=x_0<x_1<\dots<x_n=b</math>. עוד נבחר לכל k מספר <math>c_k\in[x_{k-1},x_k]</math> ונכנה כ-{{ltr|P'}} את התת חלוקה <math>a\le c_1<c_2<\dots<c_n\le b</math>. ז"א <math>a=x_0\le c_1\le x_1\le c_2\le\dots\le c_n\le x_n=b</math>. בהתאם לכך נבנה סכום רימן <math>S(f,P,P')=\sum_{k=1}^n f(c_k)\Delta x_k</math> כאשר לכל k מתקיים <math>\Delta x_k=x_k-x_{k-1}</math>. | |||
<math>S(f,P,P')</math> מקרב את השטח שמתחת לגרף, | <math>S(f,P,P')</math> מקרב את השטח שמתחת לגרף, אך לא ידוע אם הוא גדול, קטן או שווה לו. | ||
נעיר שעל חלוקה אחת P של <math>[a,b]</math> אפשר לבנות אינסוף סכומי רימן <math>S(f,P,P')</math>. עם זאת, יתקיים תמיד <math>\underline S(f,P)\le S(f,P,P')\le\overline S(f,P)</math>. יתר על כן, <math>\underline S(f,P)=\inf_{P'} S(f,P,P')</math> ו-<math>\overline S(f,P)=\sup_{P'} S(f,P,P')</math>. | נעיר שעל חלוקה אחת P של <math>[a,b]</math> אפשר לבנות אינסוף סכומי רימן <math>S(f,P,P')</math>. עם זאת, יתקיים תמיד <math>\underline S(f,P)\le S(f,P,P')\le\overline S(f,P)</math>. יתר על כן, <math>\underline S(f,P)=\inf_{P'} S(f,P,P')</math> ו-<math>\overline S(f,P)=\sup_{P'} S(f,P,P')</math>. | ||
'''הגדרת רימן:''' תהי f מוגדרת וחסומה ב-<math>[a,b]</math>. נאמר ש-f אינטגרבילית ב-<math>[a,b]</math> אם כאשר <math>\lambda(P)\to0</math> כל סכומי רימן <math>S(f,P,P')</math> שואפים לגבול אחד, שיסומן <math>\int\limits_a^b f</math>. | '''הגדרת האינטגרל לפי רימן:''' תהי f מוגדרת וחסומה ב-<math>[a,b]</math>. נאמר ש-f אינטגרבילית ב-<math>[a,b]</math> אם כאשר <math>\lambda(P)\to0</math> כל סכומי רימן <math>S(f,P,P')</math> שואפים לגבול אחד, שיסומן <math>\int\limits_a^b f</math>. | ||
==משפט 10== | ==משפט 10== | ||
| שורה 69: | שורה 63: | ||
===הוכחה=== | ===הוכחה=== | ||
תחילה נניח ש-f אינטגרבילית לפי דרבו. נעיר שלכל חלוקה P ותת חלוקה P' של <math>[a,b]</math>: | תחילה נניח ש-f אינטגרבילית לפי דרבו. נעיר שלכל חלוקה P ותת חלוקה {{ltr|P'}} של <math>[a,b]</math>: | ||
<math>\underline S(f,P)\le S(f,P,P')\le\overline S(f,P)</math>. כעת נשאיף <math>\lambda(P)\to0</math>. כיוון ש-f אינטגרבילית דרבו, <math>\overline S(f,P)\to{\int\limits_D}_a^b f</math> וכן <math>\underline S(f,P)\to{\int\limits_D}_a^b f</math> לכן משפט הסנדויץ' מבטיח ש-<math>\lim_{\lambda(P)\to0} S(f,P,P')</math> קיים ושווה ל-<math>{\int\limits_D}_a^b f</math>. ז"א f אינטגרבילית רימן ומתקיים <math>{\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P')={\int\limits_D}_a^b f</math>. | <math>\underline S(f,P)\le S(f,P,P')\le\overline S(f,P)</math>. כעת נשאיף <math>\lambda(P)\to0</math>. כיוון ש-f אינטגרבילית דרבו, <math>\overline S(f,P)\to{\int\limits_D}_a^b f</math> וכן <math>\underline S(f,P)\to{\int\limits_D}_a^b f</math> לכן משפט הסנדויץ' מבטיח ש-<math>\lim_{\lambda(P)\to0} S(f,P,P')</math> קיים ושווה ל-<math>{\int\limits_D}_a^b f</math>. ז"א f אינטגרבילית רימן ומתקיים <math>{\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P')={\int\limits_D}_a^b f</math>. | ||
לצד השני, נניח ש-f אינטגרבילית רימן. אזי מתקיים <math>{\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P')</math>. אם כן הוא גם שווה ל-<math>\lim_{\lambda(P)\to0} \sup_{P'} S(f,P,P')=\lim_{\lambda(P)\to0} \overline S(f,P)=\overline{\int}_a^b f</math>,ובאופן דומה עבור אינטגרל תחתון (לפי דרבו, כמובן). מצאנו <math>{\int\limits_R}_a^b f=\overline{\int}_a^b f=\underline\int_a^b f</math>. עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם | לצד השני, נניח ש-f אינטגרבילית רימן. אזי מתקיים <math>{\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P')</math>. אם כן הוא גם שווה ל-<math>\lim_{\lambda(P)\to0} \sup_{P'} S(f,P,P')=\lim_{\lambda(P)\to0} \overline S(f,P)=\overline{\int}_a^b f</math>,ובאופן דומה עבור אינטגרל תחתון (לפי דרבו, כמובן). מצאנו <math>{\int\limits_R}_a^b f=\overline{\int}_a^b f=\underline\int_a^b f</math>. עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם הוכחנו ש-<math>{\int\limits_R}_a^b f={\int\limits_D}_a^b f</math>. {{משל}} | ||
==משפט 11 {{הערה|(תכונות האינטגרל)}}== | ==משפט 11 {{הערה|(תכונות האינטגרל)}}== | ||
נניח ש-f ו-g מוגדרות ואינטגרביליות ב-[a,b], ונניח ש-c קבוע כלשהו. אזי: | נניח ש-f ו-g מוגדרות ואינטגרביליות ב-<math>[a,b]</math>, ונניח ש-c קבוע כלשהו. אזי: | ||
# {{הערה|(לינאריות):}} <math>f+cg</math> אינטגרבילית ב-[a,b] ומתקיים <math>\int\limits_a^ | # {{הערה|(לינאריות):}} <math>f+cg</math> אינטגרבילית ב-<math>[a,b]</math> ומתקיים <math>\int\limits_a^b(f+cg)=\int\limits_a^b f+c\int\limits_a^b g</math>. | ||
# {{הערה|(מונוטוניות):}} אם <math>f(x)\ge g(x)</math> לכל <math>x\in[a,b]</math> אז <math> | # {{הערה|(מונוטוניות):}} אם <math>f(x)\ge g(x)</math> לכל <math>x\in[a,b]</math> אז <math> | ||
\int\limits_a^b f\ge\int\limits_a^b g</math>. {{הערה|(חיוביות):}} בפרט, אם <math>\forall x\in[a,b]:\ f(x)\ge0</math> אז <math>\int\limits_a^b f\ge0</math>. | \int\limits_a^b f\ge\int\limits_a^b g</math>. {{הערה|(חיוביות):}} בפרט, אם <math>\forall x\in[a,b]:\ f(x)\ge0</math> אז <math>\int\limits_a^b f\ge0</math>. | ||
# {{הערה|( | # {{הערה|(הכללה לאי-שיוויון המשולש):}} |f| אינטגרבילית ב-<math>[a,b]</math> וגם <math>\left|\int\limits_a^b f\right|\le\int\limits_a^b |f|</math>. | ||
# אם <math>m\le f(x)\le M</math> ב-<math>[a,b]</math> אז <math>m(b-a)\le\int\limits_a^b f\le M(b-a)</math> ואם <math>|f(x)|\le M</math> בקטע זה אז אז <math>\left|\int\limits_a^b f\right|\le M(b-a)</math>. | # אם <math>m\le f(x)\le M</math> ב-<math>[a,b]</math> אז <math>m(b-a)\le\int\limits_a^b f\le M(b-a)</math> ואם <math>|f(x)|\le M</math> בקטע זה אז אז <math>\left|\int\limits_a^b f\right|\le M(b-a)</math>. | ||
# אם <math>f(x)=M</math> (פונקציה קבועה) אז <math>\int\limits_a^b f= M(b-a)</math>. | # אם <math>f(x)=M</math> (פונקציה קבועה) אז <math>\int\limits_a^b f= M(b-a)</math>. | ||
| שורה 86: | שורה 80: | ||
#<math>S(f+cg,P,P')=\sum_{k=1}^n (f+cg)(c_k)\Delta x_k=\sum_{k=1}^n f(c_k)\Delta x_k+c\sum_{k=1}^n g(c_k)\Delta x_k</math>. נשאיף <math>\lambda(P)\to0</math>. כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א <math>\lim_{\lambda(P)\to0} S(f+cg,P,P')=\int\limits_a^b f+c\int\limits_a^b g</math>. עצם קיום הגבול אומר ש-<math>f+cg</math> אינטגרבילית ולפי ערך הגבול נסיק <math>\int\limits_a^b (f+cg)=\int\limits_a^b f+c\int\limits_a^b g</math>. {{משל}} | #<math>S(f+cg,P,P')=\sum_{k=1}^n (f+cg)(c_k)\Delta x_k=\sum_{k=1}^n f(c_k)\Delta x_k+c\sum_{k=1}^n g(c_k)\Delta x_k</math>. נשאיף <math>\lambda(P)\to0</math>. כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א <math>\lim_{\lambda(P)\to0} S(f+cg,P,P')=\int\limits_a^b f+c\int\limits_a^b g</math>. עצם קיום הגבול אומר ש-<math>f+cg</math> אינטגרבילית ולפי ערך הגבול נסיק <math>\int\limits_a^b (f+cg)=\int\limits_a^b f+c\int\limits_a^b g</math>. {{משל}} | ||
{{ | {{המשך סיכום|תאריך=1.3.11}} | ||
<ol start="2"> | <ol start="2"> | ||
<li>נתבונן בסכום רימן כלשהו עבור g: <math>\sum_{k=1}^n g(c_k)\Delta x_k</math>. לפי הנתון הוא קטן או שווה ל- <math>\sum_{k=1}^n f(c_k)\Delta x_k</math>. נשאיף <math>\lambda(P)\to0</math>. סכומים אלה שואפים לאינטגרלים של f ו-g ונסיק <math>\int\limits_a^b f\ge\int\limits_a^b g</math>. {{משל}}</li> | <li>נתבונן בסכום רימן כלשהו עבור g: <math>\sum_{k=1}^n g(c_k)\Delta x_k</math>. לפי הנתון הוא קטן או שווה ל- <math>\sum_{k=1}^n f(c_k)\Delta x_k</math>. נשאיף <math>\lambda(P)\to0</math>. סכומים אלה שואפים לאינטגרלים של f ו-g ונסיק <math>\int\limits_a^b f\ge\int\limits_a^b g</math>. {{משל}}</li> | ||
<li>נעיר ש-<math>\Omega</math> היא בעצם <math>\Omega(f)=\sup\{|f(x)-f(y)|:\ x,y\in[a,b]\}</math>. כזכור, אי שיוויון המשולש גורר ש-<math>\Big||f(x)|-|f(y)|\Big|\le|f(x)-f(y)|</math>. לכן <math>\Omega(|f|)=\ | <li>נעיר ש-<math>\Omega</math> היא בעצם <math>\Omega(f)=\sup\{|f(x)-f(y)|:\ x,y\in[a,b]\}</math>. כזכור, אי שיוויון המשולש גורר ש-<math>\Big||f(x)|-|f(y)|\Big|\le|f(x)-f(y)|</math>. לכן <math>\Omega(|f|)=\sup_{x,y\in[a,b]}\Big||f(x)|-|f(y)|\Big|\le\sup_{x,y\in[a,b]}|f(x)-f(y)|=\Omega(f)</math>. כעת תהי P חלוקה כלשהי של <math>[a,b]</math> ואז <math>\overline S(f,P)-\underline S(f,P)=\sum_{k=1}^n (M_k(f)-m_k(f))\Delta x_k</math>. נעיר שלכל f, <math>M_k(f)-m_k(f)</math> היא התנודה של f בקטע <math>[x_{k-1},x_k]</math> ולפי מה שהוכחנו זה גדול או שווה לתנודה של |f| באותו קטע: {{left|<math>\begin{align}\overline S(f,P)-\underline S(f,P)&=\sum_{k=1}^n \Big(M_k(f)-m_k(f)\Big)\Delta x_k\\&\ge\sum_{k=1}^n \Big(M_k(|f|)-m_k(|f|)\Big)\Delta x_k\\&=\overline S(|f|,P)-\underline S(|f|,P)\end{align}</math>}} | ||
כעת נוכיח ש-|f| אינטגרבילית. לצורך זה יהי <math>\varepsilon>0</math> נתון. כיוון ש-f אינטגרבילית (נתון) קיימת חלוקה P של <math>[a,b]</math> כך ש-<math>\overline S(|f|,P)-\underline S(|f|,P)\le\overline S(f,P)-\underline S(f,P)\to0</math> ונובע ממשפט 5 ש-|f| אינטגרבילית. נותר להוכיח את אי-השיוויון <math>\left|\int\limits_a^b f\right|\le\int\limits_a^b |f|</math>. לפי אי-שיוויון המשולש, לכל סכום רימן של f מתקיים <math>\left|\sum_{k=1}^n f(c_k)\Delta x_k\right|\le\sum_{k=1}^n |f(c_k)|\Delta x_k</math>. נשאיף <math>\lambda(P)\to0</math> ונקבל ש-<math>\left|\int\limits_a^b f\right|\le\int\limits_a^b|f|</math>. {{משל}}</li> | |||
<li>נתון <math>m\le f(x)\le M</math>. לפי משפט 1, לכל חלוקה P של <math>[a,b]</math> מתקיים <math>m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)</math>. נשאיף את <math>\lambda(P)\to0</math> כדי להסיק <math>m(b-a)\le\int\limits_a^b f\le M(b-a)</math>. אם נתון <math>|f(x)|\le M</math> אז נוכל להסתמך על סעיף 3 ומה שהוכחנו הרגע לומר <math>\left|\int\limits_a^b f\right|\le\int\limits_a^b |f|\le M(b-a)</math>. {{משל}}</li> | <li>נתון <math>m\le f(x)\le M</math>. לפי משפט 1, לכל חלוקה P של <math>[a,b]</math> מתקיים <math>m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)</math>. נשאיף את <math>\lambda(P)\to0</math> כדי להסיק <math>m(b-a)\le\int\limits_a^b f\le M(b-a)</math>. אם נתון <math>|f(x)|\le M</math> אז נוכל להסתמך על סעיף 3 ומה שהוכחנו הרגע לומר <math>\left|\int\limits_a^b f\right|\le\int\limits_a^b |f|\le M(b-a)</math>. {{משל}}</li> | ||
<li>לפי הנתון <math>M\le f(x)\le M</math>. לכן, עפ"י סעיף 4 <math>M(b-a)\le\int\limits_a^b f\le M(b-a)</math> ויש שיוויון. {{משל}}</li> | <li>לפי הנתון <math>M\le f(x)\le M</math>. לכן, עפ"י סעיף 4 <math>M(b-a)\le\int\limits_a^b f\le M(b-a)</math> ויש שיוויון. {{משל}}</li> | ||
</ol> | </ol> | ||
גרסה אחרונה מ־20:32, 29 ביולי 2012
האינטגרל לפי דרבו (המשך)
משפט 8
נניח ש-f מוגדרת וחסומה בקטע [math]\displaystyle{ [a,c] }[/math] ונניח ש-[math]\displaystyle{ a\lt b\lt c }[/math]. אזי f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וב-[math]\displaystyle{ [b,c] }[/math] אם"ם היא אינטגרבילית ב-[math]\displaystyle{ [a,c] }[/math], ואם כן מתקיים [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math].
הוכחה
[math]\displaystyle{ \implies }[/math]: נתונה f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וב-[math]\displaystyle{ [b,c] }[/math]. נקח חלוקה כלשהי P של [math]\displaystyle{ [a,b] }[/math] וחלוקה Q של [math]\displaystyle{ [b,c] }[/math] ונגדיר [math]\displaystyle{ R=P\cup Q }[/math] (כלומר R חלוקה של [math]\displaystyle{ [a,c] }[/math]). לכן מתקיים [math]\displaystyle{ \overline S(f,R)=\overline S(f,P)+\overline S(f,Q) }[/math]. נשאיף [math]\displaystyle{ \lambda(P),\lambda(Q)\to0 }[/math]. לפי הנתון [math]\displaystyle{ \overline S(f,P)\to\int\limits_a^b f }[/math] וגם [math]\displaystyle{ \overline S(f,Q)\to\int\limits_b^c f }[/math], לכן [math]\displaystyle{ \overline S(f,R)\to\int\limits_a^b f+\int\limits_b^c f }[/math]. באותו אופן נקבל [math]\displaystyle{ \underline S(f,R)\to\int\limits_a^b f+\int\limits_b^c f }[/math]. הראנו ש-[math]\displaystyle{ \overline S(f,R)-\underline S(f,R)\to0 }[/math] ולכן f אינטגרבילית ב-[math]\displaystyle{ [a,c] }[/math]. ע"פ משפט 4 נסיק [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math].
[math]\displaystyle{ \Longleftarrow }[/math]: נבחר חלוקות P,Q,R כמו בחלק הקודם, ושוב [math]\displaystyle{ \overline S(f,R)=\overline S(f,P)+\overline S(f,Q) }[/math] ו-[math]\displaystyle{ \underline S(f,R)=\underline S(f,P)+\underline S(f,Q) }[/math]. נחסיר ונקבל: [math]\displaystyle{ \overline S(f,R)-\underline S(f,R)=\overline S(f,P)-\underline S(f,P)+\overline S(f,Q)-\underline S(f,Q) }[/math]. כעת, אם [math]\displaystyle{ \varepsilon\gt 0 }[/math], האינטגרביליות של f על [math]\displaystyle{ [a,c] }[/math] גוררת שעבור [math]\displaystyle{ \lambda(P) }[/math] ו-[math]\displaystyle{ \lambda(Q) }[/math] מספיק קטנים [math]\displaystyle{ \overline S(f,P)-\underline S(f,P),\overline S(f,Q)-\underline S(f,Q)\lt \varepsilon }[/math]. קיום חלוקה P כזאת לכל [math]\displaystyle{ \varepsilon\gt 0 }[/math] מוכיח ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וקיום חלוקה Q - ב-[math]\displaystyle{ [b,c] }[/math]. השיוויון [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math] נובע מהחלק הקודם. [math]\displaystyle{ \blacksquare }[/math]
הכללה
אם [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math] ואם f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] אז [math]\displaystyle{ \int\limits_a^b f=\sum_{k=1}^n\int\limits_{x_{k-1}}^{x_k} f }[/math]. ההוכחה באינדוקציה.
מוסכמות:
- [math]\displaystyle{ \int\limits_a^a f=0 }[/math]
- אם [math]\displaystyle{ a\lt b }[/math] ואם f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] נרשום [math]\displaystyle{ \int\limits_b^a f=-\int\limits_a^b f }[/math]
(אלה מוסכמות ולא משפטים כי באופן שבו הגדרנו את האינטגרל עד עכשיו, [math]\displaystyle{ \int\limits_b^a }[/math] לא מוגדר עבור [math]\displaystyle{ a\le b }[/math])
עם מוסכמות אלה יתקיים:
[math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math] באופן בלתי תלוי בסדר של המספרים a,b,c. למשל, אם [math]\displaystyle{ c\lt a\lt b }[/math] אז לפי משפט 8 [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math]. נבדוק: [math]\displaystyle{ \int\limits_c^a f=-\int\limits_a^c f\ \and\ \int\limits_c^b f=-\int\limits_b^c f }[/math] ולכן [math]\displaystyle{ -\int\limits_b^c f=-\int\limits_a^c f+\int\limits_a^b f }[/math], מה שגורר [math]\displaystyle{ \int\limits_a^c f=\int\limits_a^b f+\int\limits_b^c f }[/math].
משפט 9
תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. עוד נניח ש-f רציפה ב-[math]\displaystyle{ (a,b] }[/math]. אזי f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math].
הוכחה
יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. נגדיר [math]\displaystyle{ c=a+\frac\varepsilon{2\Omega} }[/math]. לפי הנתון f רציפה ב-[math]\displaystyle{ [c,b] }[/math], אזי ממשפט 6 היא אינטגרבילית ב-[math]\displaystyle{ [c,b] }[/math], לכן נוכל לבחור חלוקה P של [math]\displaystyle{ [c,b] }[/math] כך ש-[math]\displaystyle{ \overline S(f,P)-\underline S(f,P)\lt \frac\varepsilon2 }[/math]. כעת נגדיר חלוקה Q של [math]\displaystyle{ [a,b] }[/math] ע"י [math]\displaystyle{ Q=\{a\}\cup P }[/math]. עוד נגדיר [math]\displaystyle{ M'=\sup\{f(x):\ a\le x\le c\} }[/math] וכן [math]\displaystyle{ m'=\inf\{f(x):\ a\le x\le c\} }[/math]. נובע כי
נובע ממשפט 4 ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math]. [math]\displaystyle{ \blacksquare }[/math]
מסקנה 1
המשפט נכון אם f חסומה ורציפה ב-[math]\displaystyle{ (a,b) }[/math].
מסקנה 2
נניח ש-f חסומה ב-[math]\displaystyle{ [a,b] }[/math] ורציפה שם פרט למספר סופי של נקודות [math]\displaystyle{ x_0,x_1,\dots,x_n }[/math] כך ש-[math]\displaystyle{ a\le x_0\lt x_1\lt \dots\lt x_n\le b }[/math]. אזי f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math].
הוכחה
עבור כל k נקבל ש-f חסומה ב-[math]\displaystyle{ [x_{k-1},x_k] }[/math] ורציפה ב-[math]\displaystyle{ (x_{k-1},x_k) }[/math]. לפי מסקנה 1, f אינטגרבילית ב-[math]\displaystyle{ [x_{k-1},x_k] }[/math]. נסתמך על ההכללה למשפט 8 לומר ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b]=\bigcup_{k=1}^n [x_{k-1},x_k] }[/math]. [math]\displaystyle{ \blacksquare }[/math]
הגדרה: אומרים ש-f "רציפה למקוטעין" ב-[math]\displaystyle{ [a,b] }[/math] אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון.
נובע ממסקנה 2 שכל פונקציה רציפה למקוטעין ב-[math]\displaystyle{ [a,b] }[/math] אינטגרבילית שם. באופן דומה אפשר להוכיח שאם f מוגדרת ו"מונוטונית למקוטעין" ב-[math]\displaystyle{ [a,b] }[/math] אז היא אינטגרבילית שם.
האינטגרל לפי רימן
הקדמה - הגישה של רימן
נניח ש-f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. נבחר חלוקה P של [math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math]. עוד נבחר לכל k מספר [math]\displaystyle{ c_k\in[x_{k-1},x_k] }[/math] ונכנה כ-P' את התת חלוקה [math]\displaystyle{ a\le c_1\lt c_2\lt \dots\lt c_n\le b }[/math]. ז"א [math]\displaystyle{ a=x_0\le c_1\le x_1\le c_2\le\dots\le c_n\le x_n=b }[/math]. בהתאם לכך נבנה סכום רימן [math]\displaystyle{ S(f,P,P')=\sum_{k=1}^n f(c_k)\Delta x_k }[/math] כאשר לכל k מתקיים [math]\displaystyle{ \Delta x_k=x_k-x_{k-1} }[/math].
[math]\displaystyle{ S(f,P,P') }[/math] מקרב את השטח שמתחת לגרף, אך לא ידוע אם הוא גדול, קטן או שווה לו.
נעיר שעל חלוקה אחת P של [math]\displaystyle{ [a,b] }[/math] אפשר לבנות אינסוף סכומי רימן [math]\displaystyle{ S(f,P,P') }[/math]. עם זאת, יתקיים תמיד [math]\displaystyle{ \underline S(f,P)\le S(f,P,P')\le\overline S(f,P) }[/math]. יתר על כן, [math]\displaystyle{ \underline S(f,P)=\inf_{P'} S(f,P,P') }[/math] ו-[math]\displaystyle{ \overline S(f,P)=\sup_{P'} S(f,P,P') }[/math].
הגדרת האינטגרל לפי רימן: תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. נאמר ש-f אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] אם כאשר [math]\displaystyle{ \lambda(P)\to0 }[/math] כל סכומי רימן [math]\displaystyle{ S(f,P,P') }[/math] שואפים לגבול אחד, שיסומן [math]\displaystyle{ \int\limits_a^b f }[/math].
משפט 10
תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. אזי f אינטגרבילית שם לפי רימן אם"ם f אינטגרבילית שם לפי דרבו, ואם כן אז [math]\displaystyle{ {\int\limits_R}_a^b f }[/math] (לפי רימן) [math]\displaystyle{ {\int\limits_D}_a^b f= }[/math] (לפי דרבו).
הוכחה
תחילה נניח ש-f אינטגרבילית לפי דרבו. נעיר שלכל חלוקה P ותת חלוקה P' של [math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ \underline S(f,P)\le S(f,P,P')\le\overline S(f,P) }[/math]. כעת נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math]. כיוון ש-f אינטגרבילית דרבו, [math]\displaystyle{ \overline S(f,P)\to{\int\limits_D}_a^b f }[/math] וכן [math]\displaystyle{ \underline S(f,P)\to{\int\limits_D}_a^b f }[/math] לכן משפט הסנדויץ' מבטיח ש-[math]\displaystyle{ \lim_{\lambda(P)\to0} S(f,P,P') }[/math] קיים ושווה ל-[math]\displaystyle{ {\int\limits_D}_a^b f }[/math]. ז"א f אינטגרבילית רימן ומתקיים [math]\displaystyle{ {\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P')={\int\limits_D}_a^b f }[/math].
לצד השני, נניח ש-f אינטגרבילית רימן. אזי מתקיים [math]\displaystyle{ {\int\limits_R}_a^b f=\lim_{\lambda(P)\to0} S(f,P,P') }[/math]. אם כן הוא גם שווה ל-[math]\displaystyle{ \lim_{\lambda(P)\to0} \sup_{P'} S(f,P,P')=\lim_{\lambda(P)\to0} \overline S(f,P)=\overline{\int}_a^b f }[/math],ובאופן דומה עבור אינטגרל תחתון (לפי דרבו, כמובן). מצאנו [math]\displaystyle{ {\int\limits_R}_a^b f=\overline{\int}_a^b f=\underline\int_a^b f }[/math]. עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם הוכחנו ש-[math]\displaystyle{ {\int\limits_R}_a^b f={\int\limits_D}_a^b f }[/math]. [math]\displaystyle{ \blacksquare }[/math]
משפט 11 (תכונות האינטגרל)
נניח ש-f ו-g מוגדרות ואינטגרביליות ב-[math]\displaystyle{ [a,b] }[/math], ונניח ש-c קבוע כלשהו. אזי:
- (לינאריות): [math]\displaystyle{ f+cg }[/math] אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] ומתקיים [math]\displaystyle{ \int\limits_a^b(f+cg)=\int\limits_a^b f+c\int\limits_a^b g }[/math].
- (מונוטוניות): אם [math]\displaystyle{ f(x)\ge g(x) }[/math] לכל [math]\displaystyle{ x\in[a,b] }[/math] אז [math]\displaystyle{ \int\limits_a^b f\ge\int\limits_a^b g }[/math]. (חיוביות): בפרט, אם [math]\displaystyle{ \forall x\in[a,b]:\ f(x)\ge0 }[/math] אז [math]\displaystyle{ \int\limits_a^b f\ge0 }[/math].
- (הכללה לאי-שיוויון המשולש): |f| אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math] וגם [math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b |f| }[/math].
- אם [math]\displaystyle{ m\le f(x)\le M }[/math] ב-[math]\displaystyle{ [a,b] }[/math] אז [math]\displaystyle{ m(b-a)\le\int\limits_a^b f\le M(b-a) }[/math] ואם [math]\displaystyle{ |f(x)|\le M }[/math] בקטע זה אז אז [math]\displaystyle{ \left|\int\limits_a^b f\right|\le M(b-a) }[/math].
- אם [math]\displaystyle{ f(x)=M }[/math] (פונקציה קבועה) אז [math]\displaystyle{ \int\limits_a^b f= M(b-a) }[/math].
הוכחה
- [math]\displaystyle{ S(f+cg,P,P')=\sum_{k=1}^n (f+cg)(c_k)\Delta x_k=\sum_{k=1}^n f(c_k)\Delta x_k+c\sum_{k=1}^n g(c_k)\Delta x_k }[/math]. נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math]. כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א [math]\displaystyle{ \lim_{\lambda(P)\to0} S(f+cg,P,P')=\int\limits_a^b f+c\int\limits_a^b g }[/math]. עצם קיום הגבול אומר ש-[math]\displaystyle{ f+cg }[/math] אינטגרבילית ולפי ערך הגבול נסיק [math]\displaystyle{ \int\limits_a^b (f+cg)=\int\limits_a^b f+c\int\limits_a^b g }[/math]. [math]\displaystyle{ \blacksquare }[/math]
את ההמשך עשינו בשיעור שאחריו:
- נתבונן בסכום רימן כלשהו עבור g: [math]\displaystyle{ \sum_{k=1}^n g(c_k)\Delta x_k }[/math]. לפי הנתון הוא קטן או שווה ל- [math]\displaystyle{ \sum_{k=1}^n f(c_k)\Delta x_k }[/math]. נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math]. סכומים אלה שואפים לאינטגרלים של f ו-g ונסיק [math]\displaystyle{ \int\limits_a^b f\ge\int\limits_a^b g }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- נעיר ש-[math]\displaystyle{ \Omega }[/math] היא בעצם [math]\displaystyle{ \Omega(f)=\sup\{|f(x)-f(y)|:\ x,y\in[a,b]\} }[/math]. כזכור, אי שיוויון המשולש גורר ש-[math]\displaystyle{ \Big||f(x)|-|f(y)|\Big|\le|f(x)-f(y)| }[/math]. לכן [math]\displaystyle{ \Omega(|f|)=\sup_{x,y\in[a,b]}\Big||f(x)|-|f(y)|\Big|\le\sup_{x,y\in[a,b]}|f(x)-f(y)|=\Omega(f) }[/math]. כעת תהי P חלוקה כלשהי של [math]\displaystyle{ [a,b] }[/math] ואז [math]\displaystyle{ \overline S(f,P)-\underline S(f,P)=\sum_{k=1}^n (M_k(f)-m_k(f))\Delta x_k }[/math]. נעיר שלכל f, [math]\displaystyle{ M_k(f)-m_k(f) }[/math] היא התנודה של f בקטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] ולפי מה שהוכחנו זה גדול או שווה לתנודה של |f| באותו קטע: [math]\displaystyle{ \begin{align}\overline S(f,P)-\underline S(f,P)&=\sum_{k=1}^n \Big(M_k(f)-m_k(f)\Big)\Delta x_k\\&\ge\sum_{k=1}^n \Big(M_k(|f|)-m_k(|f|)\Big)\Delta x_k\\&=\overline S(|f|,P)-\underline S(|f|,P)\end{align} }[/math]כעת נוכיח ש-|f| אינטגרבילית. לצורך זה יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. כיוון ש-f אינטגרבילית (נתון) קיימת חלוקה P של [math]\displaystyle{ [a,b] }[/math] כך ש-[math]\displaystyle{ \overline S(|f|,P)-\underline S(|f|,P)\le\overline S(f,P)-\underline S(f,P)\to0 }[/math] ונובע ממשפט 5 ש-|f| אינטגרבילית. נותר להוכיח את אי-השיוויון [math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b |f| }[/math]. לפי אי-שיוויון המשולש, לכל סכום רימן של f מתקיים [math]\displaystyle{ \left|\sum_{k=1}^n f(c_k)\Delta x_k\right|\le\sum_{k=1}^n |f(c_k)|\Delta x_k }[/math]. נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math] ונקבל ש-[math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b|f| }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- נתון [math]\displaystyle{ m\le f(x)\le M }[/math]. לפי משפט 1, לכל חלוקה P של [math]\displaystyle{ [a,b] }[/math] מתקיים [math]\displaystyle{ m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a) }[/math]. נשאיף את [math]\displaystyle{ \lambda(P)\to0 }[/math] כדי להסיק [math]\displaystyle{ m(b-a)\le\int\limits_a^b f\le M(b-a) }[/math]. אם נתון [math]\displaystyle{ |f(x)|\le M }[/math] אז נוכל להסתמך על סעיף 3 ומה שהוכחנו הרגע לומר [math]\displaystyle{ \left|\int\limits_a^b f\right|\le\int\limits_a^b |f|\le M(b-a) }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- לפי הנתון [math]\displaystyle{ M\le f(x)\le M }[/math]. לכן, עפ"י סעיף 4 [math]\displaystyle{ M(b-a)\le\int\limits_a^b f\le M(b-a) }[/math] ויש שיוויון. [math]\displaystyle{ \blacksquare }[/math]