עקיפה של אור: הבדלים בין גרסאות בדף
אין תקציר עריכה |
|||
| שורה 8: | שורה 8: | ||
נרשום משוואות עבור שני גלים <math>Y_1</math> ו-<math>Y_2</math> במיקום מסויים: | נרשום משוואות עבור שני גלים <math>Y_1</math> ו-<math>Y_2</math> במיקום מסויים: | ||
<math>Y_1=A_1 \sin (\omega t+\theta_1)</math> | <math>Y_1=A_1 \sin (\omega t+ \theta_1)</math> | ||
<math>Y_2=A_2 \sin (\omega t+\theta_2)</math> | <math>Y_2=A_2 \sin (\omega t+ \theta_2)</math> | ||
<math>A_1,A_2</math> אמפליטודת הגלים, <math>\omega</math> המהירות הזויתית ו-<math>\theta_1, \theta_2</math> הפאזות ההתחלתיות של הגלים. | <math>A_1,A_2</math> אמפליטודת הגלים, <math>\omega</math> המהירות הזויתית ו-<math>\theta_1, \theta_2</math> הפאזות ההתחלתיות של הגלים. | ||
| שורה 17: | שורה 17: | ||
<math>Y_1+Y_2=A_1 \sin (\omega t+\theta_1)+A_2 \sin (\omega t+\theta_2)</math> | <math>Y_1+Y_2=A_1 \sin (\omega t+\theta_1)+A_2 \sin (\omega t+\theta_2)</math> | ||
* עבור <math>\Delta\theta=\theta_1-theta_2=0</math> נקבל <math>A=A_1+A_2</math> . כלומר, האמפליטודה השקולה שווה לסכום האמפליטודה של המרכיבים (התאבכות בונה). | * עבור <math>\Delta\theta=\theta_1-\theta_2=0</math> נקבל <math>A=A_1+A_2</math> . כלומר, האמפליטודה השקולה שווה לסכום האמפליטודה של המרכיבים (התאבכות בונה). | ||
* עבור <math>\Delta\theta=\theta_1-theta_2=\pi</math> נקבל <math>A=A_1-A_2</math> . כלומר, האמפליטודה השקולה שווה להפרש האמפליטודה של המרכיבים (התאבכות הורסת). | * עבור <math>\Delta\theta=\theta_1-\theta_2=\pi</math> נקבל <math>A=A_1-A_2</math> . כלומר, האמפליטודה השקולה שווה להפרש האמפליטודה של המרכיבים (התאבכות הורסת). | ||
במקרה מיוחד של התאבכות הורסת, כאשר שתי האמפליטודות שוות, נקבל מקרה בו <math>A=0</math> , כלומר בנקודה לא יהיה אור. | במקרה מיוחד של התאבכות הורסת, כאשר שתי האמפליטודות שוות, נקבל מקרה בו <math>A=0</math> , כלומר בנקודה לא יהיה אור. | ||
| שורה 47: | שורה 47: | ||
המערכת כוללת לייזר חצי-מוליך, גלאי אור (Light sensor) וחיישן סיבוב(Rotary motion sensor) . קריאת הנתונים ורישומם מתבצעים בעזרת מערכת SW interface 750של DataStudio. | המערכת כוללת לייזר חצי-מוליך, גלאי אור (Light sensor) וחיישן סיבוב(Rotary motion sensor) . קריאת הנתונים ורישומם מתבצעים בעזרת מערכת SW interface 750של DataStudio. | ||
[[קובץ:מערכת הניסוי עקיפה.png| | [[קובץ:מערכת הניסוי עקיפה.png|700px|מרכז|ממוזער|איור 3 - מערכת הניסוי]] | ||
גלאי האור ניתן להזזה על- גבי פס המיוחד לכך. ההזזה מתבצעת באופן ידני, כאשר חיישן הסיבוב מודד את גודל התזוזה. לצורך זה, יש להפעיל את חיישן התזוזה במצב של מדידת מרחק לינארי (Position), זאת ע"י כניסה לתפריט Measurement של החיישן. | גלאי האור ניתן להזזה על- גבי פס המיוחד לכך. ההזזה מתבצעת באופן ידני, כאשר חיישן הסיבוב מודד את גודל התזוזה. לצורך זה, יש להפעיל את חיישן התזוזה במצב של מדידת מרחק לינארי (Position), זאת ע"י כניסה לתפריט Measurement של החיישן. | ||
גרסה מ־16:01, 23 באוקטובר 2014
ניסוי עקיפה מסדקים בוצע ב-1801, על ידי הפיזיקאי תומאס יאנג, על מנת להכריע האם האור הוא גל או חלקיק. בניסוי, התקבלה התנהגות גלית של האור (התאבכות ועקיפה), ובעקבות כך, במשך כל המאה ה-19, עד לניסוי פרנק-הרץ והמאמר על האפקט הפוטואלקטרי של אלברט איינשטיין, ההנחה המקובלת הייתה שהאור הוא גל. בניסוי זה נמדוד את עצמת האור הנפלט מלייזר חצי מוליך, לאחר מעבר האלומה דרך סדק בודד, שני סדקים ושריג עקיפה. בנוסף, נמדוד את התופעה ההפוכה בה מתרחשת עקיפה לאחר מעבר אלומת האור מחסומים דקים. באמצעות תבניות העקיפה וההתאבכות המתקבלות נמצא את אורך הגל של קרינת הליזר ואת וחב המחסומים אותם עבר האור.
רקע תיאורטי
האור הנראה יכול להיות מתואר על ידי תנועה של גלים אלקטרומגנטים בעלי אורך גל, אמפליטודה ופאזה. ככל גל, מתאפיינים גלי האור בתדירות, [math]\displaystyle{ f }[/math] , משרעת, [math]\displaystyle{ A }[/math], מהירות, [math]\displaystyle{ v }[/math], ואורך גל, [math]\displaystyle{ λ }[/math]. תדירות הגל תלוייה במקור, מהירות הגל תלוייה בתווך בו עובר הגל והיחס בינהם הוא התדר [math]\displaystyle{ f=v/λ }[/math]. עקרון הסופרפוזיציה קובע שכאשר בתווך מסוים עוברים מספר גלים בו-זמנית מתקבל גל שקול אשר שווה לסכום הגלים העוברים בתווך. כלומר, כל הגדלים המאפיינים את הגלים מתחברים לפי כללי החיבור הווקטורי. נדון עתה בסופר-פוזיציה (סכימה) של שני גלים הרמונים, בעלי תדירות שווה בנקודה מסוימת של המרחב. נרשום משוואות עבור שני גלים [math]\displaystyle{ Y_1 }[/math] ו-[math]\displaystyle{ Y_2 }[/math] במיקום מסויים:
[math]\displaystyle{ Y_1=A_1 \sin (\omega t+ \theta_1) }[/math] [math]\displaystyle{ Y_2=A_2 \sin (\omega t+ \theta_2) }[/math]
[math]\displaystyle{ A_1,A_2 }[/math] אמפליטודת הגלים, [math]\displaystyle{ \omega }[/math] המהירות הזויתית ו-[math]\displaystyle{ \theta_1, \theta_2 }[/math] הפאזות ההתחלתיות של הגלים.
לפי עקרון הסופר פוזיציה התנועה השקולה באותה נקודה נראית כמו:
[math]\displaystyle{ Y_1+Y_2=A_1 \sin (\omega t+\theta_1)+A_2 \sin (\omega t+\theta_2) }[/math]
- עבור [math]\displaystyle{ \Delta\theta=\theta_1-\theta_2=0 }[/math] נקבל [math]\displaystyle{ A=A_1+A_2 }[/math] . כלומר, האמפליטודה השקולה שווה לסכום האמפליטודה של המרכיבים (התאבכות בונה).
- עבור [math]\displaystyle{ \Delta\theta=\theta_1-\theta_2=\pi }[/math] נקבל [math]\displaystyle{ A=A_1-A_2 }[/math] . כלומר, האמפליטודה השקולה שווה להפרש האמפליטודה של המרכיבים (התאבכות הורסת).
במקרה מיוחד של התאבכות הורסת, כאשר שתי האמפליטודות שוות, נקבל מקרה בו [math]\displaystyle{ A=0 }[/math] , כלומר בנקודה לא יהיה אור.
ידוע שעוצמת הגל [math]\displaystyle{ I }[/math] פרופורציוניות לריבוע האמפליטודה, לכן במקרה הספציפי בו [math]\displaystyle{ A_1=A_2 }[/math] נקבל :
[math]\displaystyle{ I={A^2}={{A_1}^2\cos({{\Delta \theta} \over 2})} }[/math]
כלומר עוצמת הגל (האור) הנוצרת בסופרפוזיציה של שני גלים בעלי תדירות שווה תלויה בהפרש הפאזות בין הגלים הנפגשים.
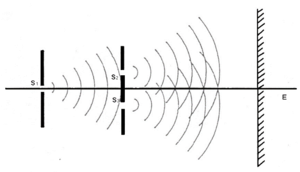
בניסוי של התאבכות משני סדקים משתמשים במקור אור אחד העובר דרך שני סדקים דקים הרחוקים מרחק [math]\displaystyle{ d }[/math] ביניהם. בצורה כזו ניתן לקבל שני מקורות אור קוהרנטים (ללא הפרש פאזה ביניהם), ראו איור 1.
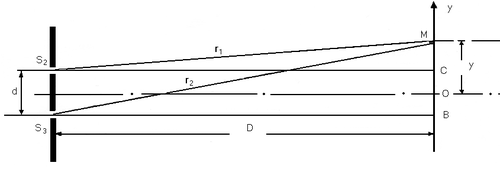
איור 2 מציג סכמה המאפשרת לעקוב אחר נקודה אקראית [math]\displaystyle{ M }[/math] על מסך רחוק מרחק [math]\displaystyle{ D }[/math] מהסדקים. נקבל כי עצמת האור המגיע לנקודה משני הסדקים תלוי בהפרש הדרכים [math]\displaystyle{ r_1-r_2 }[/math] אותן עברו הקרנים. מדמיון משולשים ומהנחה שמרחק המסך גדול מאוד מהמרחק בין הסדקים נקבל כי [math]\displaystyle{ r_1-r_2={yd \over D} }[/math].
כאמור כאשר הפרשי הפאזות שווים ל-0 או לאורכי גל שלמים נקבל התאבכות בונה לכן מקסימום אור ייראה על המסך במרחק [math]\displaystyle{ y_m }[/math] מהנקודה [math]\displaystyle{ O }[/math], כאשר:
[math]\displaystyle{ {{y_md} \over D} = m \lambda }[/math]
עקיפה מסדק בודד מוסברת על ידי עקרון הויגינס הקובע כי ניתן להתייחס לכל נקודה בחזית גל (המוגדר כמשטח של נקודות שוות פאזה) כאל מקור חדש של גל כדורי המתפשט לכל הכיוונים במהירות ההתפשטות של הגל המקורי. מקורות אלו מתאבכים ויוצרים תבנית עקיפה בה מינמום אור מתקבל בזויות [math]\displaystyle{ theta }[/math] מהציר המרכזי המקיימות [math]\displaystyle{ \sin \theta_n={{n \lambda} \over a} }[/math], כאשר [math]\displaystyle{ a }[/math] הוא רוחב הסדק.
מערכת הניסוי
המערכת כוללת לייזר חצי-מוליך, גלאי אור (Light sensor) וחיישן סיבוב(Rotary motion sensor) . קריאת הנתונים ורישומם מתבצעים בעזרת מערכת SW interface 750של DataStudio.
גלאי האור ניתן להזזה על- גבי פס המיוחד לכך. ההזזה מתבצעת באופן ידני, כאשר חיישן הסיבוב מודד את גודל התזוזה. לצורך זה, יש להפעיל את חיישן התזוזה במצב של מדידת מרחק לינארי (Position), זאת ע"י כניסה לתפריט Measurement של החיישן. מצאו את רמות הרגישות המתאימות עבור גלאי האור, כך שהמדידה שתתקבל תהיה חלקה וכוללת את העוצמות הגבוהות (בניסוי הסדקים). גלאי האור מצויד גם במתג רגישות, יש להפעיל את הגלאי במצב בו המתג נמצא על 100. הלייזר מופעל באמצעות מתג הנמצא בצידו האחורי. בסמוך למתג זה נמצאות שתי ידיות לקביעת הכיוון המדוייק של קרן הלייזר.
מהלך הניסוי
התאבכות ועקיפה מסדקים
קבלו תבניות עקיפה עבור 3 סדקים ברוחב שונה. קבלו את תבנית ההתאבכות של שני סדקים בעובי ****. הציגו את תבנית ההתאבכות משני סדקים ביחד עם תבנית העקיפה מסדק בודד בעל אותו עובי בגרף אחד. מהי משמעותה של הצגה זו?
- מתוך תבניות אלו מצאו את אורך הגל של הלייזר.
עקיפה ממכשול צר
על פי עקרון Babinet , תמונת עקיפה ממכשול צר בעובי מסויים זהה לתמונת העקיפה מסדק באותו עובי. קבלו תמונות עקיפה עבור שני מכשולים בעוביים שונים, ועבור שערה אחת משערות ראשכם. שימו לב שבניסוי זה עצמת האור חזקה, לכן חיישן האור מגיע לרוויה והתמונה "תחתך" במרכז.
- מצאו בעזרת תבנית העקיפה המתקבלת את עובי המכשולים השונים.
השפעת רגישות החיישן על תוצאות המדידה
בניסוי זה ניתן לראות כיצד תמונת העקיפה משתנה מהותית עם שינוי רגישות חיישן האור. חלק זה של הניסוי מדגים את החשיבות בבחירת רגישות מתאימה למכשירי המדידה.
בצעו את הניסוי בשתי רגישויות מדידה, והסבירו את ההבדלים המתקבלים בתמונות העקיפה.