מערכי תרגול

• תרגול 1 הפרדת משתנים ומד"ר לינאריות מסדר ראשון

• תרגול 2 דוגמאות מד"ר מסדר ראשון. משוואות ברנולי, ריקטי וקלרו

• תרגול 3 מד"ר מסדר שני. מד"ר מסדר n - ורונסקיאן והורדת סדר

• תרגול 4 וריאציית המקדמים ופונקציית גרין

• תרגול 5 משוואה מאפיינת למד"ר מסדר n עם מקדמים קבועים(הניחוש של אוילר). אופרטורים דיפרנציאליים ושיטת המשמיד
• שיטת המשמיד/Annihilator Method סיכום ודוגמאות (אנגלית)

מבוססים בעיקר על התרגולים של מר מיכאל טויטו

הערות על התרגולים

תרגול 1 : לגבי שיטת הפרדת המשתנים ששאלתם בתרגול , ודאי ניתן הסבר מדויק בהרצאה ,ובכל זאת למי שקורא את מערך התרגול ומוצא את עצמו מבולבל כאילו כפלנו ב dx .

התחלנו ממשוואה מהצורה [math]\displaystyle{ y'=f(x)g(y) }[/math]

אותה יש לחלק ב [math]\displaystyle{ g(y) }[/math] ולעשות אינטגרל לפי x ,אז נקבל [math]\displaystyle{ \int \frac{y'dx}{g(y)} =\int f(x)dx }[/math]

כעת בהצבה [math]\displaystyle{ z=y(x) }[/math] נקבל [math]\displaystyle{ \int \frac{dz}{g(z)} =\int f(x)dx+c }[/math] ומכאן ניתן להמשיך .

בפרקטיקה אין בעיה ,ואפילו מומלץ, שתפתרו את התרגילים באותה הדרך שראינו בתרגול .

תרגול 2 : משוואת קלרו,אותה למדנו בסוף התרגול, הנה מקרה פרטי של משוואת לגרנז' [math]\displaystyle{ y=f(y')+xg(y') }[/math] ,אותה לא למדנו, כאשר [math]\displaystyle{ g(y')=y' }[/math] .

בנוסף, הנה תמונה יפה (באדיבות עידן אריה) למעטפת שקיבלנו עבור ישרים שמרחקם מהראשית הנו 1 ושעל ידי כך הגענו למשוואת קלרו עם [math]\displaystyle{ f(y')=\pm\sqrt{1+(y')^2} }[/math]

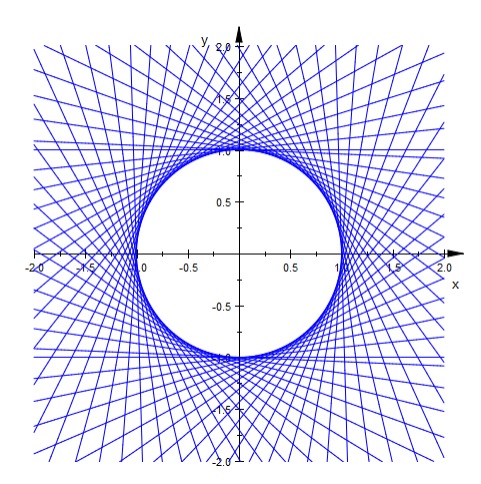
תרגול 3 : שימו לב לסכומים בצירוף הלינארי שאמורים להתחיל מ-1 ולא מ-0 . תיקנתי בקובץ .

טעות נוספת שתוקנה במהלך התרגול הנה בדוגמא שנתנו לכך שאם הורונסקיאן של n פונקציות מתאפס זה לא בהכרח גורר ש-n הפונקציות תלויות לינארית . בדוגמא לקחתי שתי פונקציות [math]\displaystyle{ x }[/math] ו [math]\displaystyle{ \left | x \right | }[/math] והבעיה היא ש [math]\displaystyle{ \left | x \right | }[/math] אינה גזירה ב-0 . לכן לקחנו את הפונקציות [math]\displaystyle{ x^3 }[/math] ו [math]\displaystyle{ \left | x^3 \right | }[/math]