אטום: הבדלים בין גרסאות בדף
Ofekgillon10 (שיחה | תרומות) אין תקציר עריכה |
Ofekgillon10 (שיחה | תרומות) |
||
| שורה 31: | שורה 31: | ||
בהתבססו על הנחות יסוד אלה, חישב בוהר את רדיוסי המסלולים המותרים של אטום המימן, את אנרגיות המצבים היציבים ואורכי הגל של קווי ספקטרום הפליטה או ספקטרום הבליעה המתאימים למעבר של האטום ממצב יציב אחד לאחר. | בהתבססו על הנחות יסוד אלה, חישב בוהר את רדיוסי המסלולים המותרים של אטום המימן, את אנרגיות המצבים היציבים ואורכי הגל של קווי ספקטרום הפליטה או ספקטרום הבליעה המתאימים למעבר של האטום ממצב יציב אחד לאחר. | ||
לפי החוק השני של ניוטון, לחלקיק בתנועה מעגלית יש תאוצה צנטריפטלית שכיוונה כלפי מרכז המעגל. לכן על החלקיק פועל כח צנטריפטלי שכיוונו למרכז וגדלו <math>F={mv^2 \over r}</math> , הכח המאלץ את האלקטרון לנוע במעגל סביב הגרעין הוא הכח החשמלי המושך אותו אל הגרעין. מהשוואת שני כוחות אלו נקבל את רדיוס המסלול: | ====פיתוח מתמטי==== | ||
לפי החוק השני של ניוטון, לחלקיק בתנועה מעגלית יש תאוצה צנטריפטלית שכיוונה כלפי מרכז המעגל. לכן על החלקיק פועל כח צנטריפטלי שכיוונו למרכז וגדלו <math>F={mv^2 \over r}</math> , הכח המאלץ את האלקטרון לנוע במעגל סביב הגרעין הוא הכח החשמלי <math>F=\frac{e^2}{4\pi \epsilon_0 r^2} </math> המושך אותו אל הגרעין (מטען האלקטרון מסומן ב-e). מהשוואת שני כוחות אלו נקבל את רדיוס המסלול: | |||
<math>r={e^2 \over {4 \pi \epsilon_0 m v^2}}</math> | <math>r={e^2 \over {4 \pi \epsilon_0 m v^2}}</math> | ||
| שורה 39: | שורה 40: | ||
הצבת ערכה של <math>v</math> ממשוואת התנאי למסלולים סטציונריים נותנת ערך בדיד לרדיוסים: | הצבת ערכה של <math>v</math> ממשוואת התנאי למסלולים סטציונריים נותנת ערך בדיד לרדיוסים: | ||
<math>mvr=n \frac{h}{2\pi} \Rightarrow v=\frac{n\cdot h}{2\pi m r}\ ,\ r={e^2 \over {4 \pi \epsilon_0 m v^2}}\Rightarrow r_n=({{\epsilon_0 h^2} \over {\pi me^2}})n^2</math> | |||
האנרגיה של האלקטרון בכל אחד מהמצבים הסטציונריים מורכבת מהאנרגיה הקינטית ומהאנרגיה הפוטנציאלית של האלקטרון והגרעין כלומר: | האנרגיה של האלקטרון בכל אחד מהמצבים הסטציונריים מורכבת מהאנרגיה הקינטית ומהאנרגיה הפוטנציאלית של האלקטרון והגרעין כלומר: | ||
גרסה מ־23:32, 1 באוקטובר 2015
בניסוי זה תלמדו על אחת מפריצות הדרך בדרך לבניית מכניקת הקוונטים.
בשנת 1913 הציג נילס בוהר את מודל האטום שלו, לפיו בתוך האטום אלקטרונים נעים במספר בדיד של מסלולים, שבהם התנע הזוויתי של האלקטרונים הוא בכפולות שלמות של קבוע פלאנק [math]\displaystyle{ h }[/math], חלקי [math]\displaystyle{ 2\pi }[/math]. המודל הזה הסביר באופן יפה את ספקטרום הפליטה של אטום המימן, וההסבר האינטואיטיבי שעומד מאחוריו הוא שהאלקטרון מתנהג כמו גל, והמסלולים בהם הוא יכול לנוע דומים למצבים עצמיים של גלים.
בניסוי זה תוכלו לקבוע את רמות האנרגיה של אטום המימן לפי קווי ספקטרום הפליטה שלו ולמצוא את קבוע רידברג (Rydberg). חלקו שני של הניסוי הוא ביצוע גירסא של ניסוי פרנק-הרץ למציאת פוטנציאל עירור ופוטנציאל יינון של אטומי גז אציל.
רקע תיאורטי
העשרה - קצת היסטוריה
בסוף המאה ה-19, אחרי שג'וזף תומסון הגיע בעקבנות ניסוי למסקנה שהאטום מורכב בתוכו ממטענים חיוביים ושליליים, התפרסם "מודל עוגת הצימוקים" שלו. לפי המודל, האטום מורכב ממטען חיובי שמפוזר בצורה אחידה ובתוכו תקועים אלקטרונים, נושאי מטען שלילי, כפי שצימוקים נמצאים בעוגה.
בתחילת המאה ה-20, הנס גייגר וארנסט מרסדן, תחת הדרכתו של ארנסט רתרפורד, ביצעו ניסוי בו מפגיזים מספר עלי מתכות שונות בחלקיקי אלפא, והצורה בה חלקיקי האלפא התפזרו מההפגזרות הייתה שונה מהמצופה לפי עוגת הצימוקים, ולפיכך יצאו במודל חדש לאטום: המודל הפלנטרי (מהמילה planet, כוכב לכת). לפי המודל הפלנטרי של רתרפורד, האטום מורכב מגרעין חיובי והאלקטרונים מקיפים אותו כמו שכוכבי הלכת מקיפים את השמש. המודל התאים לתוצאות הניסוי, אך היו בו מספר בעיות, הגדולה שבהן היא העובדה שאם האלקטרונים מסתובבים סביב הגרעין, הם בתאוצה, וידוע מחשמל שמטען בתאוצה פולט קרינה אלקטרומגנטית ומאבד אנרגיה (תראו את זה בקורס תורת שדות אלקטרומגנטיים בשנה ג'), ומכאן שאמור לקרוס אל גרעין האטום. חישובים מדויקים הראו שזמן הקריסה הוא פחות משנייה, וכפי שידוע לנו אטומים הם דברים יציבים, כך שהמודל הפלנטרי נפל גם הוא.
כמו כן, כאשר לכדו גזים מסוימים וחיממו אותם, גילו שהם פולטים אור. יתר על כן, כאשר הסתכלו על האור דרך ספקטרומטר, מכשיר שמפצל את התדרים השונים של האור, ראו שבמקום ספקטרום רציף של צבעים, האור מורכב מכמה צבעים ספציפיים. כלומר ספקטרום הפליטה שלהם היה בדיד (או במילה אחרת, "מֵקְווּנְטַט"), דבר שנראה מאוד מוזר משום שקלאסית, אין שום סיבה שמשהו יפלוט רק צבעים מסוימים.
מודל האטום של בוהר
עקב נפילתו של המודל הפלנטרי של רתרפורד, בשנת 1913 הציע נילס בוהר (N.Bohr), פיזיקאי דני צעיר שעבד במעבדתו של רתרפורד מודל מתוקן. הנחות בוהר הן עבור אטום המימן שהוא האטום הפשוט ביותר – בו יש אלקטרון אחד המסתובב מסביב לגרעין המכיל פרוטון בודד.
- אלקטרון יכול לנוע מסביב לגרעין רק במסלולים מעגליים מסויימים (המסלולים "מֵקְווּנְטַטִים"). כאשר האלקטרון נע באחד מהמסלולים הללו, אין הוא פולט קרינה אלקטרומגנטית למרות תנועתו המואצת. הנחה זו מנוגדת לחוקי הפיזיקה הקלאסית ובוהר קיבל אותה כאקסיומה.
כפי שכתוב בהקדמה, בוהר קבע שהתנאי למסלולים המותרים (נקראים גם סטציונריים) הוא שהתנע הזוויתי [math]\displaystyle{ L= r \times p = rmv }[/math] הוא כפולה שלמה של [math]\displaystyle{ \frac{h}{2\pi} }[/math] (כלומר לא כל תנע זוויתי אפשרי, אלא ערכים בדידים של תנע זוויתי, מכאן שגם הוא מקוונטט):
[math]\displaystyle{ mvr=n {h \over 2 \pi} }[/math] כאשר: [math]\displaystyle{ m }[/math]- מסת האלקטרון, [math]\displaystyle{ h }[/math]-קבוע פלנק ו- [math]\displaystyle{ n }[/math] מספר טבעי המאפיין את אינדקס המסלול.
- מההנחה הקודמת וממכניקה אפשר להבין שלאלקטרון שמסתובב במעגל ברדיוס [math]\displaystyle{ n }[/math] סביב הגרעין תהיה אנרגיה [math]\displaystyle{ E_n }[/math] מתאימה. לפי בוהר, האלקטרון יכול לקפוץ ממסלול למסלול אבל צריך לקבל או לפלוט מנת אנרגיה מתאימה, היא נבלעת או נפלטת בצורת פוטון. למדתם בפיזיקה מודרנית שאנרגיה של פוטון בתדירות [math]\displaystyle{ f }[/math] היא [math]\displaystyle{ hf }[/math] ומכאן שכאשר אלקטרון עובר ממסלול n למסלול m הוא צריך לפלוט או לבלוע פוטון בתדר שמקיים:
[math]\displaystyle{ hf=|E_n-E_m| }[/math]
בהתבססו על הנחות יסוד אלה, חישב בוהר את רדיוסי המסלולים המותרים של אטום המימן, את אנרגיות המצבים היציבים ואורכי הגל של קווי ספקטרום הפליטה או ספקטרום הבליעה המתאימים למעבר של האטום ממצב יציב אחד לאחר.
פיתוח מתמטי
לפי החוק השני של ניוטון, לחלקיק בתנועה מעגלית יש תאוצה צנטריפטלית שכיוונה כלפי מרכז המעגל. לכן על החלקיק פועל כח צנטריפטלי שכיוונו למרכז וגדלו [math]\displaystyle{ F={mv^2 \over r} }[/math] , הכח המאלץ את האלקטרון לנוע במעגל סביב הגרעין הוא הכח החשמלי [math]\displaystyle{ F=\frac{e^2}{4\pi \epsilon_0 r^2} }[/math] המושך אותו אל הגרעין (מטען האלקטרון מסומן ב-e). מהשוואת שני כוחות אלו נקבל את רדיוס המסלול:
[math]\displaystyle{ r={e^2 \over {4 \pi \epsilon_0 m v^2}} }[/math]
כאשר [math]\displaystyle{ \epsilon_0=8.85*10^{-12} Fm^{-1} }[/math] הוא הקבוע הדיאלקטרי של החלל החופשי.
הצבת ערכה של [math]\displaystyle{ v }[/math] ממשוואת התנאי למסלולים סטציונריים נותנת ערך בדיד לרדיוסים:
[math]\displaystyle{ mvr=n \frac{h}{2\pi} \Rightarrow v=\frac{n\cdot h}{2\pi m r}\ ,\ r={e^2 \over {4 \pi \epsilon_0 m v^2}}\Rightarrow r_n=({{\epsilon_0 h^2} \over {\pi me^2}})n^2 }[/math]
האנרגיה של האלקטרון בכל אחד מהמצבים הסטציונריים מורכבת מהאנרגיה הקינטית ומהאנרגיה הפוטנציאלית של האלקטרון והגרעין כלומר:
[math]\displaystyle{ E_T=E_p+E_k=-{e^2 \over {4 \pi \epsilon_0 r}}+{{mv^2} \over 2} }[/math]
נקבל לאחר הצבת הרדיוס ואלגברה פשוטה כי מסלולי האנרגיה מקוונטטים ושווים:
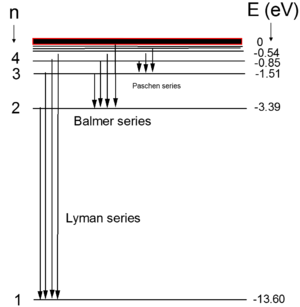
[math]\displaystyle{ E_n=-{{e^4m} \over {8 \pi \epsilon_0 r}}=-{{hcR} \over n^2} }[/math]
כאשר [math]\displaystyle{ R={{e^4m} \over {8 \epsilon_0 ^2 h^3c}} }[/math] קבוע רידברג (Rydberg)
מתוך ביטוי זה ניתן לשרטט את רמות האנרגיה של אטום המימן (ראו איור 1).
הקווים הספקטרליים של אטומי המימן יוצרים מספר סדרות המתאימות למעברים של האטום מרמת אנרגיה גבוהה (n) לנמוכות יותר (m). סדרות אלו קיבלו שמות של המדענים: Lyman, Balmer, , Paschen, Brackett, Pfund.
בעבודה זו נשתמש בסדרת Balmer כי בסדרה זו קוי הספקטרום המתקבלים הם בתחום הנראה. מודל בוהר נותן במדוייק את הקווים הספקטרליים של אטום המימן או דמוי מימן – שבקליפתו החיצונית אלקטרון אחד בלבד, אך נכשל במקרים אחרים. לתיאור אטומים בעלי מספר אלקטרונים, יש להשתמש בתיאור הקוונטי המלא של האטום – לפי משוואת שרדינגר.
ניסוי פרנק-הרץ (Franck–Hertz)
במעבדה זו נחזור על אחת הגרסאות של ניסוי פרנק-הרץ (James Franck – Gustav Hertz), אשר הפכו לאחת ההוכחות הניסיוניות הראשונות למודל בוהר המהווה יסוד לפיסיקה הקוונטית. פרס נובל לפיסיקה הוענק לגוסטב הרץ וג'יימס פרנק עבור ניסויים אלה ב-1925.
פוטנציאלים של עירור (excitation) ויינון (ionization)
בליעת אנרגיה ע"י אטום ומעבר האטום למצב סטציונרי בעל אנרגיה גדולה יותר נקרא עירור. אנרגית העירור מבוטאת בדרך כלל ביחידות אלקטרון-וולט (eV). על מנת לקבוע את המצבים הסטציונריים ניתן להשתמש בהפצצת אטומים באלקטרונים. כאשר האנרגיה של אלקטרונים נמוכה, ההתנגשויות עם האטומים הן אלסטיות. כתוצאה מהבדל גדול במסות של האלקטרונים והאטומים, האלקטרונים מעבירים לאטומים רק חלק קטן מהאנרגיה שלהם. אולם כשהאנרגיה מגיעה לערך מסוים ההתנגשויות כבר אינן אלסטיות: אלקטרונים מוסרים לאטומים את כל האנרגיה שלהם, והאטומים עוברים למצב בעל אנרגיה גדולה יותר. ניסוים אלה מוכיחים את קיומם של מצבים סטציונריים באטום ומאפשרים למדוד את האנרגיות שלהם. אם אנרגית האלקטרונים מספיק גדולה, מתרחש יינון האטום - בריחת אלקטרון אחד מאטום והפיכת האטום ליון.
מערכת הניסוי
ספקטרום הפליטה של מימן
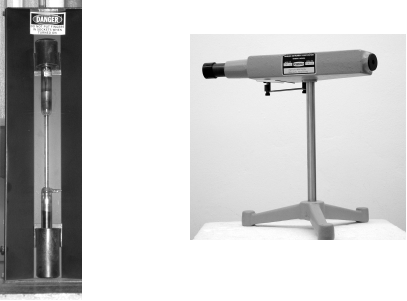
המערכת מורכבת ממנורת מימן הפועלת תחת מתח של [math]\displaystyle{ 5000V }[/math]. אטומי המימן מעוררים ופולטים קרינת אור נראה. כדי למצוא את אורכי הגל של האור הנפלט נשתמש בספקטרוסקופ, ראו איור 2. בספקטרומטר, האור הנפלט מהמימן החם עובר דרך שריג עקיפה ויוצר תמונת התאבכות. בתמונה זו מופרדים הגלים לפי אורך הגל שלהם, ועל ידי כיול ניתן לראות את סדרת אורכי הגל של הקרינה הנפלטת.
ניסוי פרנק-הרץ
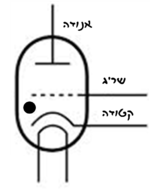
בניסוי שלנו נחזור על אחת הגרסאות של ניסוי פרנק-הרץ. נשתמש בשפופרת תיראטרון (thyratron)- טריאודה ממולאת גז עם קתודה מחוממת הפולטת אלקטרונים. בין האנודה לקטודה ישנו שריג (grid) שצורתו המחוררת מאפשרת מעבר אלקטרונים דרכו. מתח מאיץ מופעל בין השריג לבין הקתודה של התיראטרון ושולט על תנועת האלקטרונים (ראו איור 2).
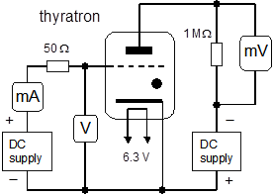
מעגל המדידה מסורטט באיור 4. במערכת זו מפעילים מתח שלילי על האנודה (אלקטרודה המשמשת כקולט), כך שאלקטרונים אינם יכולים להגיע אליו. בישומים רגילים של תיראטרון האנודה מוחזקת בפוטנציאל חיובי על מנת לקלוט את האלקטרונים.
הזרם במעגל הקולט נוצר כאשר מתבצע עירור באטומי הגז שבשפופרת באופן הבא: האלקטרונים אשר נפלטים מהקתודה המחוממת ומואצים לעבר השריג (בשל הפוטנציאל החיובי) מתנגשים עם אטומי הגז שבשפופרת. בשלב הראשוני ההתנגשויות הינם אלסטיות כך שהאלקטרונים כמעט ולא מאבדים מהאנרגיה שלהם וממשיכים לעבר השריג. גם האלקטרונים המצליחים לעבור את השריג חוזרים בחזרה אליו בשל הפוטנציאל השלילי של הקולט. כאשר האנרגיה הקינטית של האלקטרונים (בשל הגדלת הפוטנציאל), שווה לרמת האנרגיה של אטומי הגז מתבצע עירור של האטומים. האלקטרונים מוסרים את האנרגיה שלהם לאטומים ובככך גורמים לאלקטרוני אטומי-הגז לעבור למסלול סטציונרי בעל אנרגיה גבוהה יותר. לאחר פרק זמן קצר מאוד, האלקטרונים חוזרים למצב בעל אנרגיה יותר נמוכה, ופולטים פוטונים. פוטונים אלו פוגעים בקולט וגורמים לאפקט הפוטו-אלקטרי. פוטונים משחררים אלקטרונים מהקולט (אנרגית הפוטונים גדולה פונקציית העבודה של הקולט). אלקטרונים אלה נעים מהקולט לעבר השריג וכך נוצר הזרם במעגל הקולט.
הזרם במעגל הקולט נמדד בעזרת מכשיר בעל רגישות בסדר גודל של [math]\displaystyle{ 10^{-10} A }[/math]. במערכת שלנו במעגל הקולט קיים נגד של [math]\displaystyle{ 1 M \Omega }[/math], כאשר מודדים עליו את מפל מתח עליו מבאמצעות מילי-וולטמטר בעל רגישות של [math]\displaystyle{ 0.1mV }[/math], סך כל הרגישות בזרם הנמדד תהיה [math]\displaystyle{ 10^{-10} A }[/math].
פוטנציאל העירור של אטומי הגז בתיראטרון שווה למתח המאיץ שעבורו מופיע זרם במעגל של הקולט. את פוטנציאל היינון קובעים לפי עלייה חזקה בזרם השריג. עלייה זאת קשורה לנטרול של המטען האלקטרוני המרחבי ליד הקתודה על ידי היונים החיוביים שהופיעו. על מנת להגביל את זרם השריג, הוכנסה התנגדות למעגל.
מהלך הניסוי
ספקטרום הפליטה של מימן
את המערכת יפעיל ויכבה המדריך בלבד!
סכנה! המנורה פועלת תחת מתח של [math]\displaystyle{ 5000 V }[/math]! אין לקרב אל המנורה חפצים מתכתיים או ידיים.
יש להסתכל דרך הספקטרוסקופ ולמצוא את אורכי הגל של 3 הקווים הברורים ביותר. ניתן לראות עוד קווים חלשים יותר – כתוצאה ממולקולות מימן.
- חשבו את ערכו הממוצע של קבוע רידברג עבור 3 אורכי הגל המתקבלים.
- שרטטו תרשים של רמות האנרגיה לפי המדידות והחישובים שביצעתם.
ניסוי פרנק–הרץ
בנו את המעגל באיור כאשר המתח השלילי על הקולט הוא [math]\displaystyle{ 5 V }[/math]. ומצאו את אופייני הזרם בקולט ובשריג כפונקציה של המתח על השריג. התחל ממתח של [math]\displaystyle{ 0.5 V }[/math] ועלו בחצאי וולטים. דונו בתוצאות המתקבלות וחשבו את אורך הגל של האור הנפלט.