אורך עקומה: הבדלים בין גרסאות בדף
מ (משעמם לי.) |
יהודה שמחה (שיחה | תרומות) מאין תקציר עריכה |
||
| שורה 1: | שורה 1: | ||
[[קובץ:קירוב אורך גרף.png|ימין|300px]] | [[קובץ:קירוב אורך גרף.png|ימין|300px]] | ||
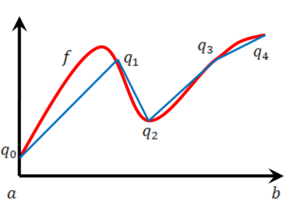
תהי f פונקציה גזירה ברציפות בקטע סגור <math>[a,b]</math>. נקרב את אורך העקומה שלה (אורך הקו שלה בגרף) על ידי גבול סכום המיתרים בין נקודות הפונקציה על חלוקות (סכום הקווים הכחולים בציור). | תהי <math>f</math> פונקציה גזירה ברציפות בקטע סגור <math>[a,b]</math>. נקרב את אורך העקומה שלה (אורך הקו שלה בגרף) על-ידי גבול סכום המיתרים בין נקודות הפונקציה על חלוקות (סכום הקווים הכחולים בציור). | ||
עבור חלוקת הקטע <math>P=\{x_0, | עבור חלוקת הקטע <math>P=\{x_0,\ldots,x_n\}</math>, הנוסחא לסכום המיתרים נתונה על-ידי: | ||
{{left|<math>\begin{align}L(P)&=\sum_{k=1}^n\sqrt{(x_{k-1}-x_k)^2+\big(f(x_k)-f(x_{k-1})\big)^2}\\&=\sum_{k=1}^n\sqrt{1+\left(\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}\right)^2}\ (x_k-x_{k-1})\\&=\sum_{k=1}^n\sqrt{1+f'(c_k)^2}\Delta x_k\end{align}</math>}} | |||
כאשר הנקודות <math>c_k</math> מקיימות <math>\forall k:\ c_k\in(x_{k-1},x_k)</math>. אכן קיימות נקודות כאלה לפי משפט לגראנז'. | כאשר הנקודות <math>c_k</math> מקיימות <math>\forall k:\ c_k\in(x_{k-1},x_k)</math>. אכן קיימות נקודות כאלה לפי משפט לגראנז'. | ||
הגענו לסכום רימן עבור הפונקציה <math>\sqrt{1+f'(x)^2}</math>. כיון שנתון כי <math>f'(x)</math> רציפה, גם <math>\sqrt{1+f'(x)^2}</math> רציפה בקטע הסגור ולכן אינטגרבילית. | |||
על כן סכומי רימן אלה שואפים לאינטגרל <math>\displaystyle\int\limits_a^b \sqrt{1+f'(x)^2}\ dx</math> וזוהי הנוסחא לחישוב אורך עקום של פונקציה. | |||
על כן סכומי רימן אלה שואפים לאינטגרל <math>\int\limits_a^b\sqrt{1+f'(x)^2}\ | |||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
גרסה מ־16:57, 27 בינואר 2016
תהי [math]\displaystyle{ f }[/math] פונקציה גזירה ברציפות בקטע סגור [math]\displaystyle{ [a,b] }[/math]. נקרב את אורך העקומה שלה (אורך הקו שלה בגרף) על-ידי גבול סכום המיתרים בין נקודות הפונקציה על חלוקות (סכום הקווים הכחולים בציור).
עבור חלוקת הקטע [math]\displaystyle{ P=\{x_0,\ldots,x_n\} }[/math], הנוסחא לסכום המיתרים נתונה על-ידי:
כאשר הנקודות [math]\displaystyle{ c_k }[/math] מקיימות [math]\displaystyle{ \forall k:\ c_k\in(x_{k-1},x_k) }[/math]. אכן קיימות נקודות כאלה לפי משפט לגראנז'.
הגענו לסכום רימן עבור הפונקציה [math]\displaystyle{ \sqrt{1+f'(x)^2} }[/math]. כיון שנתון כי [math]\displaystyle{ f'(x) }[/math] רציפה, גם [math]\displaystyle{ \sqrt{1+f'(x)^2} }[/math] רציפה בקטע הסגור ולכן אינטגרבילית.
על כן סכומי רימן אלה שואפים לאינטגרל [math]\displaystyle{ \displaystyle\int\limits_a^b \sqrt{1+f'(x)^2}\ dx }[/math] וזוהי הנוסחא לחישוב אורך עקום של פונקציה.