משפט ערך הממוצע האינטגרלי: הבדלים בין גרסאות בדף
| (2 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
=ממוצע אינטגרלי= | ==ממוצע אינטגרלי== | ||
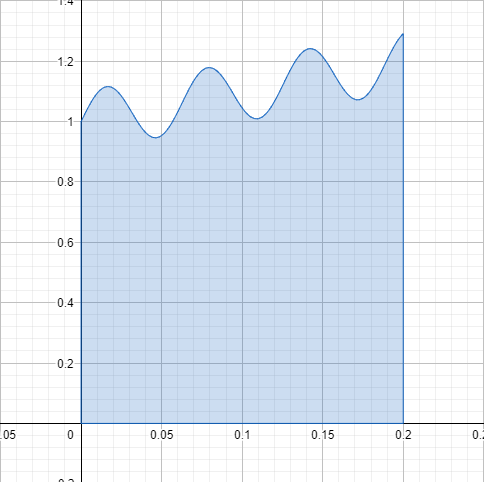
כיצד הייתם מגדירים את גובה המים הממוצע בבריכה הבאה? | כיצד הייתם מגדירים את גובה המים הממוצע בבריכה הבאה? | ||
| שורה 8: | שורה 8: | ||
אמנם יש [[אי-שוויון הממוצעים|דרכים רבות]] להגדיר ממוצע, אך אנחנו נתאר דרך אחת. | אמנם יש [[אי-שוויון הממוצעים|דרכים רבות]] להגדיר ממוצע, אך אנחנו נתאר דרך אחת. | ||
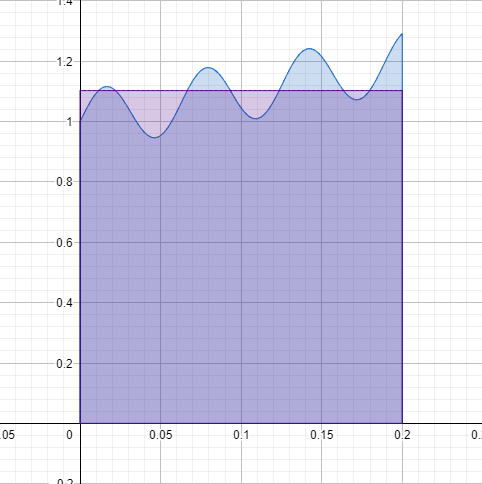
נדמיין שחיכינו לכך שמי הבריכה יהיו שקטים, וגובה המים יהיה קבוע. | |||
[[קובץ:calmpool.png| 800px]] | [[קובץ:calmpool.png| 800px]] | ||
נרצה להגדיר את גובה המים הממוצע בבריכה, כגובה המים כאשר פני הבריכה שקטים. | |||
מה משותף לבריכה כאשר היא גועשת וכאשר היא שקטה? כמות המים, כלומר '''השטח'''. | |||
אם כך, כאשר פני המים שקטים והבריכה בצורה מלבנית, הגובה הוא בדיוק השטח חלקי רוחב הבריכה. | |||
לכן נגדיר את גובה המים הממוצע באופן כללי כשטח המים חלקי רוחב הבריכה. | |||
===ניסוח מדוייק=== | |||
תהי f פונקציה רציפה בקטע <math>[a,b]</math>. נגדיר את '''הממוצע האינטגרלי''' של הפונקציה בקטע להיות | |||
:<math>\frac{\int_a^b f(x)dx}{b-a}</math> | |||
==משפט ערך הממוצע האינטגרלי== | |||
תהי f פונקציה רציפה בקטע <math>[a,b]</math>. אזי קיימת נקודה <math>c\in[a,b]</math> עבורה | |||
:<math>f(c)=\frac{\int_a^b f(x)dx}{b-a}</math> | |||
באנלוגיה שלנו, זה אומר שגובה הבריכה הממוצע חייב להיות גובה פני המים בנקודה כלשהי בבריכה. | |||
===הוכחה=== | |||
לפי [[חדוא 1 - ארז שיינר#משפטי ויירשטראס|משפט ווירשטראס]] הפונקציה f מקבלת מקסימום M ומינימום m בקטע. | |||
כלומר, לכל <math>x\in[a,b]</math> מתקיים כי <math>m\leq f(x)\leq M</math>. | |||
לכן | |||
:<math>m(b-a)\leq \int_a^b f(x)dx \leq M(b-a)</math> | |||
ומכאן | |||
:<math>m\leq \frac{\int_a^b f(x)dx}{b-a}\leq M</math> | |||
כלומר הממוצע האינטגרלי הוא ערך בין הגובה המינימלי של הפונקציה לגובה המקסימלי שלה בקטע. | |||
לסיום, לפי [[חדוא 1 - ארז שיינר#משפט ערך הביניים|משפט ערך הביניים]] נובע כי קיימת נקודה <math>c\in[a,b]</math> עבורה <math>f(c)=\frac{\int_a^b f(x)dx}{b-a}</math> | |||
גרסה אחרונה מ־18:58, 23 במרץ 2021
ממוצע אינטגרלי
כיצד הייתם מגדירים את גובה המים הממוצע בבריכה הבאה?
אמנם יש דרכים רבות להגדיר ממוצע, אך אנחנו נתאר דרך אחת.
נדמיין שחיכינו לכך שמי הבריכה יהיו שקטים, וגובה המים יהיה קבוע.
נרצה להגדיר את גובה המים הממוצע בבריכה, כגובה המים כאשר פני הבריכה שקטים.
מה משותף לבריכה כאשר היא גועשת וכאשר היא שקטה? כמות המים, כלומר השטח.
אם כך, כאשר פני המים שקטים והבריכה בצורה מלבנית, הגובה הוא בדיוק השטח חלקי רוחב הבריכה.
לכן נגדיר את גובה המים הממוצע באופן כללי כשטח המים חלקי רוחב הבריכה.
ניסוח מדוייק
תהי f פונקציה רציפה בקטע [math]\displaystyle{ [a,b] }[/math]. נגדיר את הממוצע האינטגרלי של הפונקציה בקטע להיות
- [math]\displaystyle{ \frac{\int_a^b f(x)dx}{b-a} }[/math]
משפט ערך הממוצע האינטגרלי
תהי f פונקציה רציפה בקטע [math]\displaystyle{ [a,b] }[/math]. אזי קיימת נקודה [math]\displaystyle{ c\in[a,b] }[/math] עבורה
- [math]\displaystyle{ f(c)=\frac{\int_a^b f(x)dx}{b-a} }[/math]
באנלוגיה שלנו, זה אומר שגובה הבריכה הממוצע חייב להיות גובה פני המים בנקודה כלשהי בבריכה.
הוכחה
לפי משפט ווירשטראס הפונקציה f מקבלת מקסימום M ומינימום m בקטע.
כלומר, לכל [math]\displaystyle{ x\in[a,b] }[/math] מתקיים כי [math]\displaystyle{ m\leq f(x)\leq M }[/math].
לכן
- [math]\displaystyle{ m(b-a)\leq \int_a^b f(x)dx \leq M(b-a) }[/math]
ומכאן
- [math]\displaystyle{ m\leq \frac{\int_a^b f(x)dx}{b-a}\leq M }[/math]
כלומר הממוצע האינטגרלי הוא ערך בין הגובה המינימלי של הפונקציה לגובה המקסימלי שלה בקטע.
לסיום, לפי משפט ערך הביניים נובע כי קיימת נקודה [math]\displaystyle{ c\in[a,b] }[/math] עבורה [math]\displaystyle{ f(c)=\frac{\int_a^b f(x)dx}{b-a} }[/math]