אי-שוויון הממוצעים

"נהוג לומר כי אם פותרים בעיה מסוימת אחת באופן מסוים אז זה תיחכום, ואם פותרים שתיים בעזרת אותו רעיון אז זו כבר שיטה."

(אסטרטגיות לפתרון בעיות מתמטיות, פרופ' בנו ארבל.)

אי־שוויון הממוצעים

יהיו מספרים חיוביים $0<a_1,\dots ,a_n\in \mathbb{R}$ אזי:

$\frac{n}{\frac{1}{a_1}+\cdots +\frac{1}{a_n}}\le \sqrt[n]{a_1\cdots a_n}\le \frac{a_1+\cdots +a_n}{n}$

כאשר משמאל מופיע הממוצע ההרמוני, במרכז הממוצע ההנדסי (גאומטרי) ומימין הממוצע החשבוני (אלגברי).

שיוויון מתקיים אם ורק אם כל המספרים שווים $a_1=\cdots =a_n$.

טענת עזר

ראשית, נוכיח את הטענה הבאה:

יהיו $x_1,\dots ,x_n$ ממשיים חיוביים המקיימים $x_1\cdots x_n=1$.

אזי $x_1+\cdots +x_n\ge n$, ושיוויון מתקיים אם ורק אם כולם שווים 1.

עבור n=1 הטענה טריוויאלית.

יהי n עבורו הטענה נכונה, ונוכיח אותה עבור n+1.

יהיו $x_1\le \cdots \le x_{n+1}$ ממשיים חיוביים המקיימים $x_1\cdots x_{n+1}=1$.

כיוון ש־$x_1$ הוא המספר הקטן ביותר, ואילו $x_{n+1}$ הוא המספר הגדול ביותר נובע כי $x_1\le 1$ ואילו $x_{n+1}\ge 1$.

נסמן $x_1\cdot x_{n+1}=y_n$, אזי $x_2\cdots x_n\cdot y_n=1$, ולפי הנחת האינדוקציה מתקיים כי $x_2+\cdots +x_n+y_n\ge n$ ושוויון אם"ם כולם שווים 1.

לכן אם נוכיח $x_1+\cdots +x_{n+1}\ge x_2+\cdots +x_n+x_1\cdot x_{n+1}+1$, נקבל $x_1+\cdots +x_{n+1}\ge n+1$.

כעת נוכיח את אי־השוויון הרצוי

$x_1+\cdots +x_{n+1}\ge x_2+\cdots +x_n+x_1\cdot x_{n+1}+1$.

זה נכון אם"ם

$x_1+x_{n+1}\ge x_1\cdot x_{n+1}+1$

זה שקול לאי־שוויון

$(x_1-1)(x_{n+1}-1)\le 0$

הוא נכון כיוון ש$x_1\le 1$ ואילו $x_{n+1}\ge 1$.

כעת שוויון $x_1+\cdots +x_{n+1}=n+1$ גורר כי $x_1+\cdots +x_{n+1}=x_2+\cdots +x_n+x_1\cdot x_{n+1}+1=n+1$ ולכן $(x_1-1)(x_{n+1}-1)=0$.

לכן $x_{n+1}=1$ או $x_1=1$.

אם $x_{n+1}=1$ כיוון שהוא הגדול מבין המספרים ומכפלתם היא 1, נובע כי $x_1=\cdots =x_n=1$. באופן דומה אם $x_1=1$ גם כל המספרים שווים 1.

הוכחת אי־שיוויון הממוצעים

נגדיר $x_i=\frac{a_i}{\sqrt[n]{a_1\cdots a_n}}$ ונבחין כי:

$x_1\cdots x_n=\frac{a_1}{\sqrt[n]{a_1\cdots a_n}}\cdots \frac{a_n}{\sqrt[n]{a_1\cdots a_n}}=1$

לכן לפי טענת העזר נקבל כי:

$x_1+\cdots +x_n=\frac{a_1+\cdots +a_n}{\sqrt[n]{a_1\cdots a_n}}\ge n$

ולכן $\sqrt[n]{a_1\cdots a_n}\le \frac{a_1+\cdots +a_n}{n}$ ושוויון אם"ם $x_1=\cdots =x_n=1$.

כלומר שוויון אם"ם $a_1=\cdots =a_n=\sqrt[n]{a_1\cdots a_n}$

כעת נציב את המספרים $\frac{1}{a_1},\dots ,\frac{1}{a_n}$ ונקבל כי:

$\sqrt[n]{\frac{1}{a_1}\cdots \frac{1}{a_n}}\le \frac{\frac{1}{a_1}+\cdots +\frac{1}{a_n}}{n}$

כלומר

$\frac{n}{\frac{1}{a_1}\cdots \frac{1}{a_n}}\le \sqrt[n]{a_1\cdots a_n}$

ושוויון אם"ם $\frac{1}{a_1}=\cdots =\frac{1}{a_n}$.

משמעות הממוצעים

נתון מלבן עם צלעות באורכים a,b. אנחנו רוצים למצוא 'ממוצע' של אורכי הצלעות, כלומר מספר אחד שיכול 'להחליף' את שניהם.

• אם חשוב לנו השטח, אנחנו בעצם מחפשים אורך x של צלע ריבוע ששטחו יהיה שווה לשטח המלבן. נקבל כמובן את הממוצע ההנדסי $x=\sqrt{ab}$.

• אם חשוב לנו ההיקף, אנחנו בעצם מחפשים אורך x של צלע ריבוע שהיקפו יהיה שווה להיקף המלבן. נקבל כמובן את הממוצע החשבוני $x=\frac{a+b}{2}$.

• ואם חשוב לנו השילוב בין השטח להיקף? בריבוע השטח חלקי ההיקף שווה לרבע הצלע. לכן אם רוצים לשמור על היחס בין השטח להיקף, אפשר לומר שהצלע 'הממוצעת' של המלבן היא 4 פעמים היחס בין השטח לבין ההיקף.

נקבל במקרה זה $x=4\cdot \frac{ab}{2(a+b)}=\frac{2ab}{a+b}=\frac{2}{\frac{1}{a}+\frac{1}{b}}$, הוא הממוצע ההרמוני.

נדגים את הממוצע ההרמוני בדרך נוספת:

נניח שהיום נסעתי לעבודה במהירות a וחזרתי הבייתה במהירות b (היו פקקים), כיצד נגדיר את המהירות הממוצעת של הנסיעה?

ובכן, מהירות * זמן = דרך. נסמן את המרחק בין ביתי לעבודה בx, לכן נסעתי בדרך לעבודה במשך זמן של $\frac{x}{a}$, וחזרתי בזמן של $\frac{x}{b}$.

אם כך, המהירות הכוללת של הדרך הכפולה שעברתי היא $\frac{2x}{\frac{x}{a}+\frac{x}{b}}$ וזה שוב הממוצע ההרמוני.

הערה: ניתן להכליל את כל הדוגמאות הללו עבור n מספרים.

שימושים

דוגמאות גאומטריות

היקפי מלבן וריבוע בעלי שטח זהה

יהיו מלבן וריבוע בעלי שטח זהה, אזי היקף המלבן גדול מהיקף הריבוע.

נסמן את שטח הצורות ב‏־s, ואת צלעות המלבן ב$a\ne b$.

אזי היקף המלבן הוא $2(a+b)$ ואילו היקף הריבוע הוא $4\sqrt{s}$.

לפי אי־שוויון הממוצעים נקבל כי:

$2(a+b)=4\frac{a+b}{2}>4\sqrt{ab}=4\sqrt{s}$

הכללה למקרה ה־n־ממדי

סכום הצלעות (פאות מממד 1) של תיבה תלת‏־ממדית היא $4(a+b+c)$ ומתקיים כי

$4(a+b+c)=12\cdot \frac{a+b+c}{3}>12\sqrt[3]{abc}$

ואילו $12\sqrt[3]{abc}$ הוא סכום הצלעות של הקוביה התלת־ממדית בעלת אותו השטח כמו התיבה.

כעת עבור תיבה n־ממדית, סכום הצלעות הוא $2^{n-1}(a_1+\cdots +a_n)$,

אכן, צלע היא המעבר בציר i מ־0 ל־$a_i$ כאשר כל שאר הצירים קבועים באחד הקצוות שלהם.

$2^{n-1}(a_1+\cdots +a_n)=n{2}^{n-1}\cdot \frac{a_1+\cdots +a_n}{n}>n{2}^{n-1}\cdot \sqrt[n]{a_1\cdots a_n}$

אורך הצלע של הקוביה ה־n־מימדית בעלת שטח זהה לתיבה הוא $\sqrt[n]{a_1\cdots a_n}$, וכמות הצלעות הינה $n{2}^{n-1}$.

לכן שוב קיבלנו שסכום הצלעות התיבה גדול מסכום צלעות הקוביה.

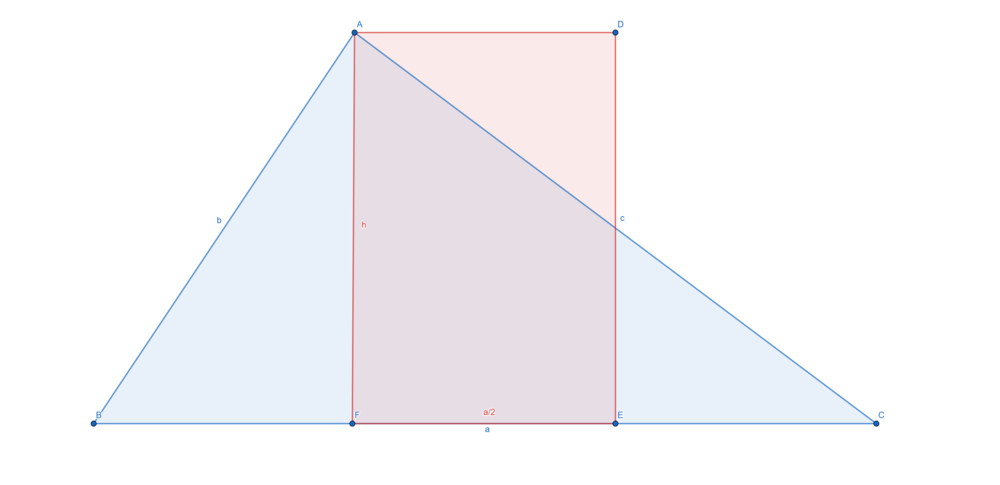
היקפי ריבוע ומשולש בעלי שטח זהה

יהיו משולש וריבוע בעלי שטח זהה, אזי היקף המשולש גדול מהיקף הריבוע.

נביט בבניית העזר הבאה:

(נבנה באמצעות גאוגברה.)

שטח המשולש זהה לשטח המלבן ושניהם שווים ל־$\frac{h\cdot a}{2}$.

היקף המשולש הוא $a+b+c$ והיקף המלבן $2(h+\frac{a}{2})=2h+a$, שהוא כאמור גדול מהיקף הריבוע (או שווה לו במקרה $h=\frac{a}{2}$).

כעת צלעות המשלוש גדולות או שווה לגובה, ולפחות אחת מהן גדולה ממש (במקרה שמדובר במשולש ישר זוית, הגובה שווה לאחת הצלעות).

$a+b+c>h+h+a=2h+a$

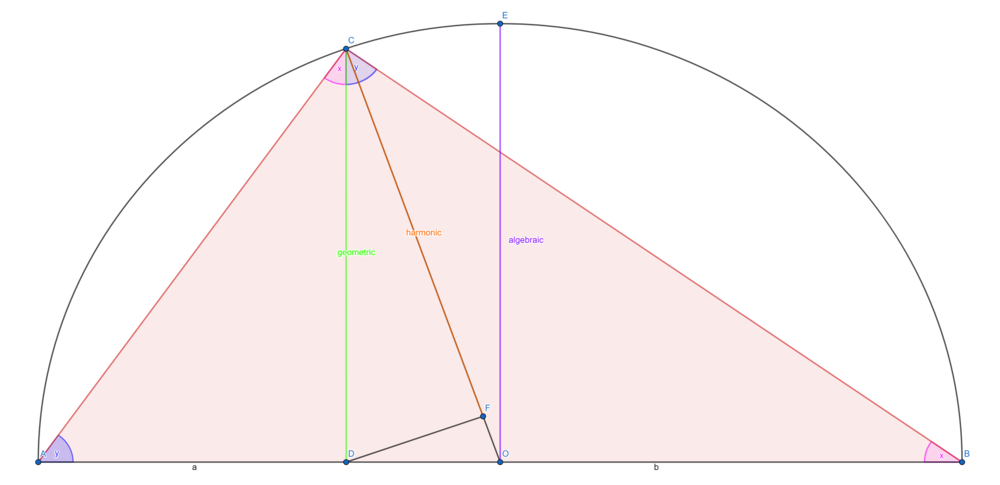
המחשה גאומטרית לשלושת הממוצעים עבור 2 מספרים

נביט בשרטוט הבא:

(נבנה באמצעות גאוגברה.)

נניח כי אורך הקטע AD הינו a ואורך הקטע DB הינו b.

הנקודה O הינה מרכז המעגל, שרדיוסו $\frac{a+b}{2}$ הרי הוא הממוצע החשבוני.

נרים את הגובה CD.

נשים לב כי הזוית C היא ישרה כיוון שהיא מונחת על הקוטר, ולכן המשולשים ADC ו CDB דומים.

מכאן $\frac{CD}{DB}=\frac{CD}{AD}$.

לכן $C{D}^2=a\cdot b$ וקיבלנו ש $CD=\sqrt{ab}$ הרי הוא הממוצע ההנדסי.

לבסוף, נעביר גובה DF, ונקבל כי המשולשים CFD ו CDO דומים.

לכן $\frac{CF}{CD}=\frac{CD}{CO}$

ולכן $CF=\frac{C{D}^2}{CO}=\frac{ab}{\frac{a+b}{2}}=\frac{2}{\frac{1}{a}+\frac{1}{b}}$ הרי הוא הממוצע ההרמוני.

משולש שווה צלעות

יהי משולש בעל צלעות באורך a,b,c.

הוכיחו כי המשולש שווה צלעות אם ורק אם $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=3$.

ראשית, $\sqrt[3]{\frac{a}{b}\cdot \frac{b}{c}\cdot \frac{c}{a}}\le \frac{\frac{a}{b}+\frac{b}{c}+\frac{c}{a}}{3}$ ושיוויון אם"ם כולם שווים.

לכן $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\ge 3$ ושיוויון רק אם $\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=1$, כלומר $a=b=c$

כלל המנה

תהי סדרה חיובית $0<a_n$ כך ש $\frac{a_{n+1}}{a_n}\to L$ אזי $\sqrt[n]{a_n}\to L$.

הממוצע החשבוני

תהי סדרה $a_n\to L$ אזי $\frac{a_1+...+a_n}{n}\to L$.

כלומר הממוצע החשבוני של סדרה מתכנסת במובן הרחב, מתכנס לאותו הגבול.

הוכחה עבור $L\in \mathbb{R}$:

יהי $\epsilon >0$.

קיים $n_1$ כך שלכל $n>n_1$ מתקיים כי $|a_n-L|<\frac{\epsilon }{2}$

נסמן $M=|a_1-L|+...+|a_{n_1}-L|$.

אזי $|\frac{a_1+...+a_n}{n}-L|=\left|\frac{(a_1-L)+...+(a_n-L)}{n}\right|\le \frac{M+(n-n_1)\frac{\epsilon }{2}}{n}\le \frac{M+n\frac{\epsilon }{2}}{n}$

נבחר $n_2>n_1$ כך שלכל $n>n_2$ מתקיים כי $\frac{M}{n}<\frac{\epsilon }{2}$.

סה"כ, לכל $n>n_2$ מתקיים כי $|\frac{a_1+...+a_n}{n}-L|<\epsilon$ כפי שרצינו.

הוכחה עבור $L=\mathrm{\infty }$:

יהי $M>0$.

קיים $n_1$ כך שלכל $n>n_1$ מתקיים כי $a_n>2M$.

נסמן $x=a_1+...+a_{n_1}$.

אזי $\frac{a_1+...+a_n}{n}>\frac{x+(n-n_1)2M}{n}=2M+\frac{x-n_1}{n}$

נבחר $n_2>n_1$ כך שלכל $n>n_2$ מתקיים כי $\frac{x-n_1}{n}>-M$

וביחד נקבל כי לכל $n>n_2$ מתקיים $\frac{a_1+...+a_n}{n}>M$

הממוצע ההרמוני

תהי סדרה $0<a_n\to L$ אזי $\frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to L$

כלומר הממוצע ההרמוני של סדרה מתכנסת במובן הרחב, מתכנס לאותו הגבול.

שימו לב שדרשנו שהסדרה חיובית, אחרת ייתכן צמצום שיוביל לאפס במכנה.

הוכחה עבור $0\ne L\in \mathbb{R}$:

$a_n\to L$, לכן $\frac{1}{a_n}\to \frac{1}{L}$.

לכן $\frac{\frac{1}{a_1}+...+\frac{1}{a_n}}{n}\to \frac{1}{L}$

ולכן $\frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to L$

הוכחה עבור $L=0$:

$\frac{1}{a_n}\to \mathrm{\infty }$

לכן $\frac{\frac{1}{a_1}+...+\frac{1}{a_n}}{n}\to \mathrm{\infty }$

ולכן $\frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to 0$

הוכחה עבור $L=\mathrm{\infty }$:

$\frac{1}{a_n}\to 0$

לכן $0<\frac{\frac{1}{a_1}+...+\frac{1}{a_n}}{n}\to 0$

ולכן $\frac{n}{\frac{1}{a_1}+...+\frac{1}{a_n}}\to \mathrm{\infty }$

הממוצע ההנדסי

לפי אי שיוויון הממוצעים, נובע כי אם $0<a_n\to L$ אזי $\sqrt[n]{a_1\cdots a_n}\to L$

הוכחת כלל המנה

תהי סדרה חיובית $0<a_n$ כך ש $\frac{a_{n+1}}{a_n}\to L$.

נגדיר את הסדרה $b_n$ ע"י $b_1=a_1$ ולכל $n>1$ מתקיים $b_n=\frac{a_n}{a_{n-1}}$

לכן הממוצע ההנדסי של הסדרה $b_n$ מקיים

$\sqrt[n]{a_1\cdot \frac{a_2}{a_1}\cdot \frac{a_3}{a_2}\cdots \frac{a_n}{a_{n-1}}}\to L$

לכן בעצם $\sqrt[n]{a_n}\to L$ כפי שרצינו.

המספר e

נוכיח כי הסדרה $a_n={(1+\frac{1}{n})}^n$ מונוטונית עולה ממש.

נחשב (סתם ככה בלי תירוצים נוספים) ממוצע הנדסי וחשבוני בין n+1 המספרים החיוביים הבאים (כי מותר, אז למה לא).

$x_1=(1+\frac{1}{n}),x_2=(1+\frac{1}{n}),...,x_n=(1+\frac{1}{n}),x_{n+1}=1$

לפי אי שיוויון הממוצעים (שהוא נכון תמיד, גם למספרים שבחרנו ככה באופן חסר אחריות), כיוון שלא מדובר במספרים שווים, הממוצע ההנדסי קטן ממש מהממוצע החשבוני:

$\sqrt[n+1]{{(1+\frac{1}{n})}^n}<\frac{(1+\frac{1}{n})+...+(1+\frac{1}{n})+1}{n+1}=\frac{n+2}{n+1}=1+\frac{1}{n+1}$

ולכן

${(1+\frac{1}{n})}^n<{(1+\frac{1}{n+1})}^{n+1}$

נוכיח כי הסדרה $b_n={(1+\frac{1}{n})}^{n+1}$ מונוטונית יורדת ממש.

באופן דומה, נשווה בין הממוצע ההרמוני לממוצע ההנדסי של n+2 המספרים הבאים:

$x_1=(1+\frac{1}{n}),x_2=(1+\frac{1}{n}),...,x_{n+1}=(1+\frac{1}{n}),x_{n+2}=1$

ונקבל:

$\sqrt[n+2]{{(1+\frac{1}{n})}^{n+1}}>\frac{n+2}{\frac{1}{(1+\frac{1}{n})}+...+\frac{1}{(1+\frac{1}{n})}+1}$

${(1+\frac{1}{n})}^{n+1}>{\left(\frac{n+2}{\frac{n+1}{1+\frac{1}{n}}+1}\right)}^{n+2}={\left(\frac{n+2}{\frac{n+1}{\frac{n+1}{n}}+1}\right)}^{n+2}={\left(\frac{n+2}{n+1}\right)}^{n+2}={(1+\frac{1}{n+1})}^{n+2}$

לכן סה"כ לכל $n$ מתקיים כי $a_1<a_n<b_n<b_1$ ושתי הסדרות מונוטוניות וחסומות ולכן מתכנסות.

נגדיר את המספר e להיות הגבול של הסדרה $a_n$.

לכן $b_n=a_n(1+\frac{1}{n})\to e\cdot 1=e$

ומתקיים לכל n כי $a_n<e<b_n$.

למשל עבור n=1 מקבלים כי $2<e<4$.

אי שיוויון ברנולי

יהי $ϵ>-1$, אזי לכל $n\in \mathbb{N}$ מתקיים כי ${(1+ϵ)}^n\ge 1+n\cdot ϵ$

אמנם לא מסובך במיוחד להוכיח את אי שיוויון ברנולי באינדוקציה, אנחנו נוכיח אותו באמצעות אי שיוויון הממוצעים.

למעשה באמצעות אי שיוויון הממוצעים, נוכיח גרסא רציונלית של אי השיוויון:

אם $\frac{m}{n}\ge 1$ אזי ${(1+ϵ)}^{\frac{m}{n}}\ge 1+\frac{m}{n}\cdot ϵ$

ראשית, אם $1+\frac{m}{n}\cdot ϵ<0$ אי השיוויון ברור.

לכן נניח כי $1+\frac{m}{n}\cdot ϵ\ge 0$.

לכן אי השיוויון שקול ל

$1+ϵ\ge \sqrt[m]{{(1+\frac{m}{n}ϵ)}^n}$

כעת

$\sqrt[m]{{(1+\frac{m}{n}ϵ)}^n\cdot 1^{m-n}}\le \frac{n\cdot (1+\frac{m}{n}ϵ)+(m-n)}{m}=1+ϵ$

שימוש באי שיוויון ברנולי

יהי $a>1$ אזי $a^n\to \mathrm{\infty }$.

נסמן $a=1+ϵ$, כאשר $ϵ>0$.

לכן $a^n=(1+ϵ{)}^n\ge 1+nϵ\to \mathrm{\infty }$.

יהי $0<a<1$ אזי $a^n\to 0$.

כיוון ש $0<a<1$ נובע כי $\frac{1}{a}>1$.

לכן, $a^n=\frac{1}{{\left(\frac{1}{a}\right)}^n}\to \frac{1}{\mathrm{\infty }}=0$

אי שיוויון קושי-שוורץ

עבור ${\mathbb{R}}^n$

לכל $a_1,...,a_n,b_1,...,b_n\in \mathbb{R}$ מתקיים

$|a_1{b}_1+...+a_n{b}_n|\le \sqrt{a_1^2+...+a_n^2}\sqrt{b_1^2+...+b_n^2}$

קל לראות שמספיק להוכיח את הטענה למספרים אי שליליים, וכך נעשה.

ראשית, אם נציב את $x^2,y^2$ באי שיוויון הממוצעים נקבל $xy\le \frac{x^2+y^2}{2}$.

לכן,

$\sum _{k=1}^n{x}_k{y}_k\le \frac{\sum _{k=1}^n{x}_k^2+\sum _{k=1}^n{y}_k^2}{2}$

כעת נציב $x_k=\frac{a_k}{\sqrt{a_1^2+...+a_n^2}}$ ו$y_k=\frac{b_k}{\sqrt{b_1^2+...+b_n^2}}$ לכל k ונקבל

$\frac{\sum _{k=1}^n{a}_k{b}_k}{\sqrt{a_1^2+...+a_n^2}\sqrt{b_1^2+...+b_n^2}}\le 1$

וזהו בדיוק אי שיוויון קושי שוורץ.

עבור מכפלה פנימית ממשית

האם אותה הוכחה מתרגמת עבור מכפלה פנימית ממשית כללית?

ובכן,

$⟨v-w,v-w⟩\ge 0$

ולכן

$⟨v,w⟩\le \frac{⟨v,v⟩+⟨w,w⟩}{2}$

שזה אנלוגי לאי שיוויון הממוצעים.

נציב את הנרמול של הוקטורים, ונקבל:

$⟨\frac{v}{||v||},\frac{w}{||w||}⟩\le 1$

ולכן $⟨v,w⟩\le ||v||\cdot ||w||$

ע"י הצבה של $-v$, נקבל

$-⟨v,w⟩\le ||v||\cdot ||w||$

וביחד סה"כ קיבלנו את אי שיוויון קושי-שוורץ:

$|⟨v,w⟩|\le ||v||\cdot ||w||$

עבור מכפלה פנימית מרוכבת

נתחיל מאי השיוויון

$⟨v-w,v-w⟩\ge 0$

אך הפעם נקבל

$Re(⟨v,w⟩)\le \frac{⟨v,v⟩+⟨w,w⟩}{2}$

על ידי הצבת הוקטורים המנורמלים נקבל את אי השיוויון החלש יותר:

$Re(⟨v,w⟩)\le ||v||\cdot ||w||$

נשים לב כי

$Re(⟨v,⟨v,w⟩w⟩)=Re(\overline{⟨v,w⟩}⟨v,w⟩)=|⟨v,w⟩{|}^2$

כיוון שהערך המוחלט הוא מספר ממשי.

לכן,

$|⟨v,w⟩{|}^2=Re(⟨v,⟨v,w⟩w⟩)\le ||v||\cdot ||⟨v,w⟩w||=||v||\cdot ||w||\cdot |⟨v,w⟩|$

ושוב קיבלנו את אי שיוויון קושי שוורץ, כפי שרצינו.

ביבליוגרפיה

• אסטרטגיות לפתרון בעיות מתמטיות, בנו ארבל.
• The Cauchy-Schwarz Master Class, J. Michael Steele.