88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 1.5: הבדלים בין גרסאות בדף
אחיה בר-און (שיחה | תרומות) |
אחיה בר-און (שיחה | תרומות) (←תרגיל) |
||
| (59 גרסאות ביניים של 7 משתמשים אינן מוצגות) | |||
| שורה 11: | שורה 11: | ||
בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור <math>n=1</math> כלומר <math>P(1)</math> מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור <math>n=1</math> (שזה אכן כך) אז הטענה נכונה גם עבור <math>n=2</math>כלומר <math>P(2)</math>. אה! אז עכשיו זה נכון עבור <math>n=2</math> אז לפי אותה טענה זה נכון גם עבור <math>n=3</math>! ומה עכשיו? אם זה נכון עבור <math>n=3</math> זה נכון עבור <math>n=4</math> . וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר <math>P(n)</math> נכון '''לכל''' <math>n</math> | בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור <math>n=1</math> כלומר <math>P(1)</math> מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור <math>n=1</math> (שזה אכן כך) אז הטענה נכונה גם עבור <math>n=2</math>כלומר <math>P(2)</math>. אה! אז עכשיו זה נכון עבור <math>n=2</math> אז לפי אותה טענה זה נכון גם עבור <math>n=3</math>! ומה עכשיו? אם זה נכון עבור <math>n=3</math> זה נכון עבור <math>n=4</math> . וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר <math>P(n)</math> נכון '''לכל''' <math>n</math> | ||
דוגמא | ====דוגמא==== | ||
נוכיח באינדוקציה כי הטענה <math>(1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3</math> | נוכיח באינדוקציה כי הטענה <math>(1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3</math> | ||
נכונה לכל <math>n\in \mathbb{N} </math> טבעי | נכונה לכל <math>n\in \mathbb{N} </math> טבעי | ||
| שורה 19: | שורה 19: | ||
עבור <math>n=1</math> אכן מתקיים כי <math>1^2=1^3</math> | עבור <math>n=1</math> אכן מתקיים כי <math>1^2=1^3</math> | ||
כעת | כעת נראה שאם הטענה נכונה עבור <math>n</math> כלשהוא, כלומר אם מתקיים | ||
<math>(1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3</math> | <math>(1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3</math> אזי הטענה נכונה עבור <math>n+1</math>, כלומר | ||
<math>(1+2+\cdots +n+n+1)^2 =1^3 +2^3 + \cdots +n^3 + (n+1)^3</math> | <math>(1+2+\cdots +n+(n+1))^2 =1^3 +2^3 + \cdots +n^3 + (n+1)^3</math>. כלומר נוכיח ש: <math>P(n) \to P(n+1)</math> | ||
נוכיח | נוכיח: | ||
<math>(1+2+\cdots +n+n+1)^2=(1+2+\cdots +n | <math>(1+2+\cdots +n+(n+1))^2=(1+2+\cdots +n)^2+2\cdot(1+2+\cdots +n)(n+1)+(n+1)^2 </math> | ||
לפי הנחת האינדוקציה אפשר להמשיך הלאה | לפי הנחת האינדוקציה אפשר להמשיך הלאה | ||
| שורה 36: | שורה 36: | ||
וסיימנו | וסיימנו | ||
== | ====דוגמא==== | ||
הוכח כי לכל מספר טבעי <math>n</math> מתקיים כי <math>2+4+6+\cdots +2n=n(n+1)</math> | |||
פתרון: | |||
עבור <math>n=1</math> אכן מתקיים <math>2=1\cdot(1+1)</math> | |||
כעת נניח שהטענה נכונה עבור <math>n</math> ונוכיח את הטענה עבור <math>n+1</math> | |||
<math>2+4+\cdots 2n+2(n+1)=\sum_{k=1}^{n+1}2\cdot k=\sum_{k=1}^{n}2\cdot k + 2(n+1) = </math> | |||
לפי הנחת האינדוקציה ניתן להמשיך | |||
<math>=n(n+1)+2(n+1)=(n+1)(n+2)</math> | |||
שזה הטענה עבור <math>n+1</math> וסיימנו. | |||
==== תרגיל ==== | |||
הוכיחו שלכל <math>n</math> טבעי מתקיים <math>\sum_{k=1}^{n}(2k-1)=n^{2}</math> | |||
=== לפעמים כדאי להניח הנחות חזקות יותר === | |||
תרגיל: | |||
נגדיר <math>a_0 =0 , a_{n+1}=a_n^2 +1/4</math>. | |||
הוכח כי לכל n מתקיים <math>a_n<1</math> | |||
פתרון: נוכיח משהו יותר חזק - לכל n מתקיים <math>a_n<1/2</math> | |||
אכן: עבור <math>a_0</math> זה מתקיים. כעת נניח שנכון עבור n ונראה עבור n+1 | |||
<math>a_{n+1}=a_n^2+1/4<(1/2)^2+1/4 =1/2</math> | |||
==הכללות== | ==הכללות== | ||
| שורה 57: | שורה 91: | ||
פתרון: | פתרון: | ||
עבור <math>n=2</math> נקבל <math>(1+x)^2 = 1+2x+x^2>1+2x</math> | עבור <math>n=2</math> נקבל <math>(1+x)^2 = 1+2x+x^2>1+2x</math>. | ||
כעת נניח כי הטענה נכונה עבור <math>n</math> כלשהוא, כלומר מתקיים <math>(1+x)^n > 1+nx</math> | כעת נניח כי הטענה נכונה עבור <math>n</math> כלשהוא, כלומר מתקיים <math>(1+x)^n > 1+nx</math> | ||
נוכיח עבור <math>n+1</math> מהנחת האינדוקציה נקבל כי | נוכיח עבור <math>n+1</math> מהנחת האינדוקציה נקבל כי | ||
<math> (1+x)^{n+1}=(1+x)^n\cdot (1+x)>(1+nx) +1+x > 1+x+nx =1+ (n+1)x </math> | <math> (1+x)^{n+1}=(1+x)^n\cdot (1+x)\stackrel{*}{>}(1+nx) (1+x)= 1+nx +x+nx^2 > 1+x+nx =1+ (n+1)x </math> | ||
כאשר המעבר <math>*</math> נובע מכך ש- <math>x>0</math>. | |||
וסיימנו | וסיימנו | ||
==== תרגיל ==== | |||
מצאו עבור אילו <math>n</math>ים מתקיים <math>n^{2}<2^{n}</math> | |||
===הכללה פשוטה 2 === | ===הכללה פשוטה 2 === | ||
| שורה 71: | שורה 110: | ||
* '''אם''' הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים <math>n</math> (כלומר מתקיים <math>P(m)</math> עבור <math>m\leq n</math>) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר <math>P(n+1)</math> מתקיים). | * '''אם''' הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים <math>n</math> (כלומר מתקיים <math>P(m)</math> עבור <math>m\leq n</math>) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר <math>P(n+1)</math> מתקיים). | ||
אז באופן דומה הטענה נכונה <math>P(n)</math> נכונה עבור <math>n\geq | אז באופן דומה הטענה נכונה <math>P(n)</math> נכונה עבור <math>n\geq 1</math> | ||
כלומר - אפשר להחליף את ההנחה שמתקיים עבור <math>n</math> ולהוכיח עבור <math>n+1</math> | כלומר - אפשר להחליף את ההנחה שמתקיים עבור <math>n</math> ולהוכיח עבור <math>n+1</math> | ||
| שורה 90: | שורה 129: | ||
אחרת <math>n+1</math> מתפרק למכפלה <math>n+1=ab</math> כאשר <math>1<a,b<n+1</math> | אחרת <math>n+1</math> מתפרק למכפלה <math>n+1=ab</math> כאשר <math>1<a,b<n+1</math> | ||
לפי הנחת האינדוקציה <math>a,b</math> מתפרקים למכפלה של מספרים ראשוניים | לפי הנחת האינדוקציה <math>a,b</math> מתפרקים למכפלה של מספרים ראשוניים | ||
<math>a=\Pi_{k=1}^l p_k,b=\Pi_{i=1}^r q_i</math> כאשר <math>p_k, | <math>a=\Pi_{k=1}^l p_k,b=\Pi_{i=1}^r q_i</math> כאשר <math>p_k,q_i</math> ראשוניים | ||
ואז <math>n=ab=\Pi_{k=1}^l p_k\cdot \Pi_{i=1}^r q_i</math> | ואז <math>n+1=ab=\Pi_{k=1}^l p_k\cdot \Pi_{i=1}^r q_i</math> | ||
וסיימנו | וסיימנו | ||
עוד תרגילים [[מכינה למתמטיקה קיץ תשעב/תרגילים/4]] | |||
[https://www.weizmann.ac.il/sci-tea/benari/sites/sci-tea.benari/files/uploads/softwareAndLearningMaterials/induction-he.pdf מדריך אינדוקציה של מכון ויצמן] | |||
== תרגילים יותר מעניינים (לא בסגנון "בני גורן". אם יש את הרקע המספק)== | |||
===תרגיל === | |||
יהא <math>A</math> פסוק. נגדיר בעזרת אינדוקציה פסוקים: | |||
<math>P_0 = A, P_n=(P_{n-1})\to A</math> | |||
הוכיחו כי <math>P_{n}</math> | |||
טואוטולוגיה כאשר <math>n</math> אי-זוגי. | |||
פתרון: נוכיח באינדוקציה כי לכל <math>n</math> אי-זוגי, הפסוק <math>P_{n}</math> | |||
הוא טואוטולוגיה.בדיקה: עבור <math>n=1</math>, הפסוק הוא <math>A\to A</math>. הוא אכן טואוטולוגיה. | |||
צעד: כעת, נניח את נכונות הטענה עבור <math>n</math> אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר <math>n+2</math>. | |||
מתקיים:<math>P_{n+2}=P_{n+1}\to A=(P_{n}\to A)\to A</math> נראה כי זו אכן טואוטולוגיה. ראשית, לפי ההנחה, <math>P_{n}\equiv T</math> | |||
לכל ערך של <math>A</math>. | |||
• אם <math>A=F</math>, נקבל <math>(T\to F)\to F\equiv F\to F</math>- אכן אמת. | |||
• אם <math>A=T</math>, נקבל <math> (T\to T)\to T\equiv T\to T</math> - אכן אמת. | |||
וסיימנו באינדוקציה. | |||
===תרגיל:=== | |||
יהיו <math>A_1,A_2,\dots A_n </math> קבוצות אזי <math>A_1 \triangle A_2 \triangle \dots \triangle A_n =\{x| x \; \; \text{in odd number of sets} \}</math> | |||
הוכחה: | |||
עבור <math>n=2</math> זה נכון כי הפרש סימטרי של 2 קבוצות זה כל ה <math>x</math> - ים שנמצאים או בראשונה בלבד או בשניה בלבד. | |||
נניח כי הטענה נכונה עבור <math>n</math> קבוצות. נוכיח עבור <math>n+1</math> קבוצות: | |||
<math>A_1 \triangle A_2 \triangle \dots \triangle A_n \triangle A_{n+1} = B\cup C </math> | |||
כאשר <math>B=\{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\backslash A_{n+1} \} = \{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \land x\not\in A_{n+1} \} | |||
, \; \\ C= \{ x \; | \; x \in A_{n+1} \backslash (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \} = \{x \; | \; x \in A_{n+1} \land x\not\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\}</math> | |||
לפי הנחת האינדוקציה מתקיים <math>A_1 \triangle A_2 \triangle \dots \triangle A_n =\{x| x \; \; \text{in odd number of sets from}\; A_1,A_2\dots A_n \}</math> ולכן ניתן להמשיך כך | |||
<math>B\cup C = \{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \; \land \; x\not\in A_{n+1}\} \cup \{x \; | \; x \in A_{n+1} \; \land \; x\not\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\} = </math> | |||
<math>\{x \; | \; x\in \; \text{in odd number of sets from}\; A_1,A_2\dots A_n \; \land \; x\not\in A_{n+1} \} \cup \{x \; | \; x \in A_{n+1} \; \land \; x\not\in \text{in odd number of sets from}\; A_1,A_2\dots A_n \} = </math> | |||
<math>\{x \; | x\not\in A_{n+1} \; \land \; x\in \; \text{in odd number of sets from}\; A_1,A_2\dots A_n \} \cup \{x \; | \; x \in A_{n+1} \; \land \; x \in \text{in even number of sets from}\; A_1,A_2\dots A_n \}=</math> | |||
<math>\{x \; | \; x\in \; \text{in odd number of sets from}\; A_1,A_2\dots A_n, A_{n+1} \}</math> | |||
לכן, הטענה נכונה גם עבור <math>n+1</math> וסיימנו | |||
=== תרגיל === | |||
יהא <math>a</math> מספר ממשי המקיים כי <math>a+\frac{1}{a}</math> מספר שלם. הוכיחו כי לכל <math>n</math> טבעי מתקיים כי <math>a^n+\frac{1}{a^n}</math> מספר שלם. | |||
=== תרגיל === | |||
לכל <math>n</math> טבעי מתקיים: כל טבלה ריבועית בגודל <math>2^{n}\times2^{n}</math> שהוצאנו ממנה משבצת, ניתן לכסות ב "י" (3 משבצות בצורת האות יוד) | |||
הוכחה: באינדוקציה. | |||
בסיס <math>n=1</math>: טבלה ריבועית בגודל 2 על 2, ואכן כל משבצת שנוציא נשאר עם צורה "יוד" בודדת. | |||
צעד: נניח נכונות עבור <math>n</math> ונוכיח נוכונות עבור <math>n+1</math>. תהא טבלה בגודל <math>2^{n+1}\times2^{n+1}</math> שהוצאנו משבצת. את הטבלה הזאת נחלק ל 4 טבלאות קטנות יותר בגודל <math>2^{n}\times2^{n}</math> שאחת מהן חסרה משבצת. את הטבלה הזאת ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה. בנוסף ניתן להוציא "יוד" נוספת כך ששלושת הטבלאות האחרות יהיו חסרות משבצת אחת בדיוק ואז גם אותם ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה. | |||
מסקנה: לכל <math>n</math> טבעי מתקיים ש 3 מחלק את <math>\left(2^{n}\right)^{2}-1</math>. | |||
=== תרגיל === | |||
תהא טבלת שוקולד עם <math>m</math> שורות ו <math>n</math> עמודות. חיתוך של טבלת שוקולד הוא שבירת הטבלה לשתי טבלאות קטנות לאורך או לרוחב הטבלה המקורית. הוכיחו כי בהינתן טבלה עם <math>N</math> קוביות שוקולד, צריך בדיוק <math>N-1</math> חיתוכים על מנת להפריד כל קוביה בנפרד (כלומר לקבל <math>N</math> טבלאות שכל אחת מגודל 1 על 1). | |||
הוכחה: באינדוקציה שלמה. אם הטבלה בגודל 1 על 1 סיימנו. אחרת, נבצע חיתוך שרירותי, נקבל 2 טבלאות קטנות יותר, נפעיל עליהם את הנחת האינדוקציה וסיימנו. | |||
===תרגיל=== | |||
הוכיחו בעזרת אינדוקציה כי כל מצולע קמור (כלומר הצלע בין כל שני קודקודים נמצאת בפנים המצולע) בן <math>n \geq 3</math> צלעות ניתן לשילוש (כלומר ניתן לחלק אותו למשולשים) | |||
ושיש בשילוש <math>n-3</math> אלכסונים. | |||
פתרון: | |||
עבור <math>n=3</math>: מצולע קמור בן 3 צלעות חייב להיות משולש (ייתכן בעיוות כלשהוא) ולכן הוא ניתן לשילוש ע"י | |||
<math>n-3=0</math> אלכסונים. | |||
כעת נניח שהטענה נכונה עבור כל מצולע קמור בן <math>3\leq k \leq n</math> ונוכיח את הטענה עבור מצלוע קמור בן <math>n+1</math> צלעות (כלומר שכל מצולע קמור בן <math>n+1</math> ניתן לשילוש עם <math>(n+1)-3</math> אלכסונים). יהא מצולע קמור <math>M</math> בן <math>n+1</math> צלעות. נמתח קו בין שני קודקודים שלו. כעת המצולע שהתחלנו איתו התחלק לשני מצולעים קמורים, נסמנם <math>M_1,M_2</math>. נסמן את מספר הצלעות של <math>M_1</math> ב <math>k</math> (כלומר יש לו <math>k-1</math> צלעות משותפות עם <math>M</math> + הצלע שהוספנו. מספר הצלעות של <math>M</math> הוא <math>n+1</math> ולכן מספר הצלעות המשותפות בין <math>M</math> ל <math>M_2</math> הוא | |||
<math>n+1-(k-1)=n-k+2</math> ולכן מספר הצלעות של <math>M_2</math> הוא <math>n-k+3</math>. | |||
כיוון ש <math>3\leq k,n-k+3\leq n+1</math> ניתן להפעיל את הנחת האינדוקציה על <math>M_1,M_2</math> ולהסיק כי <math>M_1,M_2</math> ניתן לשילוש ע"י <math>k-3,n-k+3 - 3</math> אלכסונים. | |||
צירוף השילושים של <math>M_1,M_2</math> יתן שילוש של <math>M</math> עם <math>(k-3) + (n-k)+1=(n+1)-3 </math> אלכסונים כנדרש. | |||
===תרגיל:=== | |||
יהיו <math>A_1,A_2\dots A_{m+1} \in \mathbb{F}^{n\times n}</math> מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י הנוסחא | |||
<math>(A_1A_2\cdots A_{m+1})_{i,j}=\underset{1\leq i_1,i_2,\dots i_m \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,j}</math> | |||
הוכחה (באינדוקציה על מספר המטריצות): | |||
עבור <math>m=1</math> זה ההגדרה של כפל בין 2 מטריצות | |||
כעת, נניח שהטענה נכונה עבור <math>m</math> כל שהוא. נוכיח נכונות עבור <math>m+1</math> | |||
<math>(A_1A_2\cdots A_{m+1}A_{m+2})_{i,j}=\sum_{i_{m+1}=1}^n (A_1A_2\cdots A_{m+1})_{i,i_{m+1}}(A_{m+2})_{i_{m+1},j}</math> | |||
לפי הנחת האינדוקציה נמשיך: | |||
<math>=\sum_{i_{m+1}=1}^n \underset{1\leq i_1,i_2,\dots i_m \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,i_{m+1}}(A_{m+2})_{i_{m+1},j} = </math> | |||
<math> = \underset{1\leq i_1,i_2,\dots i_m, i_{m+1} \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,i_{m+1}}(A_{m+2})_{i_{m+1},j}</math> | |||
וסיימנו. | |||
==אזהרה== | |||
אינדוקציה היא כלי חזק אך יש לשים לב כי משתמשים בו נכונה. | |||
דוגמא מפורסמת להוכחת שגויה באינדוקציה היא הדוגמא הבא: | |||
טענה: כל קבוצה של סוסים לא ריקה מכילה סוסים מצבע יחיד. | |||
"הוכחה": נוכיח בעזרת אינדוקציה על מספר האיברים בקבוצת הסוסים. | |||
עבור <math>n=1</math> אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד | |||
כעת נניח כל קבוצה עם <math>n</math> סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל <math>n+1</math> | |||
תהא <math>H=\{h_1,h_2,\dots h_n,h_{n+1}\}</math> קבוצה עם <math>n+1</math> סוסים אזי לפי הנחת האינדוקציה | |||
<math>H_1 =\{h_1,h_2,\dots h_n\}</math> ו <math>H_2=\{h_2,\dots h_n,h_{n+1}\}</math> הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל <math>n</math>) | |||
ולכן כל הסוסים ב <math>H</math> ג"כ בעלי צבע יחיד (כי יש חפיפה בין <math>H_1</math> ובין <math>H_2</math>. | |||
חישבו איפה השגיאה (רמז: במעבר מ <math>n=1</math> ל <math>n=2</math>) | |||
==סדר טוב - העשרה מתקדמת ביותר, לא להעביר לשנה א == | |||
הגדרה: יהי <math>R</math> יחס סדר חלקי על קבוצה <math>A</math>. | |||
<math>R</math> יקרא '''סדר טוב''' אם לכל <math>\emptyset \neq B\subseteq A</math> קיים איבר מינימום/הכי קטן/ראשון ב <math>B</math>. | |||
מינוח: נאמר כי <math>A</math> '''סדורה היטב'''. | |||
דוגמא: הקס"ח <math>(\{1,2,3\},\le)</math> היא סדורה היטב - תתי הקבוצות הלא ריקות שלה הן <math>\{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\},\{1,2,3\}</math> והאיבר הראשון בכל תת קבוצה הוא בהתאמה <math>1,2,3,1,2,1,1</math>. | |||
===עקרון הסדר הטוב=== | |||
נסתכל על <math>(\mathbb{N},\le)</math> - קבוצת הטבעיים עם יחס הסדר "קטן שווה" הסטנדרטי. | |||
אינטואיטיבית, אכן מתקיים כי לכל קבוצה לא ריקה של טבעיים קיים איבר ראשון - "אם 1 שם, הוא הקטן ביותר; אם 2 שם, הוא הקטן ביותר; ''ממשיכים כך'' עד שמגיעים לאיבר כלשהו (כי הקבוצה לא ריקה), והוא הקטן ביותר". | |||
פורמלית, טענה זו, הנקראת '''עקרון הסדר הטוב''', והיא '''שקולה''' לטענת (/אקסיומת) האינדוקציה. | |||
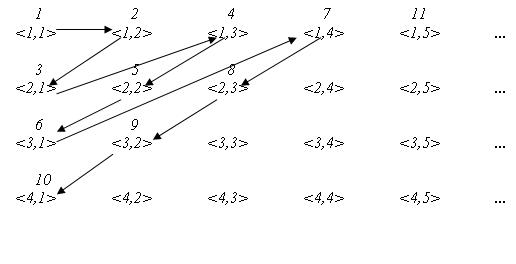
דוגמא נוספת: ניתן להגדיר אל <math>\mathbb{Q}_+</math> יחס סדר חלקי לפי התמונה הבא (כאשר מזהים כל שבר עם זוג סדור ומבטלים את החזרות המיותרות) | |||
[[קובץ:NutualSquareEqNutural.jpeg]] | |||
התבוננו והשתכנעו שזה גם סדר טוב. | |||
הערה: זה בניגוד לסדר "קטן שווה" הרגיל על השברים שאינו סדר טוב כי לקבוצה | |||
<math>\{x\in \mathbb{Q}_+ | \sqrt{2}<x \}</math> אין איבר מינימום. | |||
===משפט הסדר הטוב=== | |||
משפט הסדר הטוב קובע שלכל קבוצה <math>A</math> קיים סדר טוב. | |||
תרגיל: | |||
תהא <math>A</math> קבוצה בת מנייה. הוכח כי ניתן לסדר אותה היטב (בהינתן עקרון הסדר הטוב). | |||
פתרון: | |||
לפי הנתון קיימת פונקציה חח"ע ועל <math>f:A\to \mathbb{N} </math>. | |||
נגדיר את היחס הבא על <math>A</math> כך: <math>x\leq y \iff f(x)\leq f(y) </math>. זהו יחס סדר (השתכנעו!). | |||
בנוסף, <math>A</math> סדורה היטב על ידו: תהא <math>B\subseteq A</math> תת קבוצה לא ריקה. אזי <math>f(B)\subseteq\mathbb{N}</math> תת קבוצה לא ריקה ולכן קיים בה איבר מינימום נסמנו <math>n</math>. בדקו כי | |||
<math>f^{-1}(n)\in B</math> איבר מינימום. | |||
==== הכללה עקרון האינדוקציה בעזרת קבוצות סדורות היטב ==== | |||
תהא <math>A</math> קבוצה סדורה היטב (נסמן את היחס שלה ב<math>\leq</math>) אזי: | |||
* '''אם''' <math>\forall n ([\forall m<n P(m)] \to P(n))</math> | |||
*אז <math>P</math> מתקיימת לכל <math>a\in A</math> | |||
למה זה עובד? | |||
נניח בשלילה כי הטענה <math>P</math> לא מתקיימת לכל <math>a\in A</math> | |||
אזי נגדיר <math>D:=\{a\in A | P(a)=FALSE \}</math> - קבוצת כל האיברים ב <math>A</math> שעבורם הטענה אינה נכונה. מהנחת השלילה <math>D\neq \emptyset</math>. | |||
כיוון ש <math>A</math> סדורה היטב אזי קיים ב <math>D</math> מינימום, נסמנו <math>d</math>. לפי הגדרת מינימום והגדרת <math>D</math> נובע כי לכל <math>m<d</math> הטענה נכונה (אם היה <math>m<d</math> שהטענה לא נכונה לגביו אזי הוא היה בקבוצה <math>D</math> ואז זה היה סתירה לכך ש <math>d</math> מינימום של קבוצה זאת). | |||
אבל אם זה כך אז לפי הטענה שמוכיחים זה גורר כי <math>d</math> כן מתקיים. סתירה. ולכן הטענה נכונה לכל <math>a\in A</math> | |||
הערה: אפשר לעשות אינדוקציה הנקראת אינדוקציה טרנספניטית על קבוצות כלשהן (לאו דווקא בנות מניה) | |||
גרסה אחרונה מ־18:47, 6 ביולי 2022
רעיון בסיסי - אינדוקציה על הטבעיים
בשביל להוכיח שטענה מסוימת [math]\displaystyle{ P(n) }[/math] נכונה עבור כל מספר טבעי (למשל [math]\displaystyle{ (1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3 }[/math]) מספיק להוכיח את הבאים:
- (בסיס האינדוקציה) הטענה מתקיימת עבור [math]\displaystyle{ n=1 }[/math] כלומר [math]\displaystyle{ P(1) }[/math] מתקיים
- (צעד האינדוקציה)אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר [math]\displaystyle{ P(n)\Rightarrow P(n+1) }[/math].
למה זה מספיק? בוא נחשוב.. הוכחנו באופן ישיר כי הטענה נכונה עבור [math]\displaystyle{ n=1 }[/math] כלומר [math]\displaystyle{ P(1) }[/math] מתקיים. לכן לפי הטענה השניה, אם הטענה נכונה עבור [math]\displaystyle{ n=1 }[/math] (שזה אכן כך) אז הטענה נכונה גם עבור [math]\displaystyle{ n=2 }[/math]כלומר [math]\displaystyle{ P(2) }[/math]. אה! אז עכשיו זה נכון עבור [math]\displaystyle{ n=2 }[/math] אז לפי אותה טענה זה נכון גם עבור [math]\displaystyle{ n=3 }[/math]! ומה עכשיו? אם זה נכון עבור [math]\displaystyle{ n=3 }[/math] זה נכון עבור [math]\displaystyle{ n=4 }[/math] . וכן על זה הדרך. אפשר להשתכנע שבסופו של דבר [math]\displaystyle{ P(n) }[/math] נכון לכל [math]\displaystyle{ n }[/math]
דוגמא
נוכיח באינדוקציה כי הטענה [math]\displaystyle{ (1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3 }[/math] נכונה לכל [math]\displaystyle{ n\in \mathbb{N} }[/math] טבעי
הוכחה:
עבור [math]\displaystyle{ n=1 }[/math] אכן מתקיים כי [math]\displaystyle{ 1^2=1^3 }[/math]
כעת נראה שאם הטענה נכונה עבור [math]\displaystyle{ n }[/math] כלשהוא, כלומר אם מתקיים [math]\displaystyle{ (1+2+\cdots +n)^2 =1^3 +2^3 + \cdots +n^3 }[/math] אזי הטענה נכונה עבור [math]\displaystyle{ n+1 }[/math], כלומר [math]\displaystyle{ (1+2+\cdots +n+(n+1))^2 =1^3 +2^3 + \cdots +n^3 + (n+1)^3 }[/math]. כלומר נוכיח ש: [math]\displaystyle{ P(n) \to P(n+1) }[/math]
נוכיח:
[math]\displaystyle{ (1+2+\cdots +n+(n+1))^2=(1+2+\cdots +n)^2+2\cdot(1+2+\cdots +n)(n+1)+(n+1)^2 }[/math]
לפי הנחת האינדוקציה אפשר להמשיך הלאה
[math]\displaystyle{ =1^3 +2^3 + \cdots +n^3 +2\cdot (1+2+\cdots +n)(n+1)+(n+1)^2 }[/math] [math]\displaystyle{ =1^3 +2^3 + \cdots +n^3 +2 \cdot \frac{n(n+1)}{2}(n+1)+(n+1)^2 }[/math] [math]\displaystyle{ =1^3 +2^3 + \cdots +n^3 +n(n+1)^2+(n+1)^2 }[/math] [math]\displaystyle{ =1^3 +2^3 + \cdots +n^3 +(1+n)(n+1)^2=1^3 +2^3 + \cdots +n^3+(n+1)^3 }[/math]
וסיימנו
דוגמא
הוכח כי לכל מספר טבעי [math]\displaystyle{ n }[/math] מתקיים כי [math]\displaystyle{ 2+4+6+\cdots +2n=n(n+1) }[/math]
פתרון:
עבור [math]\displaystyle{ n=1 }[/math] אכן מתקיים [math]\displaystyle{ 2=1\cdot(1+1) }[/math]
כעת נניח שהטענה נכונה עבור [math]\displaystyle{ n }[/math] ונוכיח את הטענה עבור [math]\displaystyle{ n+1 }[/math]
[math]\displaystyle{ 2+4+\cdots 2n+2(n+1)=\sum_{k=1}^{n+1}2\cdot k=\sum_{k=1}^{n}2\cdot k + 2(n+1) = }[/math]
לפי הנחת האינדוקציה ניתן להמשיך
[math]\displaystyle{ =n(n+1)+2(n+1)=(n+1)(n+2) }[/math]
שזה הטענה עבור [math]\displaystyle{ n+1 }[/math] וסיימנו.
תרגיל
הוכיחו שלכל [math]\displaystyle{ n }[/math] טבעי מתקיים [math]\displaystyle{ \sum_{k=1}^{n}(2k-1)=n^{2} }[/math]
לפעמים כדאי להניח הנחות חזקות יותר
תרגיל:
נגדיר [math]\displaystyle{ a_0 =0 , a_{n+1}=a_n^2 +1/4 }[/math].
הוכח כי לכל n מתקיים [math]\displaystyle{ a_n\lt 1 }[/math]
פתרון: נוכיח משהו יותר חזק - לכל n מתקיים [math]\displaystyle{ a_n\lt 1/2 }[/math]
אכן: עבור [math]\displaystyle{ a_0 }[/math] זה מתקיים. כעת נניח שנכון עבור n ונראה עבור n+1
[math]\displaystyle{ a_{n+1}=a_n^2+1/4\lt (1/2)^2+1/4 =1/2 }[/math]
הכללות
הכללה פשוטה 1
הכללה ישירה מתבצעת כך (החלפה רק של הטענה הראשונה): אם נוכיח עבור טענה [math]\displaystyle{ P(n) }[/math] ש:
- הטענה מתקיימת עבור [math]\displaystyle{ n=k }[/math] מסוים כלומר [math]\displaystyle{ P(k) }[/math] מתקיים
- אם הטענה נכונה עבור מספר טבעי מסוים אזי היא נכונה גם עבור המספר הבא אחריו. כלומר [math]\displaystyle{ P(n)\Rightarrow P(n+1) }[/math].
אז באופן דומה הטענה נכונה [math]\displaystyle{ P(n) }[/math] נכונה עבור [math]\displaystyle{ n\geq k }[/math]
כלומר - במקום להוכיח עבור [math]\displaystyle{ n=1 }[/math] ואז הטענה מתקיים החל מ-1 ניתן להוכיח עבור [math]\displaystyle{ n=k }[/math] ואז הטענה מתקיים החל מ-k
דוגמא:
הוכח כי לכל [math]\displaystyle{ x\gt 0 }[/math] מתקיים [math]\displaystyle{ (1+x)^n \gt 1+nx }[/math] לכל [math]\displaystyle{ n\geq 2 }[/math]
פתרון:
עבור [math]\displaystyle{ n=2 }[/math] נקבל [math]\displaystyle{ (1+x)^2 = 1+2x+x^2\gt 1+2x }[/math].
כעת נניח כי הטענה נכונה עבור [math]\displaystyle{ n }[/math] כלשהוא, כלומר מתקיים [math]\displaystyle{ (1+x)^n \gt 1+nx }[/math]
נוכיח עבור [math]\displaystyle{ n+1 }[/math] מהנחת האינדוקציה נקבל כי [math]\displaystyle{ (1+x)^{n+1}=(1+x)^n\cdot (1+x)\stackrel{*}{\gt }(1+nx) (1+x)= 1+nx +x+nx^2 \gt 1+x+nx =1+ (n+1)x }[/math]
כאשר המעבר [math]\displaystyle{ * }[/math] נובע מכך ש- [math]\displaystyle{ x\gt 0 }[/math].
וסיימנו
תרגיל
מצאו עבור אילו [math]\displaystyle{ n }[/math]ים מתקיים [math]\displaystyle{ n^{2}\lt 2^{n} }[/math]
הכללה פשוטה 2
אם נוכיח עבור טענה [math]\displaystyle{ P(n) }[/math] ש:
- הטענה מתקיימת עבור [math]\displaystyle{ n=1 }[/math] מסוים כלומר [math]\displaystyle{ P(1) }[/math] מתקיים
- אם הטענה נכונה עבור כל המספרים עד מספר טבעי מסוים [math]\displaystyle{ n }[/math] (כלומר מתקיים [math]\displaystyle{ P(m) }[/math] עבור [math]\displaystyle{ m\leq n }[/math]) אזי היא נכונה גם עבור המספר הבא אחריו (כלומר [math]\displaystyle{ P(n+1) }[/math] מתקיים).
אז באופן דומה הטענה נכונה [math]\displaystyle{ P(n) }[/math] נכונה עבור [math]\displaystyle{ n\geq 1 }[/math]
כלומר - אפשר להחליף את ההנחה שמתקיים עבור [math]\displaystyle{ n }[/math] ולהוכיח עבור [math]\displaystyle{ n+1 }[/math] בהנחה שמתקיים עבור כל מי שקטן שווה [math]\displaystyle{ n }[/math] ולהוכיח עבור [math]\displaystyle{ n+1 }[/math]
דוגמא:
כל מספר טבעי [math]\displaystyle{ 1\lt n }[/math] ניתן להציגו כמכפלה של מספרים ראשוניים
הוכחה:
עבור [math]\displaystyle{ n=2 }[/math] זה נכון כי 2 ראשוני ואז הוא הפירוק של עצמו.
כעת נניח שהטענה נכונה לכל [math]\displaystyle{ 1\lt k\leq n }[/math] ונוכיח עבור [math]\displaystyle{ n+1 }[/math]
אם [math]\displaystyle{ n+1 }[/math] ראשוני - סיימנו כי אז הוא הפירוק של עצמו.
אחרת [math]\displaystyle{ n+1 }[/math] מתפרק למכפלה [math]\displaystyle{ n+1=ab }[/math] כאשר [math]\displaystyle{ 1\lt a,b\lt n+1 }[/math] לפי הנחת האינדוקציה [math]\displaystyle{ a,b }[/math] מתפרקים למכפלה של מספרים ראשוניים [math]\displaystyle{ a=\Pi_{k=1}^l p_k,b=\Pi_{i=1}^r q_i }[/math] כאשר [math]\displaystyle{ p_k,q_i }[/math] ראשוניים
ואז [math]\displaystyle{ n+1=ab=\Pi_{k=1}^l p_k\cdot \Pi_{i=1}^r q_i }[/math]
וסיימנו
עוד תרגילים מכינה למתמטיקה קיץ תשעב/תרגילים/4
מדריך אינדוקציה של מכון ויצמן
תרגילים יותר מעניינים (לא בסגנון "בני גורן". אם יש את הרקע המספק)
תרגיל
יהא [math]\displaystyle{ A }[/math] פסוק. נגדיר בעזרת אינדוקציה פסוקים: [math]\displaystyle{ P_0 = A, P_n=(P_{n-1})\to A }[/math] הוכיחו כי [math]\displaystyle{ P_{n} }[/math] טואוטולוגיה כאשר [math]\displaystyle{ n }[/math] אי-זוגי.
פתרון: נוכיח באינדוקציה כי לכל [math]\displaystyle{ n }[/math] אי-זוגי, הפסוק [math]\displaystyle{ P_{n} }[/math] הוא טואוטולוגיה.בדיקה: עבור [math]\displaystyle{ n=1 }[/math], הפסוק הוא [math]\displaystyle{ A\to A }[/math]. הוא אכן טואוטולוגיה.
צעד: כעת, נניח את נכונות הטענה עבור [math]\displaystyle{ n }[/math] אי-זוגי, ונוכיח עבור האי-זוגי הבא בתור, כלומר [math]\displaystyle{ n+2 }[/math].
מתקיים:[math]\displaystyle{ P_{n+2}=P_{n+1}\to A=(P_{n}\to A)\to A }[/math] נראה כי זו אכן טואוטולוגיה. ראשית, לפי ההנחה, [math]\displaystyle{ P_{n}\equiv T }[/math] לכל ערך של [math]\displaystyle{ A }[/math].
• אם [math]\displaystyle{ A=F }[/math], נקבל [math]\displaystyle{ (T\to F)\to F\equiv F\to F }[/math]- אכן אמת.
• אם [math]\displaystyle{ A=T }[/math], נקבל [math]\displaystyle{ (T\to T)\to T\equiv T\to T }[/math] - אכן אמת.
וסיימנו באינדוקציה.
תרגיל:
יהיו [math]\displaystyle{ A_1,A_2,\dots A_n }[/math] קבוצות אזי [math]\displaystyle{ A_1 \triangle A_2 \triangle \dots \triangle A_n =\{x| x \; \; \text{in odd number of sets} \} }[/math]
הוכחה:
עבור [math]\displaystyle{ n=2 }[/math] זה נכון כי הפרש סימטרי של 2 קבוצות זה כל ה [math]\displaystyle{ x }[/math] - ים שנמצאים או בראשונה בלבד או בשניה בלבד.
נניח כי הטענה נכונה עבור [math]\displaystyle{ n }[/math] קבוצות. נוכיח עבור [math]\displaystyle{ n+1 }[/math] קבוצות:
[math]\displaystyle{ A_1 \triangle A_2 \triangle \dots \triangle A_n \triangle A_{n+1} = B\cup C }[/math] כאשר [math]\displaystyle{ B=\{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\backslash A_{n+1} \} = \{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \land x\not\in A_{n+1} \} , \; \\ C= \{ x \; | \; x \in A_{n+1} \backslash (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \} = \{x \; | \; x \in A_{n+1} \land x\not\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\} }[/math]
לפי הנחת האינדוקציה מתקיים [math]\displaystyle{ A_1 \triangle A_2 \triangle \dots \triangle A_n =\{x| x \; \; \text{in odd number of sets from}\; A_1,A_2\dots A_n \} }[/math] ולכן ניתן להמשיך כך
[math]\displaystyle{ B\cup C = \{x \; | \; x\in (A_1 \triangle A_2 \triangle \dots \triangle A_n ) \; \land \; x\not\in A_{n+1}\} \cup \{x \; | \; x \in A_{n+1} \; \land \; x\not\in (A_1 \triangle A_2 \triangle \dots \triangle A_n )\} = }[/math]
[math]\displaystyle{ \{x \; | \; x\in \; \text{in odd number of sets from}\; A_1,A_2\dots A_n \; \land \; x\not\in A_{n+1} \} \cup \{x \; | \; x \in A_{n+1} \; \land \; x\not\in \text{in odd number of sets from}\; A_1,A_2\dots A_n \} = }[/math]
[math]\displaystyle{ \{x \; | x\not\in A_{n+1} \; \land \; x\in \; \text{in odd number of sets from}\; A_1,A_2\dots A_n \} \cup \{x \; | \; x \in A_{n+1} \; \land \; x \in \text{in even number of sets from}\; A_1,A_2\dots A_n \}= }[/math]
[math]\displaystyle{ \{x \; | \; x\in \; \text{in odd number of sets from}\; A_1,A_2\dots A_n, A_{n+1} \} }[/math]
לכן, הטענה נכונה גם עבור [math]\displaystyle{ n+1 }[/math] וסיימנו
תרגיל
יהא [math]\displaystyle{ a }[/math] מספר ממשי המקיים כי [math]\displaystyle{ a+\frac{1}{a} }[/math] מספר שלם. הוכיחו כי לכל [math]\displaystyle{ n }[/math] טבעי מתקיים כי [math]\displaystyle{ a^n+\frac{1}{a^n} }[/math] מספר שלם.
תרגיל
לכל [math]\displaystyle{ n }[/math] טבעי מתקיים: כל טבלה ריבועית בגודל [math]\displaystyle{ 2^{n}\times2^{n} }[/math] שהוצאנו ממנה משבצת, ניתן לכסות ב "י" (3 משבצות בצורת האות יוד)
הוכחה: באינדוקציה.
בסיס [math]\displaystyle{ n=1 }[/math]: טבלה ריבועית בגודל 2 על 2, ואכן כל משבצת שנוציא נשאר עם צורה "יוד" בודדת.
צעד: נניח נכונות עבור [math]\displaystyle{ n }[/math] ונוכיח נוכונות עבור [math]\displaystyle{ n+1 }[/math]. תהא טבלה בגודל [math]\displaystyle{ 2^{n+1}\times2^{n+1} }[/math] שהוצאנו משבצת. את הטבלה הזאת נחלק ל 4 טבלאות קטנות יותר בגודל [math]\displaystyle{ 2^{n}\times2^{n} }[/math] שאחת מהן חסרה משבצת. את הטבלה הזאת ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה. בנוסף ניתן להוציא "יוד" נוספת כך ששלושת הטבלאות האחרות יהיו חסרות משבצת אחת בדיוק ואז גם אותם ניתן לכסות ב"יוד" ים לפי הנחת האינדוקציה.
מסקנה: לכל [math]\displaystyle{ n }[/math] טבעי מתקיים ש 3 מחלק את [math]\displaystyle{ \left(2^{n}\right)^{2}-1 }[/math].
תרגיל
תהא טבלת שוקולד עם [math]\displaystyle{ m }[/math] שורות ו [math]\displaystyle{ n }[/math] עמודות. חיתוך של טבלת שוקולד הוא שבירת הטבלה לשתי טבלאות קטנות לאורך או לרוחב הטבלה המקורית. הוכיחו כי בהינתן טבלה עם [math]\displaystyle{ N }[/math] קוביות שוקולד, צריך בדיוק [math]\displaystyle{ N-1 }[/math] חיתוכים על מנת להפריד כל קוביה בנפרד (כלומר לקבל [math]\displaystyle{ N }[/math] טבלאות שכל אחת מגודל 1 על 1).
הוכחה: באינדוקציה שלמה. אם הטבלה בגודל 1 על 1 סיימנו. אחרת, נבצע חיתוך שרירותי, נקבל 2 טבלאות קטנות יותר, נפעיל עליהם את הנחת האינדוקציה וסיימנו.
תרגיל
הוכיחו בעזרת אינדוקציה כי כל מצולע קמור (כלומר הצלע בין כל שני קודקודים נמצאת בפנים המצולע) בן [math]\displaystyle{ n \geq 3 }[/math] צלעות ניתן לשילוש (כלומר ניתן לחלק אותו למשולשים) ושיש בשילוש [math]\displaystyle{ n-3 }[/math] אלכסונים.
פתרון: עבור [math]\displaystyle{ n=3 }[/math]: מצולע קמור בן 3 צלעות חייב להיות משולש (ייתכן בעיוות כלשהוא) ולכן הוא ניתן לשילוש ע"י [math]\displaystyle{ n-3=0 }[/math] אלכסונים.
כעת נניח שהטענה נכונה עבור כל מצולע קמור בן [math]\displaystyle{ 3\leq k \leq n }[/math] ונוכיח את הטענה עבור מצלוע קמור בן [math]\displaystyle{ n+1 }[/math] צלעות (כלומר שכל מצולע קמור בן [math]\displaystyle{ n+1 }[/math] ניתן לשילוש עם [math]\displaystyle{ (n+1)-3 }[/math] אלכסונים). יהא מצולע קמור [math]\displaystyle{ M }[/math] בן [math]\displaystyle{ n+1 }[/math] צלעות. נמתח קו בין שני קודקודים שלו. כעת המצולע שהתחלנו איתו התחלק לשני מצולעים קמורים, נסמנם [math]\displaystyle{ M_1,M_2 }[/math]. נסמן את מספר הצלעות של [math]\displaystyle{ M_1 }[/math] ב [math]\displaystyle{ k }[/math] (כלומר יש לו [math]\displaystyle{ k-1 }[/math] צלעות משותפות עם [math]\displaystyle{ M }[/math] + הצלע שהוספנו. מספר הצלעות של [math]\displaystyle{ M }[/math] הוא [math]\displaystyle{ n+1 }[/math] ולכן מספר הצלעות המשותפות בין [math]\displaystyle{ M }[/math] ל [math]\displaystyle{ M_2 }[/math] הוא [math]\displaystyle{ n+1-(k-1)=n-k+2 }[/math] ולכן מספר הצלעות של [math]\displaystyle{ M_2 }[/math] הוא [math]\displaystyle{ n-k+3 }[/math]. כיוון ש [math]\displaystyle{ 3\leq k,n-k+3\leq n+1 }[/math] ניתן להפעיל את הנחת האינדוקציה על [math]\displaystyle{ M_1,M_2 }[/math] ולהסיק כי [math]\displaystyle{ M_1,M_2 }[/math] ניתן לשילוש ע"י [math]\displaystyle{ k-3,n-k+3 - 3 }[/math] אלכסונים. צירוף השילושים של [math]\displaystyle{ M_1,M_2 }[/math] יתן שילוש של [math]\displaystyle{ M }[/math] עם [math]\displaystyle{ (k-3) + (n-k)+1=(n+1)-3 }[/math] אלכסונים כנדרש.
תרגיל:
יהיו [math]\displaystyle{ A_1,A_2\dots A_{m+1} \in \mathbb{F}^{n\times n} }[/math] מטריצות ריבועיות אזי האיבר הכללי של המכפלה של כולם ניתן ע"י הנוסחא [math]\displaystyle{ (A_1A_2\cdots A_{m+1})_{i,j}=\underset{1\leq i_1,i_2,\dots i_m \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,j} }[/math]
הוכחה (באינדוקציה על מספר המטריצות):
עבור [math]\displaystyle{ m=1 }[/math] זה ההגדרה של כפל בין 2 מטריצות
כעת, נניח שהטענה נכונה עבור [math]\displaystyle{ m }[/math] כל שהוא. נוכיח נכונות עבור [math]\displaystyle{ m+1 }[/math]
[math]\displaystyle{ (A_1A_2\cdots A_{m+1}A_{m+2})_{i,j}=\sum_{i_{m+1}=1}^n (A_1A_2\cdots A_{m+1})_{i,i_{m+1}}(A_{m+2})_{i_{m+1},j} }[/math]
לפי הנחת האינדוקציה נמשיך:
[math]\displaystyle{ =\sum_{i_{m+1}=1}^n \underset{1\leq i_1,i_2,\dots i_m \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,i_{m+1}}(A_{m+2})_{i_{m+1},j} = }[/math]
[math]\displaystyle{ = \underset{1\leq i_1,i_2,\dots i_m, i_{m+1} \leq n}{\sum}(A_1)_{i,i_1}(A_2)_{i_1,i_2}\dots (A_{m+1})_{i_m,i_{m+1}}(A_{m+2})_{i_{m+1},j} }[/math]
וסיימנו.
אזהרה
אינדוקציה היא כלי חזק אך יש לשים לב כי משתמשים בו נכונה.
דוגמא מפורסמת להוכחת שגויה באינדוקציה היא הדוגמא הבא:
טענה: כל קבוצה של סוסים לא ריקה מכילה סוסים מצבע יחיד.
"הוכחה": נוכיח בעזרת אינדוקציה על מספר האיברים בקבוצת הסוסים.
עבור [math]\displaystyle{ n=1 }[/math] אכן מתקיים כי קבוצה עם סוס אחד מכילה רק סוסים מצבע יחיד
כעת נניח כל קבוצה עם [math]\displaystyle{ n }[/math] סוסים מכילה סוסים רק מצבע יחיד ונוכיח את הטענה לקבוצת סוסים מגודל [math]\displaystyle{ n+1 }[/math]
תהא [math]\displaystyle{ H=\{h_1,h_2,\dots h_n,h_{n+1}\} }[/math] קבוצה עם [math]\displaystyle{ n+1 }[/math] סוסים אזי לפי הנחת האינדוקציה [math]\displaystyle{ H_1 =\{h_1,h_2,\dots h_n\} }[/math] ו [math]\displaystyle{ H_2=\{h_2,\dots h_n,h_{n+1}\} }[/math] הן קבוצות שמכילות סוסים מצבע יחיד (כי אלו קבוצות סוסים מגודל [math]\displaystyle{ n }[/math]) ולכן כל הסוסים ב [math]\displaystyle{ H }[/math] ג"כ בעלי צבע יחיד (כי יש חפיפה בין [math]\displaystyle{ H_1 }[/math] ובין [math]\displaystyle{ H_2 }[/math].
חישבו איפה השגיאה (רמז: במעבר מ [math]\displaystyle{ n=1 }[/math] ל [math]\displaystyle{ n=2 }[/math])
סדר טוב - העשרה מתקדמת ביותר, לא להעביר לשנה א
הגדרה: יהי [math]\displaystyle{ R }[/math] יחס סדר חלקי על קבוצה [math]\displaystyle{ A }[/math].
[math]\displaystyle{ R }[/math] יקרא סדר טוב אם לכל [math]\displaystyle{ \emptyset \neq B\subseteq A }[/math] קיים איבר מינימום/הכי קטן/ראשון ב [math]\displaystyle{ B }[/math].
מינוח: נאמר כי [math]\displaystyle{ A }[/math] סדורה היטב.
דוגמא: הקס"ח [math]\displaystyle{ (\{1,2,3\},\le) }[/math] היא סדורה היטב - תתי הקבוצות הלא ריקות שלה הן [math]\displaystyle{ \{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\},\{1,2,3\} }[/math] והאיבר הראשון בכל תת קבוצה הוא בהתאמה [math]\displaystyle{ 1,2,3,1,2,1,1 }[/math].
עקרון הסדר הטוב
נסתכל על [math]\displaystyle{ (\mathbb{N},\le) }[/math] - קבוצת הטבעיים עם יחס הסדר "קטן שווה" הסטנדרטי.
אינטואיטיבית, אכן מתקיים כי לכל קבוצה לא ריקה של טבעיים קיים איבר ראשון - "אם 1 שם, הוא הקטן ביותר; אם 2 שם, הוא הקטן ביותר; ממשיכים כך עד שמגיעים לאיבר כלשהו (כי הקבוצה לא ריקה), והוא הקטן ביותר".
פורמלית, טענה זו, הנקראת עקרון הסדר הטוב, והיא שקולה לטענת (/אקסיומת) האינדוקציה.
דוגמא נוספת: ניתן להגדיר אל [math]\displaystyle{ \mathbb{Q}_+ }[/math] יחס סדר חלקי לפי התמונה הבא (כאשר מזהים כל שבר עם זוג סדור ומבטלים את החזרות המיותרות)
התבוננו והשתכנעו שזה גם סדר טוב.
הערה: זה בניגוד לסדר "קטן שווה" הרגיל על השברים שאינו סדר טוב כי לקבוצה [math]\displaystyle{ \{x\in \mathbb{Q}_+ | \sqrt{2}\lt x \} }[/math] אין איבר מינימום.
משפט הסדר הטוב
משפט הסדר הטוב קובע שלכל קבוצה [math]\displaystyle{ A }[/math] קיים סדר טוב.
תרגיל:
תהא [math]\displaystyle{ A }[/math] קבוצה בת מנייה. הוכח כי ניתן לסדר אותה היטב (בהינתן עקרון הסדר הטוב).
פתרון:
לפי הנתון קיימת פונקציה חח"ע ועל [math]\displaystyle{ f:A\to \mathbb{N} }[/math]. נגדיר את היחס הבא על [math]\displaystyle{ A }[/math] כך: [math]\displaystyle{ x\leq y \iff f(x)\leq f(y) }[/math]. זהו יחס סדר (השתכנעו!). בנוסף, [math]\displaystyle{ A }[/math] סדורה היטב על ידו: תהא [math]\displaystyle{ B\subseteq A }[/math] תת קבוצה לא ריקה. אזי [math]\displaystyle{ f(B)\subseteq\mathbb{N} }[/math] תת קבוצה לא ריקה ולכן קיים בה איבר מינימום נסמנו [math]\displaystyle{ n }[/math]. בדקו כי [math]\displaystyle{ f^{-1}(n)\in B }[/math] איבר מינימום.
הכללה עקרון האינדוקציה בעזרת קבוצות סדורות היטב
תהא [math]\displaystyle{ A }[/math] קבוצה סדורה היטב (נסמן את היחס שלה ב[math]\displaystyle{ \leq }[/math]) אזי:
- אם [math]\displaystyle{ \forall n ([\forall m\lt n P(m)] \to P(n)) }[/math]
- אז [math]\displaystyle{ P }[/math] מתקיימת לכל [math]\displaystyle{ a\in A }[/math]
למה זה עובד?
נניח בשלילה כי הטענה [math]\displaystyle{ P }[/math] לא מתקיימת לכל [math]\displaystyle{ a\in A }[/math] אזי נגדיר [math]\displaystyle{ D:=\{a\in A | P(a)=FALSE \} }[/math] - קבוצת כל האיברים ב [math]\displaystyle{ A }[/math] שעבורם הטענה אינה נכונה. מהנחת השלילה [math]\displaystyle{ D\neq \emptyset }[/math].
כיוון ש [math]\displaystyle{ A }[/math] סדורה היטב אזי קיים ב [math]\displaystyle{ D }[/math] מינימום, נסמנו [math]\displaystyle{ d }[/math]. לפי הגדרת מינימום והגדרת [math]\displaystyle{ D }[/math] נובע כי לכל [math]\displaystyle{ m\lt d }[/math] הטענה נכונה (אם היה [math]\displaystyle{ m\lt d }[/math] שהטענה לא נכונה לגביו אזי הוא היה בקבוצה [math]\displaystyle{ D }[/math] ואז זה היה סתירה לכך ש [math]\displaystyle{ d }[/math] מינימום של קבוצה זאת).
אבל אם זה כך אז לפי הטענה שמוכיחים זה גורר כי [math]\displaystyle{ d }[/math] כן מתקיים. סתירה. ולכן הטענה נכונה לכל [math]\displaystyle{ a\in A }[/math]
הערה: אפשר לעשות אינדוקציה הנקראת אינדוקציה טרנספניטית על קבוצות כלשהן (לאו דווקא בנות מניה)