(יצירת דף עם התוכן "'''הומומורפיזם של חבורות''' הוא פונקציה מחבורה אחת לשניה, השומרת על הפעולה. '''ניסוח פורמ...") |
|||
| (גרסת ביניים אחת של אותו משתמש אינה מוצגת) | |||
| שורה 18: | שורה 18: | ||
3. האמור לעיל ב-1 ו-2 מותנה בכך שהחבורה "השניה" ניתנת לבחירה חופשית. למשל, אין זה נכון שלכל תת-חבורה H_0 של חבורה H קיים הומומורפיזם *מ-H* ל-H שתמונתו H_0; ואין זה נכון שלכל תת-חבורה נורמלית G_0 של חבורה G קיים הומומורפיזם מ-G *ל-G* שגרעינו G_0. | 3. האמור לעיל ב-1 ו-2 מותנה בכך שהחבורה "השניה" ניתנת לבחירה חופשית. למשל, אין זה נכון שלכל תת-חבורה H_0 של חבורה H קיים הומומורפיזם *מ-H* ל-H שתמונתו H_0; ואין זה נכון שלכל תת-חבורה נורמלית G_0 של חבורה G קיים הומומורפיזם מ-G *ל-G* שגרעינו G_0. | ||
| + | |||
| + | == הומומורפיזם וסדר של אברים == | ||
| + | |||
| + | כל הומומורפיזם מקיים <math>\ \varphi(x^n) = \varphi(x)^n</math>. לכן, אם ה[[סדר של איבר|סדר]] של x מחלק את n, אז גם הסדר של התמונה שלו מחלקת את n. בפרט, הסדר של <math>\ \varphi(x)</math> מחלק את הסדר של x. | ||
| + | |||
| + | לעומת זאת, מונומורפיזם (כלומר, הומומורפיזם חד-חד-ערכי) שומר על הסדר. | ||
== תאור הומומורפיזמים == | == תאור הומומורפיזמים == | ||
| שורה 29: | שורה 35: | ||
תהי <math>\ \{g_1,\dots,g_m\}</math> קבוצת יוצרים של חבורה G, ותהי H חבורה כלשהי. כל הומומורפיזם <math>\ f : G \rightarrow H</math> נקבע על-ידי התמונות <math>\ f(g_1),\dots,f(g_m)</math>. מאידך, לא כל בחירה של התמונות מגדירה הומומורפיזם! לתאור מלא של התופעה ראו [[יוצרים ויחסים]]. | תהי <math>\ \{g_1,\dots,g_m\}</math> קבוצת יוצרים של חבורה G, ותהי H חבורה כלשהי. כל הומומורפיזם <math>\ f : G \rightarrow H</math> נקבע על-ידי התמונות <math>\ f(g_1),\dots,f(g_m)</math>. מאידך, לא כל בחירה של התמונות מגדירה הומומורפיזם! לתאור מלא של התופעה ראו [[יוצרים ויחסים]]. | ||
| + | |||
| + | '''תרגיל''' (89214 תשע"ב מועד א'). כמה הומומורפיזמים יש מה[[חבורה ציקלית|חבורה הציקלית]] <math>\ \mathbb{Z}_{12}</math> ל[[חבורה סימטרית|חבורה הסימטרית]] <math>\ S_5</math>? | ||
| + | |||
| + | '''פתרון'''. הומומורפיזם f כזה נקבע על-ידי תמונת האיבר 1, אבל התמונה מקיימת <math>\ \operatorname{id} = f(0) = f(12) = f(1)^{12}</math>, ולכן היא מסדר המחלק את 12. בחבורה <math>\ S_5</math> יש רק [[מחלקת צמידות]] אחת שהסדר של אברים בה אינו מחלק את 12, ובה 24 אברים; לכן מספר ההומומורפיזמים הוא 120-24=96. | ||
[[קטגוריה:89214]] | [[קטגוריה:89214]] | ||
גרסה אחרונה מ־19:10, 15 בפברואר 2012
הומומורפיזם של חבורות הוא פונקציה מחבורה אחת לשניה, השומרת על הפעולה.
ניסוח פורמלי. תהיינה G,H חבורות. הומומורפיזם מ-G ל-H הוא פונקציה 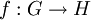 , המקיימת
, המקיימת 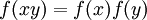 לכל
לכל 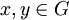 . בשוויון זה, הפעולה משמאל היא הפעולה של G, ואילו הפעולה מימין היא פעולת H.
. בשוויון זה, הפעולה משמאל היא הפעולה של G, ואילו הפעולה מימין היא פעולת H.
להומומורפיזמים המקיימים תכונות נוספות יש שמות מיוחדים: הומומורפיזם חד-חד-ערכי הוא מונומורפיזם; הומומורפיזם על הוא אפימורפיזם; הומומורפיזם שהוא גם חד-חד-ערכי וגם על הוא איזומורפיזם. הומומורפיזם מחבורה לעצמה נקרא אנדומורפיזם, ואיזומורפיזם מחבורה לעצמה נקרא אוטומורפיזם.
התמונה והגרעין
לכל הומומורפיזם 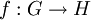 אפשר להגדיר תמונה וגרעין. התמונה היא תת-חבורה של הטווח H. הגרעין הוא תת-חבורה נורמלית של המקור G.
אפשר להגדיר תמונה וגרעין. התמונה היא תת-חבורה של הטווח H. הגרעין הוא תת-חבורה נורמלית של המקור G.
- משפט האיזומורפיזם הראשון מתרגם הומומורפיזמים לאיזומורפיזמים: לכל הומומורפיזם
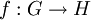 , חבורת המנה
, חבורת המנה 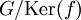 איזומורפית לתמונה של f.
איזומורפית לתמונה של f.
דגשים
1. כאמור לעיל, התמונה של הומומורפיזם מ-G ל-H היא תת-חבורה של H. לתמונה, ככלל, אין תכונות נוספות. כלומר, בהנתן חבורה H ותת-חבורה שלה H_0, תמיד קיים הומומורפיזם מחבורה כלשהי אל H, שתמונתו היא בדיוק H_0.
2. הגרעין של הומומורפיזם מחבורה G לחבורה כלשהי, הוא תת-חבורה נורמלית של G. גם כאן, לכל חבורה G ותת-חבורה נורמלית שלה, G_0, יש הומומורפיזם מ-G לחבורה מתאימה, שגרעינו שווה בדיוק ל-G_0.
3. האמור לעיל ב-1 ו-2 מותנה בכך שהחבורה "השניה" ניתנת לבחירה חופשית. למשל, אין זה נכון שלכל תת-חבורה H_0 של חבורה H קיים הומומורפיזם *מ-H* ל-H שתמונתו H_0; ואין זה נכון שלכל תת-חבורה נורמלית G_0 של חבורה G קיים הומומורפיזם מ-G *ל-G* שגרעינו G_0.
הומומורפיזם וסדר של אברים
כל הומומורפיזם מקיים 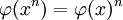 . לכן, אם הסדר של x מחלק את n, אז גם הסדר של התמונה שלו מחלקת את n. בפרט, הסדר של
. לכן, אם הסדר של x מחלק את n, אז גם הסדר של התמונה שלו מחלקת את n. בפרט, הסדר של 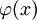 מחלק את הסדר של x.
מחלק את הסדר של x.
לעומת זאת, מונומורפיזם (כלומר, הומומורפיזם חד-חד-ערכי) שומר על הסדר.
תאור הומומורפיזמים
אם שני הומומורפיזמים מחבורה G (לחבורה כלשהי) מסכימים על קבוצת יוצרים, אז הם שווים. מכאן שכדי לתאר הומומורפיזם, די לקבוע לאן הוא שולח קבוצת יוצרים S של החבורה. הסיבה היא שכל איבר בחבורה אפשר להציג כמכפלה של אברי S, ואם 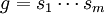 אז לכל הומומורפיזם
אז לכל הומומורפיזם 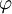 מ-G,
מ-G, 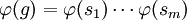 ולכן אפשר לחשב את
ולכן אפשר לחשב את 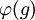 מידיעת
מידיעת
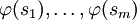 .
.
דגשים
בתאור הומומורפיזם, די לתאר אותו על קבוצת יוצרים כלשהי. לחבורה יכולות להיות קבוצות יוצרים רבות: אין שום צורך להגדיר את ההומומורפיזם על כולן.
תהי 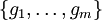 קבוצת יוצרים של חבורה G, ותהי H חבורה כלשהי. כל הומומורפיזם
קבוצת יוצרים של חבורה G, ותהי H חבורה כלשהי. כל הומומורפיזם 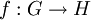 נקבע על-ידי התמונות
נקבע על-ידי התמונות 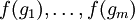 . מאידך, לא כל בחירה של התמונות מגדירה הומומורפיזם! לתאור מלא של התופעה ראו יוצרים ויחסים.
. מאידך, לא כל בחירה של התמונות מגדירה הומומורפיזם! לתאור מלא של התופעה ראו יוצרים ויחסים.
תרגיל (89214 תשע"ב מועד א'). כמה הומומורפיזמים יש מהחבורה הציקלית 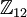 לחבורה הסימטרית
לחבורה הסימטרית 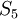 ?
?
פתרון. הומומורפיזם f כזה נקבע על-ידי תמונת האיבר 1, אבל התמונה מקיימת 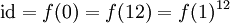 , ולכן היא מסדר המחלק את 12. בחבורה
, ולכן היא מסדר המחלק את 12. בחבורה 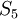 יש רק מחלקת צמידות אחת שהסדר של אברים בה אינו מחלק את 12, ובה 24 אברים; לכן מספר ההומומורפיזמים הוא 120-24=96.
יש רק מחלקת צמידות אחת שהסדר של אברים בה אינו מחלק את 12, ובה 24 אברים; לכן מספר ההומומורפיזמים הוא 120-24=96.