מכינה למחלקת מתמטיקה/מערכי שיעור/3: הבדלים בין גרסאות בדף
| (9 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 2: | שורה 2: | ||
==מוטיבציה לחקר הפונקציות הטריגונומטריות== | ==מוטיבציה לחקר הפונקציות הטריגונומטריות== | ||
כפי שנתאר למטה, הפונקציות הטריגונומטריות הן פונקציות מחזוריות שצורתן נובע מהיחס בין צלעות משולשים ישרי זוית. על כן, השימוש הראשון בפונקציות הטריגונומטריות יהיה בעת חישובים גיאומטריים כמו חישוב תאוצה על חפץ במדרון (פיסיקה), חישוב נקודות מפגש של קווים (ארכיטקטורה, אמנות, הנדסה), תדרי קול (מוזיקה), תדרי גלים | כפי שנתאר למטה, הפונקציות הטריגונומטריות הן פונקציות מחזוריות שצורתן נובע מהיחס בין צלעות משולשים ישרי זוית. על כן, השימוש הראשון בפונקציות הטריגונומטריות יהיה בעת חישובים גיאומטריים כמו חישוב תאוצה על חפץ במדרון (פיסיקה), חישוב נקודות מפגש של קווים (ארכיטקטורה, אמנות, הנדסה), תדרי קול (מוזיקה), תדרי גלים אלקטרומגנטיים (ראייה, צילום, תקשורת אלחוטית), ועוד. | ||
נוסף על כך, ישנם גם קשרים מיוחדים בין הפונקציות הטריגונומטריות לפונקציות שימושיות אחרות במתמטיקה. למשל, כפי שנראה בהמשך, השטח מתחת לפונקציה <math>\frac{1}{1+x^2}</math> הוא סוג של פונקציה טריגונומטרית. | נוסף על כך, ישנם גם קשרים מיוחדים בין הפונקציות הטריגונומטריות לפונקציות שימושיות אחרות במתמטיקה. למשל, כפי שנראה בהמשך, השטח מתחת לפונקציה <math>\frac{1}{1+x^2}</math> הוא סוג של פונקציה טריגונומטרית. | ||
| שורה 15: | שורה 15: | ||
*<math>sin(t)</math> מוגדר להיות ערך ציר ה-<math>y</math> של הנקודה על מעגל היחידה הממוקמת במרחק של <math>t</math> | *<math>sin(t)</math> מוגדר להיות ערך ציר ה-<math>y</math> של הנקודה על מעגל היחידה הממוקמת במרחק של <math>t</math> כנגד כיוון השעון (תחילת הסיבובים בנקודה <math>(1,0)</math>) | ||
*<math>cos(t)</math> מוגדר להיות ערך ציר ה-<math>x</math> של הנקודה על מעגל היחידה הממוקמת במרחק של <math>t</math> | *<math>cos(t)</math> מוגדר להיות ערך ציר ה-<math>x</math> של הנקודה על מעגל היחידה הממוקמת במרחק של <math>t</math> כנגד כיוון השעון (תחילת הסיבובים בנקודה <math>(1,0)</math>) | ||
| שורה 29: | שורה 29: | ||
*<math>cot(t):= \frac{cos(t)}{sin(t)}=\frac{1}{tan(t)}</math> | *<math>cot(t):= \frac{cos(t)}{sin(t)}=\frac{1}{tan(t)}</math> | ||
==דגשים חשובים על ערכי הפונקציות הטריגונומטריות== | |||
כפי שקל לראות מהתבננות במעגל היחידה מתקימות התכונות הבאות: | |||
*<math>-1\leq sin(x),cos(x)\leq 1</math> | |||
*<math>sin(0)=0, sin (\pi/2) = 1, sin(\pi)=0, sin(3\pi/2)=-1</math> | |||
*<math>cos(0)=1, cos (\pi/2) = 0, cos(\pi)=-1, cos(3\pi/2)=0</math> | |||
*מחזור <math>2\pi</math>: לכל מספר שלם k מתקיים <math>sin(x+2\pi k) = sin(x), cos(x+2\pi k) = cos(x)</math> | |||
'''תרגיל''': חשב את <math>sin(\pi/4)</math> | |||
| שורה 71: | שורה 87: | ||
*<math>cos(x+y)=cos(x)cos(y)-sin(x)sin(y)</math> | *<math>cos(x+y)=cos(x)cos(y)-sin(x)sin(y)</math> | ||
==תרגילים== | |||
'''תרגיל''': הוכח את הזהויות הטריגונומטריות של זוית כפולה לעיל. | |||
'''תרגיל''': הוכח את הזהות הטריגונומטרית <math>2sin(\alpha)sin(\beta)=cos(\alpha-\beta)-cos(\alpha+\beta)</math> | |||
'''תרגיל''': הוכח כי לכל מספר שלם n מתקיים <math>\Big|S_n\Big|=\Big|sin(1)+sin(2)+...+sin(n)\Big|\leq \frac{2}{sin(1)}</math> | |||
'''פתרון''': | |||
נכפול את בקבוע <math>2sin(1)</math> לקבל | |||
::<math>2sin(1)sin(1)+2sin(2)sin(1)+...+2sin(n)sin(1)</math> | |||
נפעיל את הזהות הטריגונומטרית <math>2sin(\alpha)sin(\beta)=cos(\alpha-\beta)-cos(\alpha+\beta)</math> | |||
::<math>cos(0)-cos(2)+cos(1)-cos(3)+cos(2)-cos(4)+...+cos(n-1)-cos(n+1)</math> | |||
נמחק את הביטויים שמצטמצמים ונקבל: | |||
::<math>cos(0)+cos(1)-cos(n)-cos(n+1)</math> | |||
ולכן <math>\Big|S_n\Big|=\Big|\frac{cos(0)+cos(1)-cos(n)-cos(n+1)}{2sin(1)}\Big|\leq \frac{4}{2sin(1)}= \frac{2}{sin(1)}</math> | |||
גרסה אחרונה מ־10:05, 11 באוגוסט 2022
מוטיבציה לחקר הפונקציות הטריגונומטריות
כפי שנתאר למטה, הפונקציות הטריגונומטריות הן פונקציות מחזוריות שצורתן נובע מהיחס בין צלעות משולשים ישרי זוית. על כן, השימוש הראשון בפונקציות הטריגונומטריות יהיה בעת חישובים גיאומטריים כמו חישוב תאוצה על חפץ במדרון (פיסיקה), חישוב נקודות מפגש של קווים (ארכיטקטורה, אמנות, הנדסה), תדרי קול (מוזיקה), תדרי גלים אלקטרומגנטיים (ראייה, צילום, תקשורת אלחוטית), ועוד.
נוסף על כך, ישנם גם קשרים מיוחדים בין הפונקציות הטריגונומטריות לפונקציות שימושיות אחרות במתמטיקה. למשל, כפי שנראה בהמשך, השטח מתחת לפונקציה [math]\displaystyle{ \frac{1}{1+x^2} }[/math] הוא סוג של פונקציה טריגונומטרית.
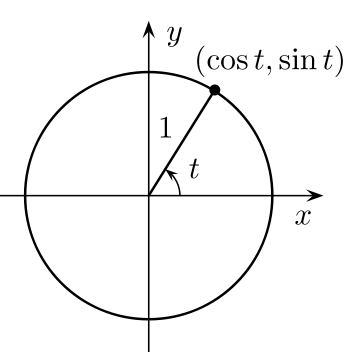
הגדרת הפונקציות הטריגונומטריות באמצעות מעגל היחידה
במעגל ישנן 360 מעלות השקולות ל[math]\displaystyle{ 2\pi }[/math] רדיאנים, וידוע כי היקף מעגל עם רדיוס r הינו [math]\displaystyle{ 2\pi r }[/math]. בלימודי המתמטיקה נשתמש בלבד בשיטת הרדיאנים לפיה הזוית בין שני ישרים היא אורך קטע הקשת שהם פורסים ממעגל היחידה (כלומר, מעגל עם רדיוס אחד שמרכזו בראשית הצירים).
נגדיר את הפונקציות הטריגונומטריות באמצעות מעגל היחידה.
- [math]\displaystyle{ sin(t) }[/math] מוגדר להיות ערך ציר ה-[math]\displaystyle{ y }[/math] של הנקודה על מעגל היחידה הממוקמת במרחק של [math]\displaystyle{ t }[/math] כנגד כיוון השעון (תחילת הסיבובים בנקודה [math]\displaystyle{ (1,0) }[/math])
- [math]\displaystyle{ cos(t) }[/math] מוגדר להיות ערך ציר ה-[math]\displaystyle{ x }[/math] של הנקודה על מעגל היחידה הממוקמת במרחק של [math]\displaystyle{ t }[/math] כנגד כיוון השעון (תחילת הסיבובים בנקודה [math]\displaystyle{ (1,0) }[/math])
- [math]\displaystyle{ tan(t):=\frac{sin(t)}{cos(t)} }[/math]
- [math]\displaystyle{ cot(t):= \frac{cos(t)}{sin(t)}=\frac{1}{tan(t)} }[/math]
דגשים חשובים על ערכי הפונקציות הטריגונומטריות
כפי שקל לראות מהתבננות במעגל היחידה מתקימות התכונות הבאות:
- [math]\displaystyle{ -1\leq sin(x),cos(x)\leq 1 }[/math]
- [math]\displaystyle{ sin(0)=0, sin (\pi/2) = 1, sin(\pi)=0, sin(3\pi/2)=-1 }[/math]
- [math]\displaystyle{ cos(0)=1, cos (\pi/2) = 0, cos(\pi)=-1, cos(3\pi/2)=0 }[/math]
- מחזור [math]\displaystyle{ 2\pi }[/math]: לכל מספר שלם k מתקיים [math]\displaystyle{ sin(x+2\pi k) = sin(x), cos(x+2\pi k) = cos(x) }[/math]
תרגיל: חשב את [math]\displaystyle{ sin(\pi/4) }[/math]
זהויות טריגונומטריות
ישנן זהויות טריגונומטריות רבות, ניתן לעיין ברשימה מלאה למדי בויקיפדיה. בשיעור זה נזכיר חלק מן הזהויות הבסיסיות.
ראשית נביט במשולש הנוצר בין הנקודות:
- [math]\displaystyle{ O=(0,0),B=(cos(t),sin(t)),C=(cos(t),0) }[/math]
זהו משולש ישר זוית עם יתר OB שהוא רדיוס המעגל ולכן באורך אחד, ושתי צלעות באורכי [math]\displaystyle{ |BC|=sin(t),|OC|=cos(t) }[/math]
לפי משפט פתגורס במשולש ישר זוית אנו מסיקים את הזהות הראשונה:
- [math]\displaystyle{ sin^2(t)+cos^2(t)=1 }[/math]
זהויות נוספות שחובה לדעת בעל פה, הן:
- [math]\displaystyle{ sin(-x)=-sin(x) }[/math]
- [math]\displaystyle{ cos(-x)=cos(x) }[/math]
- [math]\displaystyle{ sin(2x)=2sin(x)cos(x) }[/math]
- [math]\displaystyle{ cos(2x)=cos^2(x)-sin^2(x)=2cos^2(x)-1=1-2sin^2(x)=\frac{1-tan^2x}{1+tan^2x} }[/math]
- [math]\displaystyle{ sin(x+y)=sin(x)cos(y)+cos(x)sin(y) }[/math]
- [math]\displaystyle{ cos(x+y)=cos(x)cos(y)-sin(x)sin(y) }[/math]
תרגילים
תרגיל: הוכח את הזהויות הטריגונומטריות של זוית כפולה לעיל.
תרגיל: הוכח את הזהות הטריגונומטרית [math]\displaystyle{ 2sin(\alpha)sin(\beta)=cos(\alpha-\beta)-cos(\alpha+\beta) }[/math]
תרגיל: הוכח כי לכל מספר שלם n מתקיים [math]\displaystyle{ \Big|S_n\Big|=\Big|sin(1)+sin(2)+...+sin(n)\Big|\leq \frac{2}{sin(1)} }[/math]
פתרון:
נכפול את בקבוע [math]\displaystyle{ 2sin(1) }[/math] לקבל
- [math]\displaystyle{ 2sin(1)sin(1)+2sin(2)sin(1)+...+2sin(n)sin(1) }[/math]
נפעיל את הזהות הטריגונומטרית [math]\displaystyle{ 2sin(\alpha)sin(\beta)=cos(\alpha-\beta)-cos(\alpha+\beta) }[/math]
- [math]\displaystyle{ cos(0)-cos(2)+cos(1)-cos(3)+cos(2)-cos(4)+...+cos(n-1)-cos(n+1) }[/math]
נמחק את הביטויים שמצטמצמים ונקבל:
- [math]\displaystyle{ cos(0)+cos(1)-cos(n)-cos(n+1) }[/math]
ולכן [math]\displaystyle{ \Big|S_n\Big|=\Big|\frac{cos(0)+cos(1)-cos(n)-cos(n+1)}{2sin(1)}\Big|\leq \frac{4}{2sin(1)}= \frac{2}{sin(1)} }[/math]