משתמש:אור שחף/133 - הרצאה/20.2.11: הבדלים בין גרסאות בדף
(←הוכחה) |
מ (←הקדמה - הגדרות) |
||
| (12 גרסאות ביניים של 4 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
{{כותרת נושא|אינטגרציה|נושא ראשון}} | |||
''' | '''הערה:''' האינטגרל הוא '''לא''' שטח שמתחת לגרף. למעשה, השטח מתחת לגרף מוגדר לפי האינטגרל. | ||
===דוגמת חישוב (ידני) של שטח שמתחת לגרף=== | |||
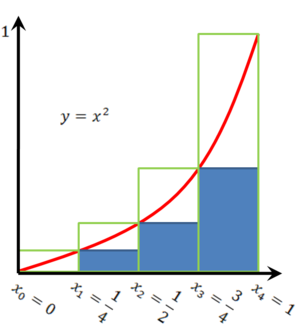
[[קובץ:השטח מתחת ל-x בריבוע לפי מלבנים.png|300px|ממוזער|ימין|הגרף של <math>y=x^2</math> והמלבנים החוסמים (עם גבול ירוק) והחסומים (בצבע כחול).]] | |||
נתון הגרף של <math>y=x^2</math> ונרצה לחשב את השטח שמתחת לו בקטע <math>[0,1]</math>. | |||
נחלק את הקטע: | |||
{{left|<math>0=x_0<x_1<x_2<\dots<x_n=1</math>}} | {{left|<math>0=x_0<x_1<x_2<\dots<x_n=1</math>}} | ||
כך שבאופן כללי <math>x_k=k/n</math> (בגרף מוצג המקרה הפרטי <math>n=4</math>). | |||
מעל כל תת קטע | מעל כל תת קטע <math>[x_{k-1},x_k]</math> נבנה "מלבן חוסם" שגובהו <math>\left({k\over n}\right)^2=x_k^2</math>. שטח כל המלבנים הללו הוא "שטח חוסם" {{left|<math>\overline S:=\sum_{k=1}^n\frac1n\left({k\over n}\right)^2=\frac1{n^3}\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6n^3}</math>}} | ||
כמו כן, מעל כל קטע | כמו כן, מעל כל תת קטע <math>[x_{k-1},x_k]</math> נבנה "מלבן חסום" שגובהו <math>\left({k-1\over n}\right)^2=x_{k-1}^2</math>. ביחד מלבנים אלה מהווים "שטח חסום" {{left|<math>\underline S:=\frac1n\sum_{k=1}^n\left({k-1\over n}\right)^2=\frac1{n^3}\sum_{k=1}^n(k-1)^2=\frac1{n^3}\sum_{k=1}^{n-1}k^2=\frac{(n-1)n(2n-1)}{6n^3}</math>}} | ||
כעת אם A מציין את השטח שמתחת לגרף בוודאי ש-<math>\underline S\le A\le\overline S</math>, ז"א <math>\frac{ | כעת, אם A מציין את השטח שמתחת לגרף, בוודאי ש-<math>\underline S\le A\le\overline S</math>, ז"א <math>\frac{(n-1)(2n-1)}{6n^2}\le A\le\frac{(n+1)(2n+1)}{6n^2}</math>. הדבר נכון לכל <math>n\in\mathbb N</math> ולכן נוכל להשאיף את <math>n\to\infty</math> ולקבל | ||
<math>\frac13\le A\le\frac13</math>, לכן <math>A=\frac13</math>. {{משל}} | <math>\frac13\le A\le\frac13</math>, לכן <math>A=\frac13</math>. {{משל}} | ||
---- | |||
'''הגדרה:''' תהי | '''הגדרה:''' תהי f מוגדרת בקטע I. נאמר שהפונקציה F קדומה ל-f ב-I אם <math>\forall x\in I:\ F'(x)=f(x)</math>. | ||
''דוגמה:'' אם <math>f(x)=x^2</math> אז <math>F(x)=\frac{x^3}3</math>. | ''דוגמה:'' אם <math>f(x)=x^2</math> אז <math>F(x)=\frac{x^3}3</math>. | ||
==משפט 0== | |||
אם | אם F ו-G קדומות ל-f בקטע I אז קיים קבוע c כך ש-<math>F(x)=G(x)+c</math> | ||
===הוכחה=== | |||
נגדיר <math>H(x)=F(x)-G(x)</math> ולכן <math>\forall x\in I:\ H'(x)=F'(x)-G'(x)=f(x)-f(x)=0</math>. | נגדיר <math>H(x)=F(x)-G(x)</math> ולכן <math>\forall x\in I:\ H'(x)=F'(x)-G'(x)=f(x)-f(x)=0</math>. מכאן ש-H היא פונקציה קבועה ולכן יש קבוע c כך ש-<math>F(x)-G(x)=H(x)=c\implies F(x)=G(x)+c</math>. {{משל}} | ||
---- | |||
'''הגדרה אינטואיטיבית:''' תהי <math>f(x)\ge0</math> רציפה בקטע <math>[a,b]</math>. נסמן ב-<math>\int\limits_a^b f</math> את השטח שמתחת לגרף. | |||
==המשפט היסודי של חשבון אינטגרלי {{הערה|(בצורה אינטואיטיבית)}}== | |||
תהי <math>f(x)\ge0</math> מוגדרת ורציפה ב-<math>[a,b]</math>. | תהי <math>f(x)\ge0</math> מוגדרת ורציפה ב-<math>[a,b]</math>. | ||
# לכל <math>x\in[a,b]</math> נגדיר <math>A(x)=\int\limits_a^x f | # לכל <math>x\in[a,b]</math> נגדיר <math>A(x)=\int\limits_a^x f</math> אזי <math>\forall x\in[a,b]:\ f(x)=A'(x)</math>. | ||
# אם | # אם F קדומה ל-f ב-<math>[a,b]</math> אז <math>\int\limits_a^b f=F(b)-F(a)</math>. | ||
== | ===הוכחה=== | ||
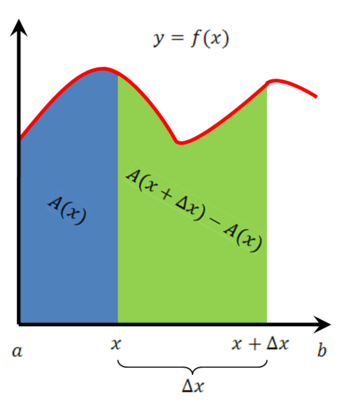
[[קובץ:הוכחה אינטואיטיבית למשפט היסודי של החשבון האינפיניטסימלי.png|ימין|ממוזער|350px]] | |||
# יהי x נתון. לפי ההגדרה <math>A'(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x}</math>. בגרף: <math>=A(x+\Delta x)-A(x)</math> השטח של החלק הירוק ו-<math>=\Delta x</math> בסיס החלק הירוק. לפיכך <math>=\frac{A(x+\Delta x)-A(x)}{\Delta x}</math> הגובה הממוצע של הפונקציה בחלק הירוק. לכן <math>=A'(x)</math> הגובה הממוצע של החלק הירוק (כאשר <math>\Delta x\to0</math>) <math>f(x)=</math>. {{משל}} | |||
# נתונה פונקציה קדומה F. מחלק 1 ידוע גם ש-A פונקציה קדומה (של f). לפי משפט 0 יש קבוע c כך ש-<math>F(x)=A(x)+c</math> ולכן <math>F(b)-F(a)=A(b)+c-(\underbrace{A(a)}_{=0}+c)=A(b)=\int\limits_a^b f</math>. {{משל}} | |||
=האינטגרל לפי דרבו= | |||
<math> | ==הקדמה - הגדרות== | ||
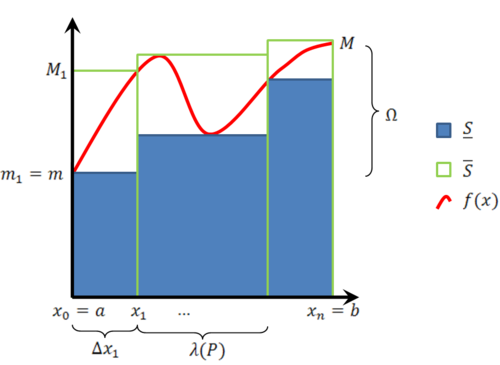
[[קובץ:הגדרת הערכים באינטגרל לפי דרבו.png|שמאל|500px|ממוזער]] | |||
תהי f מוגדרת וחסומה ע"י <math>m:=\inf f</math> ו- <math>M:=\sup f</math> בקטע <math>[a,b]</math>. נגדיר את התנודה של f ע"י <math>\Omega:=M-m</math>. כעת נגדיר חלוקה P של <math>[a,b]</math> כקבוצה <math>\{x_0,x_1,\dots,x_n\}</math> המקיימת: <math>a=x_0<x_1<\dots<x_n=b</math>. עוד נגדיר לכל k את אורך תת קטע מספר k להיות <math>\Delta x_k:=x_k-x_{k-1}</math> ואת הפרמטר של P להיות <math>\lambda(P):=\max_{k=1}^n\Delta x_k</math>. | |||
לכל k כך ש-<math>1\le k\le n</math> נגדיר גם <math>M_k:=\sup\{f(x):\ x_{k-1}\le x\le x_k\}</math> וכן <math>m_k:=\inf\{f(x):\ x_{k-1}\le x\le x_k\}</math>. בהתאם לכך נגדיר: | |||
* שטח חוסם - הסכום העליון: <math>\overline S(f,P):=\sum_{k=1}^n M_k\Delta x_k</math> | |||
* שטח חסום - הסכום התחתון: <math>\underline S(f,P):=\sum_{k=1}^n m_k\Delta x_k</math> | |||
==משפט 1== | |||
בסימונים הנ"ל, עבור כל חלוקה P מתקיים <math>m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)</math>. | בסימונים הנ"ל, עבור כל חלוקה P מתקיים <math>m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)</math>. | ||
===הוכחה=== | |||
{| | {| | ||
{{=|l=m(b-a) | {{=|l=m(b-a) | ||
|r=\sum_{k=1}^n m\Delta x_k | |r=\sum_{k=1}^n m\Delta x_k | ||
|c=<math>\sum_{k=1}^n\Delta x_k</math> | |c=<math>=\sum_{k=1}^n\Delta x_k</math> סכום כל הרווחים בין n נקודות החלוקה <math>b-a=</math>, לכן: | ||
}} | }} | ||
{{=|r=\sum_{k=1}^n m_k\Delta x_k=\underline S(f,P) | {{=|r=\sum_{k=1}^n m_k\Delta x_k=\underline S(f,P) | ||
| שורה 93: | שורה 78: | ||
נשים לב כי לפי משפט 1 המספרים <math>\overline S(f,P),\underline S(f,P)</math> חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f). | נשים לב כי לפי משפט 1 המספרים <math>\overline S(f,P),\underline S(f,P)</math> חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f). | ||
לכן מוגדרים היטב ה"אינטגרל העליון" <math>\overline{\int}_a^b f | לכן מוגדרים היטב ה"אינטגרל העליון" <math>\overline{\int}_a^b f:=\inf_P \overline S(f,P)</math> ו"האינטגרל התחתון" <math>\underline\int_a^b f:=\sup_P \underline S(f,P)</math>. | ||
==הגדרת האינטגרל לפי דרבו== | |||
תהי | תהי f מוגדרת וחסומה ב-<math>[a,b]</math>. נאמר ש-f אינטגרבילית לפי דרבו ב-<math>[a,b]</math> אם <math>\underline\int_a^b f=\overline{\int}_a^b f</math> ואם הם שווים אז נגדיר <math>\int\limits_a^b f</math> להיות הערך המשותף של <math>\underline\int f</math> ו-<math>\overline{\int} f</math>. | ||
===דוגמה=== | |||
בקטע <math>[a,b]</math> כלשהו נגדיר את פונקצית דיריכלה <math>D(x)=\begin{cases} | בקטע <math>[a,b]</math> כלשהו נגדיר את פונקצית דיריכלה <math>D(x)=\begin{cases}1&x\in\mathbb Q\\0&x\not\in\mathbb Q\end{cases}</math>. | ||
נקח חלוקה כלשהי ל-<math>[a,b]</math>: <math>a=x_0<x_1<\dots<x_n=b</math>. | נקח חלוקה כלשהי ל-<math>[a,b]</math>: <math>a=x_0<x_1<\dots<x_n=b</math>. | ||
לכל k מתקיים <math>M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}=1</math> וכן <math>m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}=0</math>. לכן <math>\overline S(f,P)=\sum_{k=1}^n M_k\Delta x_k=\sum_{k=1}^n 1\Delta x_k=b-a</math> ואילו <math>\underline S(f,P)=\sum_{k=1}^n m_k\Delta x_k=\sum_{k=1}^n 0\Delta x_k=0</math>. | לכל k מתקיים <math>M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}=1</math> וכן <math>m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}=0</math>. לכן <math>\overline S(f,P)=\sum_{k=1}^n M_k\Delta x_k=\sum_{k=1}^n 1\Delta x_k=b-a</math> ואילו <math>\underline S(f,P)=\sum_{k=1}^n m_k\Delta x_k=\sum_{k=1}^n 0\Delta x_k=0</math>. מכאן <math>\underline\int_a^b f=\sup_P \underline S(f,P)=0</math> ו-<math>\overline{\int}_a^b f=\inf_P \overline S(f,P)=b-a</math>, וכייוון שאינם שווים f אינה אינטגרבילית. {{משל}} | ||
מכאן <math>\underline\int_a^b f | |||
---- | |||
'''הגדרה:''' תהי P חלוקה של קטע <math>[a,b]</math>. חלוקה Q של <math>[a,b]</math> נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות. | '''הגדרה:''' תהי P חלוקה של קטע <math>[a,b]</math>. חלוקה Q של <math>[a,b]</math> נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות. | ||
==משפט 2== | |||
תהי | תהי f מוגדרת וחסומה ב-<math>[a,b]</math>, תהי P חלוקה של <math>[a,b]</math> ו-Q עידון של P ע"י הוספת r נקודות. אזי | ||
{{left| | {{left| | ||
<math>0\le\overline S(f,P)-\overline S(f,Q)\le r\lambda(P)\Omega</math> | <math>0\le\overline S(f,P)-\overline S(f,Q)\le r\lambda(P)\Omega</math> | ||
| שורה 122: | שורה 106: | ||
כלומר, הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-<math>r\lambda(P)\Omega</math>. | כלומר, הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-<math>r\lambda(P)\Omega</math>. | ||
===הוכחה=== | |||
מקרה ראשון: <math>r=1</math>. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת <math>x_i'</math> כך ש-<math>x_{i-1}<x_i'<x_i</math> עבור i כלשהו. בהתאם לכך נגדיר <math>M_i^-:=\sup\{f(x):\ x_{i-1}\le x\le x_i'\}</math> ו-<math>M_i^+:=\sup\{f(x):\ x_i'\le x\le x_i\}</math>. | מקרה ראשון: <math>r=1</math>. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת <math>x_i'</math> כך ש-<math>x_{i-1}<x_i'<x_i</math> עבור i כלשהו. בהתאם לכך נגדיר <math>M_i^-:=\sup\{f(x):\ x_{i-1}\le x\le x_i'\}</math> ו-<math>M_i^+:=\sup\{f(x):\ x_i'\le x\le x_i\}</math>. | ||
כמו כן, לא שינינו כל תת קטע <math>[x_{k-1},x_k]</math> עבור <math>k\not=i</math> כלשהו. לכן <math>\overline S(f,P)-\overline S(f,Q)=M_i\Delta x_i-\Big(M_i^-(x_i'-x_{i-1})+M_i^+(x_i-x_i')\Big)</math> | כמו כן, לא שינינו כל תת קטע <math>[x_{k-1},x_k]</math> עבור <math>k\not=i</math> כלשהו. לכן <math>\overline S(f,P)-\overline S(f,Q)=M_i\Delta x_i-\Big(M_i^-(x_i'-x_{i-1})+M_i^+(x_i-x_i')\Big)</math> | ||
| שורה 128: | שורה 112: | ||
לפי ההגדרות <math>M_i\ge M_i^+,M_i^-</math> ולפיכך {{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\ge M_i\Delta x_i-\Big(M_i(x_i'-x_{i-1})+M_i(x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i'-x_{i-1}+x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i-x_{i-1})\Big)\\&=0\end{align}</math>}} | לפי ההגדרות <math>M_i\ge M_i^+,M_i^-</math> ולפיכך {{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\ge M_i\Delta x_i-\Big(M_i(x_i'-x_{i-1})+M_i(x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i'-x_{i-1}+x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i-x_{i-1})\Big)\\&=0\end{align}</math>}} | ||
{{ | {{המשך סיכום|תאריך=22.2.11}} | ||
כמו כן, <math>\overline S(f,P)-\overline S(f,Q)\le | כמו כן, | ||
{{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\le M_i(x_i-x_{i-1})-m_i(x_i-x_{i-1})\\&=(M_i-m_i)(x_i-x_{i-1})\\&\le\Omega(x_i-x_{i-1})\\&\le\underbrace{r}_{=1}\lambda(P)\Omega\end{align}</math>}} | |||
מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר <math>\Omega\lambda(P)</math>. לכן מיד נסיק <math>0\le\overline S(f,P)-\overline S(f,Q)\le r\Omega\lambda(P)</math>. | מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר <math>\Omega\lambda(P)</math> בכל אחת מ-r המפעמים. לכן מיד נסיק <math>0\le\overline S(f,P)-\overline S(f,Q)\le r\Omega\lambda(P)</math>. | ||
ההוכחה לסכום תחתון דומה. {{משל}} | ההוכחה לסכום תחתון דומה. {{משל}} | ||
===מסקנה 1=== | |||
נקח f כנ"ל ונניח ש-P ו-Q הן שתי חלוקות כלשהן של <math>[a,b]</math>. אזי <math>\underline S(f,P)\le\overline S(f,Q)</math>. | |||
====הוכחה==== | |||
נבנה עידון משותף, ז"א <math>R=P\cup Q</math>. לפי משפט 2 מתקיים <math>\underline S(f,P)\le\underline S(f,R)\le \overline S(f,R)\le\overline S(f,Q)</math>. {{משל}} | |||
===מסקנה 2=== | |||
עבור f כנ"ל מתקיים <math>\underline\int_a^b f\le\overline{\int}_a^b f</math>. | |||
====הוכחה==== | |||
מסקנה 1 אומרת שלכל שתי חלוקות P,Q של <math>[a,b]</math> מתקיים <math>\underline S(f,P)\le\overline S(f,Q)</math> ולכן <math>\sup_P\underline S(f,P)\le\inf_Q\overline S(f,Q)</math>. כמו כן, לפי ההגדרה <math>\underline\int_a^b f=\sup_Q\underline S(f,Q)</math> ו-<math>\inf_P\overline S(f,P)=\overline{\int}_a^b f</math>. {{משל}} | |||
גרסה אחרונה מ־14:17, 12 באוגוסט 2013
נושא ראשון:
אינטגרציה
הערה: האינטגרל הוא לא שטח שמתחת לגרף. למעשה, השטח מתחת לגרף מוגדר לפי האינטגרל.
דוגמת חישוב (ידני) של שטח שמתחת לגרף
נתון הגרף של [math]\displaystyle{ y=x^2 }[/math] ונרצה לחשב את השטח שמתחת לו בקטע [math]\displaystyle{ [0,1] }[/math]. נחלק את הקטע:
כך שבאופן כללי [math]\displaystyle{ x_k=k/n }[/math] (בגרף מוצג המקרה הפרטי [math]\displaystyle{ n=4 }[/math]).
מעל כל תת קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] נבנה "מלבן חוסם" שגובהו [math]\displaystyle{ \left({k\over n}\right)^2=x_k^2 }[/math]. שטח כל המלבנים הללו הוא "שטח חוסם"
כמו כן, מעל כל תת קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] נבנה "מלבן חסום" שגובהו [math]\displaystyle{ \left({k-1\over n}\right)^2=x_{k-1}^2 }[/math]. ביחד מלבנים אלה מהווים "שטח חסום"
כעת, אם A מציין את השטח שמתחת לגרף, בוודאי ש-[math]\displaystyle{ \underline S\le A\le\overline S }[/math], ז"א [math]\displaystyle{ \frac{(n-1)(2n-1)}{6n^2}\le A\le\frac{(n+1)(2n+1)}{6n^2} }[/math]. הדבר נכון לכל [math]\displaystyle{ n\in\mathbb N }[/math] ולכן נוכל להשאיף את [math]\displaystyle{ n\to\infty }[/math] ולקבל [math]\displaystyle{ \frac13\le A\le\frac13 }[/math], לכן [math]\displaystyle{ A=\frac13 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
הגדרה: תהי f מוגדרת בקטע I. נאמר שהפונקציה F קדומה ל-f ב-I אם [math]\displaystyle{ \forall x\in I:\ F'(x)=f(x) }[/math].
דוגמה: אם [math]\displaystyle{ f(x)=x^2 }[/math] אז [math]\displaystyle{ F(x)=\frac{x^3}3 }[/math].
משפט 0
אם F ו-G קדומות ל-f בקטע I אז קיים קבוע c כך ש-[math]\displaystyle{ F(x)=G(x)+c }[/math]
הוכחה
נגדיר [math]\displaystyle{ H(x)=F(x)-G(x) }[/math] ולכן [math]\displaystyle{ \forall x\in I:\ H'(x)=F'(x)-G'(x)=f(x)-f(x)=0 }[/math]. מכאן ש-H היא פונקציה קבועה ולכן יש קבוע c כך ש-[math]\displaystyle{ F(x)-G(x)=H(x)=c\implies F(x)=G(x)+c }[/math]. [math]\displaystyle{ \blacksquare }[/math]
הגדרה אינטואיטיבית: תהי [math]\displaystyle{ f(x)\ge0 }[/math] רציפה בקטע [math]\displaystyle{ [a,b] }[/math]. נסמן ב-[math]\displaystyle{ \int\limits_a^b f }[/math] את השטח שמתחת לגרף.
המשפט היסודי של חשבון אינטגרלי (בצורה אינטואיטיבית)
תהי [math]\displaystyle{ f(x)\ge0 }[/math] מוגדרת ורציפה ב-[math]\displaystyle{ [a,b] }[/math].
- לכל [math]\displaystyle{ x\in[a,b] }[/math] נגדיר [math]\displaystyle{ A(x)=\int\limits_a^x f }[/math] אזי [math]\displaystyle{ \forall x\in[a,b]:\ f(x)=A'(x) }[/math].
- אם F קדומה ל-f ב-[math]\displaystyle{ [a,b] }[/math] אז [math]\displaystyle{ \int\limits_a^b f=F(b)-F(a) }[/math].
הוכחה
- יהי x נתון. לפי ההגדרה [math]\displaystyle{ A'(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x} }[/math]. בגרף: [math]\displaystyle{ =A(x+\Delta x)-A(x) }[/math] השטח של החלק הירוק ו-[math]\displaystyle{ =\Delta x }[/math] בסיס החלק הירוק. לפיכך [math]\displaystyle{ =\frac{A(x+\Delta x)-A(x)}{\Delta x} }[/math] הגובה הממוצע של הפונקציה בחלק הירוק. לכן [math]\displaystyle{ =A'(x) }[/math] הגובה הממוצע של החלק הירוק (כאשר [math]\displaystyle{ \Delta x\to0 }[/math]) [math]\displaystyle{ f(x)= }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- נתונה פונקציה קדומה F. מחלק 1 ידוע גם ש-A פונקציה קדומה (של f). לפי משפט 0 יש קבוע c כך ש-[math]\displaystyle{ F(x)=A(x)+c }[/math] ולכן [math]\displaystyle{ F(b)-F(a)=A(b)+c-(\underbrace{A(a)}_{=0}+c)=A(b)=\int\limits_a^b f }[/math]. [math]\displaystyle{ \blacksquare }[/math]
האינטגרל לפי דרבו
הקדמה - הגדרות
תהי f מוגדרת וחסומה ע"י [math]\displaystyle{ m:=\inf f }[/math] ו- [math]\displaystyle{ M:=\sup f }[/math] בקטע [math]\displaystyle{ [a,b] }[/math]. נגדיר את התנודה של f ע"י [math]\displaystyle{ \Omega:=M-m }[/math]. כעת נגדיר חלוקה P של [math]\displaystyle{ [a,b] }[/math] כקבוצה [math]\displaystyle{ \{x_0,x_1,\dots,x_n\} }[/math] המקיימת: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math]. עוד נגדיר לכל k את אורך תת קטע מספר k להיות [math]\displaystyle{ \Delta x_k:=x_k-x_{k-1} }[/math] ואת הפרמטר של P להיות [math]\displaystyle{ \lambda(P):=\max_{k=1}^n\Delta x_k }[/math].
לכל k כך ש-[math]\displaystyle{ 1\le k\le n }[/math] נגדיר גם [math]\displaystyle{ M_k:=\sup\{f(x):\ x_{k-1}\le x\le x_k\} }[/math] וכן [math]\displaystyle{ m_k:=\inf\{f(x):\ x_{k-1}\le x\le x_k\} }[/math]. בהתאם לכך נגדיר:
- שטח חוסם - הסכום העליון: [math]\displaystyle{ \overline S(f,P):=\sum_{k=1}^n M_k\Delta x_k }[/math]
- שטח חסום - הסכום התחתון: [math]\displaystyle{ \underline S(f,P):=\sum_{k=1}^n m_k\Delta x_k }[/math]
משפט 1
בסימונים הנ"ל, עבור כל חלוקה P מתקיים [math]\displaystyle{ m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a) }[/math].
הוכחה
| [math]\displaystyle{ =\sum_{k=1}^n\Delta x_k }[/math] סכום כל הרווחים בין n נקודות החלוקה [math]\displaystyle{ b-a= }[/math], לכן: | [math]\displaystyle{ }[/math] | [math]\displaystyle{ \sum_{k=1}^n m\Delta x_k }[/math] | [math]\displaystyle{ = }[/math] | [math]\displaystyle{ m(b-a) }[/math] | [math]\displaystyle{ }[/math] | |
| לכל k מתקיים [math]\displaystyle{ m\le m_k }[/math]. | [math]\displaystyle{ }[/math] | [math]\displaystyle{ \sum_{k=1}^n m_k\Delta x_k=\underline S(f,P) }[/math] | [math]\displaystyle{ \le }[/math] | [math]\displaystyle{ }[/math] | [math]\displaystyle{ }[/math] | |
| [math]\displaystyle{ }[/math] | [math]\displaystyle{ \sum_{k=1}^n M_k \Delta x_k=\overline S(f,P) }[/math] | [math]\displaystyle{ \le }[/math] | [math]\displaystyle{ }[/math] | [math]\displaystyle{ }[/math] | ||
| [math]\displaystyle{ }[/math] | [math]\displaystyle{ \sum_{k=1}^n M\Delta x_k }[/math] | [math]\displaystyle{ \le }[/math] | [math]\displaystyle{ }[/math] | [math]\displaystyle{ }[/math] | ||
| [math]\displaystyle{ }[/math] | [math]\displaystyle{ M(b-a) }[/math] | [math]\displaystyle{ = }[/math] | [math]\displaystyle{ }[/math] | [math]\displaystyle{ }[/math] |
[math]\displaystyle{ \blacksquare }[/math]
נשים לב כי לפי משפט 1 המספרים [math]\displaystyle{ \overline S(f,P),\underline S(f,P) }[/math] חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).
לכן מוגדרים היטב ה"אינטגרל העליון" [math]\displaystyle{ \overline{\int}_a^b f:=\inf_P \overline S(f,P) }[/math] ו"האינטגרל התחתון" [math]\displaystyle{ \underline\int_a^b f:=\sup_P \underline S(f,P) }[/math].
הגדרת האינטגרל לפי דרבו
תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. נאמר ש-f אינטגרבילית לפי דרבו ב-[math]\displaystyle{ [a,b] }[/math] אם [math]\displaystyle{ \underline\int_a^b f=\overline{\int}_a^b f }[/math] ואם הם שווים אז נגדיר [math]\displaystyle{ \int\limits_a^b f }[/math] להיות הערך המשותף של [math]\displaystyle{ \underline\int f }[/math] ו-[math]\displaystyle{ \overline{\int} f }[/math].
דוגמה
בקטע [math]\displaystyle{ [a,b] }[/math] כלשהו נגדיר את פונקצית דיריכלה [math]\displaystyle{ D(x)=\begin{cases}1&x\in\mathbb Q\\0&x\not\in\mathbb Q\end{cases} }[/math]. נקח חלוקה כלשהי ל-[math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math].
לכל k מתקיים [math]\displaystyle{ M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}=1 }[/math] וכן [math]\displaystyle{ m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}=0 }[/math]. לכן [math]\displaystyle{ \overline S(f,P)=\sum_{k=1}^n M_k\Delta x_k=\sum_{k=1}^n 1\Delta x_k=b-a }[/math] ואילו [math]\displaystyle{ \underline S(f,P)=\sum_{k=1}^n m_k\Delta x_k=\sum_{k=1}^n 0\Delta x_k=0 }[/math]. מכאן [math]\displaystyle{ \underline\int_a^b f=\sup_P \underline S(f,P)=0 }[/math] ו-[math]\displaystyle{ \overline{\int}_a^b f=\inf_P \overline S(f,P)=b-a }[/math], וכייוון שאינם שווים f אינה אינטגרבילית. [math]\displaystyle{ \blacksquare }[/math]
הגדרה: תהי P חלוקה של קטע [math]\displaystyle{ [a,b] }[/math]. חלוקה Q של [math]\displaystyle{ [a,b] }[/math] נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.
משפט 2
תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math], תהי P חלוקה של [math]\displaystyle{ [a,b] }[/math] ו-Q עידון של P ע"י הוספת r נקודות. אזי
[math]\displaystyle{ 0\le\overline S(f,P)-\overline S(f,Q)\le r\lambda(P)\Omega }[/math]
[math]\displaystyle{ 0\le\underline S(f,Q)-\underline S(f,P)\le r\lambda(P)\Omega }[/math]
(נזכיר ש-[math]\displaystyle{ \lambda(P)=\max_{1\le k\le n}\Delta x_k }[/math] ו-[math]\displaystyle{ \Omega=\sup_{x\in[a,b]} f(x)-\inf_{x\in[a,b]} f(x) }[/math])
כלומר, הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-[math]\displaystyle{ r\lambda(P)\Omega }[/math].
הוכחה
מקרה ראשון: [math]\displaystyle{ r=1 }[/math]. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת [math]\displaystyle{ x_i' }[/math] כך ש-[math]\displaystyle{ x_{i-1}\lt x_i'\lt x_i }[/math] עבור i כלשהו. בהתאם לכך נגדיר [math]\displaystyle{ M_i^-:=\sup\{f(x):\ x_{i-1}\le x\le x_i'\} }[/math] ו-[math]\displaystyle{ M_i^+:=\sup\{f(x):\ x_i'\le x\le x_i\} }[/math]. כמו כן, לא שינינו כל תת קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] עבור [math]\displaystyle{ k\not=i }[/math] כלשהו. לכן [math]\displaystyle{ \overline S(f,P)-\overline S(f,Q)=M_i\Delta x_i-\Big(M_i^-(x_i'-x_{i-1})+M_i^+(x_i-x_i')\Big) }[/math]
לפי ההגדרות [math]\displaystyle{ M_i\ge M_i^+,M_i^- }[/math] ולפיכך
את ההמשך עשינו בשיעור שאחריו:
כמו כן,
מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר [math]\displaystyle{ \Omega\lambda(P) }[/math] בכל אחת מ-r המפעמים. לכן מיד נסיק [math]\displaystyle{ 0\le\overline S(f,P)-\overline S(f,Q)\le r\Omega\lambda(P) }[/math].
ההוכחה לסכום תחתון דומה. [math]\displaystyle{ \blacksquare }[/math]
מסקנה 1
נקח f כנ"ל ונניח ש-P ו-Q הן שתי חלוקות כלשהן של [math]\displaystyle{ [a,b] }[/math]. אזי [math]\displaystyle{ \underline S(f,P)\le\overline S(f,Q) }[/math].
הוכחה
נבנה עידון משותף, ז"א [math]\displaystyle{ R=P\cup Q }[/math]. לפי משפט 2 מתקיים [math]\displaystyle{ \underline S(f,P)\le\underline S(f,R)\le \overline S(f,R)\le\overline S(f,Q) }[/math]. [math]\displaystyle{ \blacksquare }[/math]
מסקנה 2
עבור f כנ"ל מתקיים [math]\displaystyle{ \underline\int_a^b f\le\overline{\int}_a^b f }[/math].
הוכחה
מסקנה 1 אומרת שלכל שתי חלוקות P,Q של [math]\displaystyle{ [a,b] }[/math] מתקיים [math]\displaystyle{ \underline S(f,P)\le\overline S(f,Q) }[/math] ולכן [math]\displaystyle{ \sup_P\underline S(f,P)\le\inf_Q\overline S(f,Q) }[/math]. כמו כן, לפי ההגדרה [math]\displaystyle{ \underline\int_a^b f=\sup_Q\underline S(f,Q) }[/math] ו-[math]\displaystyle{ \inf_P\overline S(f,P)=\overline{\int}_a^b f }[/math]. [math]\displaystyle{ \blacksquare }[/math]