הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/22.2.11"
מ (בדיקה) |
|||
| (3 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | {{ | + | {{המשך הגיע|תיאור=משפט 2|תאריך=20.2.11}} |
=האינטגרל לפי דרבו {{הערה|(המשך)}}= | =האינטגרל לפי דרבו {{הערה|(המשך)}}= | ||
==משפט 3== | ==משפט 3== | ||
| − | תהי f | + | תהי f מוגדרת וחסומה ב-<math>[a,b]</math>. אזי <math>\underline\int_a^b f(x)\mathrm dx=\lim_{\lambda(P)\to0}\underline S(f,P)</math> וכן <math>\overline{\int}_a^b f(x)\mathrm dx=\lim_{\lambda(P)\to0}\overline S(f,P)</math>. |
===הוכחה=== | ===הוכחה=== | ||
| − | הטענה הראשונה אומרת שלכל <math>\varepsilon>0</math> קיים <math>\delta>0</math> כך שאם <math>\lambda(P)<\delta</math> | + | הטענה הראשונה אומרת שלכל <math>\varepsilon>0</math> קיים <math>\delta>0</math> כך שאם <math>|\lambda(P)|=\lambda(P)<\delta</math> אזי <math>\left|\overline S(f,P)-\overline{\int}_a^b f(x)\mathrm dx\right|<\varepsilon</math>. ברור מהגדרת האינטגרל העליון כי <math>0\le\overline S(f,P)-\overline{\int}_a^b f(x)\mathrm dx</math>. כעת יהי <math>\varepsilon>0</math> נתון. לפי הגדרת האינפימום קיימת חלוקה מסויימת Q של <math>[a,b]</math> כך ש-<math>0\le\overline S(f,Q)-\overline{\int}_a^b f(x)\mathrm dx<\frac\varepsilon2</math> ונניח של-Q יש r נקודות חלוקה. כעת נניח ש-P חלוקה כלשהי של <math>[a,b]</math> כך ש-<math>\lambda(P)<\frac\varepsilon{2r\Omega}</math>, ונגדיר <math>R=P\cup Q</math>. כיוון ש-R עידון של Q, <math>\overline{\int}_a^b f(x)\mathrm dx\le\overline S(f,R)\le\overline S(f,Q)</math> ונובע ש-<math>0\le\overline S(f,R)-\overline{\int}_a^b f(x)\mathrm dx\le\overline S(f,Q)-\overline{\int}_a^b f(x)\mathrm dx<\frac\varepsilon2</math>. אבל R התקבלה מ-P ע"י הוספה של לכל היותר r נקודות, לכן ע"פ משפט 2 ידוע ש-<math>\overline S(f,P)-\overline S(f,R)\le r\lambda(P)\Omega<r\Omega\frac\varepsilon{2r\Omega}=\frac\varepsilon2</math>. לכן נוכל להסיק |
| − | <math>0\le\overline S(f,P)-\overline{\int}_a^b f(x)dx=\overline S(f,P)-\overline S(f,R)+\overline S(f,R)-\overline{\int}_a^b f(x)dx<\frac\varepsilon2+\frac\varepsilon2=\varepsilon</math>. | + | <math>0\le\overline S(f,P)-\overline{\int}_a^b f(x)\mathrm dx=\overline S(f,P)-\overline S(f,R)+\overline S(f,R)-\overline{\int}_a^b f(x)\mathrm dx<\frac\varepsilon2+\frac\varepsilon2=\varepsilon</math>. |
ההוכחה לאינטגרל התחתון דומה. {{משל}} | ההוכחה לאינטגרל התחתון דומה. {{משל}} | ||
==משפט 4== | ==משפט 4== | ||
| − | תהי f כנ"ל. אזי f אינטגרבילית ב-<math>[a,b]</math> אם"ם <math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math> ואם כן <math>\int\limits_a^b f(x)dx=\lim_{\lambda(P)\to0}\overline S(f,P)=\lim_{\lambda(P)\to0}\underline S(f,P)</math>. | + | תהי f כנ"ל. אזי f אינטגרבילית ב-<math>[a,b]</math> אם"ם <math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math> ואם כן <math>\int\limits_a^b f(x)\mathrm dx=\lim_{\lambda(P)\to0}\overline S(f,P)=\lim_{\lambda(P)\to0}\underline S(f,P)</math>. |
===הוכחה=== | ===הוכחה=== | ||
| − | תחילה נניח ש-f אינטגרבילית, ז"א <math>\overline{\int}_a^b f(x)dx=\underline\int_a^b f(x)dx</math>. לכן, ממשפט 3, <math>\lim_{\lambda(P)\to0}\overline S(f,P)=\overline{\int}_a^b f(x)dx=\underline\int_a^b f(x)dx=\lim_{\lambda(P)\to0}\underline S(f,P)</math>. ע"פ אריתמטיקה של גבולות <math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math> וכן <math>\lim_{\lambda(P)\to0}\overline S(f,P)=\int_a^b f(x)dx=\lim_{\lambda(P)\to0}\underline S(f,P)</math>. | + | תחילה נניח ש-f אינטגרבילית, ז"א <math>\overline{\int}_a^b f(x)\mathrm dx=\underline\int_a^b f(x)\mathrm dx</math>. לכן, ממשפט 3, <math>\lim_{\lambda(P)\to0}\overline S(f,P)=\overline{\int}_a^b f(x)\mathrm dx=\underline\int_a^b f(x)\mathrm dx=\lim_{\lambda(P)\to0}\underline S(f,P)</math>. ע"פ אריתמטיקה של גבולות <math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math> וכן <math>\lim_{\lambda(P)\to0}\overline S(f,P)=\int_a^b f(x)\mathrm dx=\lim_{\lambda(P)\to0}\underline S(f,P)</math>. |
| − | עכשיו נניח ש-<math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math>. | + | עכשיו נניח ש-<math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math> ונוכיח את ההיפך. ממשפט 3 <math>0=\lim_{\lambda(P)\to0}\overline S(f,P)-\lim_{\lambda(P)\to0}\underline S(f,P)=\overline{\int}_a^b f(x)\mathrm dx-\underline\int_a^b f(x)\mathrm dx</math> ולכן f אינטגרבילית. {{משל}} |
==משפט 5== | ==משפט 5== | ||
| שורה 24: | שורה 24: | ||
אם נתון ש-f אינטגרבילית אז ממשפט 4 <math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math>. לכן עבור <math>\varepsilon>0</math> קיים <math>\delta>0</math> כך שלכל P המקיימת <math>\lambda(P)<\delta</math> מתקיים <math>\overline S(f,P)-\underline S(f,P)<\varepsilon</math>. | אם נתון ש-f אינטגרבילית אז ממשפט 4 <math>\lim_{\lambda(P)\to0}\overline S(f,P)-\underline S(f,P)=0</math>. לכן עבור <math>\varepsilon>0</math> קיים <math>\delta>0</math> כך שלכל P המקיימת <math>\lambda(P)<\delta</math> מתקיים <math>\overline S(f,P)-\underline S(f,P)<\varepsilon</math>. | ||
| − | לצד השני, נניח שלכל <math>\varepsilon>0</math> קיימת חלוקה P כך | + | לצד השני, נניח שלכל <math>\varepsilon>0</math> קיימת חלוקה P כך שמתקיים <math>\overline S(f,P)-\underline S(f,P)<\varepsilon</math>. כידוע, לכל חלוקה P מתקיים <math>\underline S(f,P)\le\underline\int_a^b f\le\overline{\int}_a^b f\le\overline S(f,P)</math>. לפי הנתון נקבל <math>0\le\overline{\int}_a^b f-\underline\int_a^b f<\varepsilon</math>. זה נכון לכל <math>\varepsilon>0</math> ולכן <math>\overline{\int}_a^b f-\underline\int_a^b f=0</math>, כלומר f אינטגרבילית ב-<math>[a,b]</math>. {{משל}} |
==משפט 6== | ==משפט 6== | ||
| − | תהי | + | תהי f רציפה ב-<math>[a,b]</math>. אזי f אינטגרבילית ב-<math>[a,b]</math>. |
===הוכחה=== | ===הוכחה=== | ||
| − | + | יהי <math>\varepsilon>0</math>. כיוון ש-f רציפה בקטע סגור <math>[a,b]</math> היא רציפה במ"ש, לכן קיים <math>\delta>0</math> כך שאם <math>x_1,x_2\in[a,b]</math> ו-<math>|x_1-x_2|<\delta</math> אז <math>|f(x_1)-f(x_2)|<\frac\varepsilon{b-a}</math>. כעת תהי P חלוקה כלשהי של <math>[a,b]</math> כך ש-<math>\lambda(P)<\delta</math>. לפיכך <math>\overline S(f,P)-\underline S(f,P)=\sum_{k=1}^n(M_k-m_k)\Delta x_k</math> כאשר <math>M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}</math> ו-<math>m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}</math>. כיוון ש-f רציפה ושעפ"י המשפט השני של ויירשראס לכל f רציפה ב-<math>[a,b]</math> יש שם נקודות מינימום ומקסימום, לכל k קיימים <math>y_k,z_k\in[x_{k-1},x_k]</math> כך ש-<math>f(y_k)=M_k</math> ו-<math>f(z_k)=m_k</math>. כעת <math>|y_k-z_k|\le x_k-x_{k-1}=\Delta x_k\le\lambda(P)<\delta</math>, לכן <math>M_k-m_k=|f(y_k)-f(z_k)|<\frac\varepsilon{b-a}</math> ולבסוף | |
| − | {{left|<math>\begin{align}\overline S(f,P)-\underline S(f,P)&=\sum_{k=1}^n(M_k-m_k)\Delta x_k\\&<\sum_{k=1}^n\frac\varepsilon{ | + | {{left|<math>\begin{align}\overline S(f,P)-\underline S(f,P)&=\sum_{k=1}^n(M_k-m_k)\Delta x_k\\&<\sum_{k=1}^n\frac\varepsilon{b-a}\Delta x_k\\&=\frac\varepsilon{b-a}(x_1-\underbrace{x_0}_{=a}+x_2-x_1+\dots+\underbrace{x_n}_{=b}-x_{n-1})\\&=\frac\varepsilon{b-a}(b-a)\\&=\varepsilon\end{align}</math>}} |
ונובע ממשפט 5 (או 4) ש-f אינטגרבילית ב-<math>[a,b]</math>. {{משל}} | ונובע ממשפט 5 (או 4) ש-f אינטגרבילית ב-<math>[a,b]</math>. {{משל}} | ||
| שורה 38: | שורה 38: | ||
תהי f מוגדרת ומונוטונית בקטע <math>[a,b]</math>. אזי f אינטגרבילית ב-<math>[a,b]</math>. | תהי f מוגדרת ומונוטונית בקטע <math>[a,b]</math>. אזי f אינטגרבילית ב-<math>[a,b]</math>. | ||
===הוכחה=== | ===הוכחה=== | ||
| − | נוכיח לפונקציה עולה. לכל <math>x\in[a,b]</math> מתקיים <math>f(a)\le f(x)\le f(b)</math> ולכן f חסומה. כעת ניקח חלוקה P כלשהי של <math>[a,b]</math> | + | נוכיח לפונקציה עולה. לכל <math>x\in[a,b]</math> מתקיים <math>f(a)\le f(x)\le f(b)</math> ולכן f חסומה. כעת ניקח חלוקה <math>P=\{x_0,\dots,x_n\}</math> כלשהי של <math>[a,b]</math> המקיימת לכל k, <math>\Delta x_k=\frac{b-a}n</math> (ובפרט הם שווים) אזי <math>\overline S(f,P)-\underline S(f,P)=\sum_{k=1}^n(M_k-m_k)\Delta x_k=\sum_{k=1}^n\Big(f(x_k)-f(x_{k-1})\Big)\Delta x_k</math>. |
| − | + | מכאן נובע כי | |
| − | + | ||
| − | + | ||
{{left|<math>\begin{align}\overline S(f,P)-\underline S(f,P)&=\frac{b-a}n\sum_{k=1}^n\Big(f(x_k)-f(x_{k-1})\Big)\\&=\frac{b-a}n\sum_{k=1}^n\Big(f(x_1)-\underbrace{f(x_0)}_{=f(a)}+f(x_2)-f(x_1)+\dots+\underbrace{f(x_n)}_{=f(b)}+f(x_{n-1})\Big)\\&=\frac{b-a}n\Big(f(b)-f(a)\Big)\end{align}</math>}} | {{left|<math>\begin{align}\overline S(f,P)-\underline S(f,P)&=\frac{b-a}n\sum_{k=1}^n\Big(f(x_k)-f(x_{k-1})\Big)\\&=\frac{b-a}n\sum_{k=1}^n\Big(f(x_1)-\underbrace{f(x_0)}_{=f(a)}+f(x_2)-f(x_1)+\dots+\underbrace{f(x_n)}_{=f(b)}+f(x_{n-1})\Big)\\&=\frac{b-a}n\Big(f(b)-f(a)\Big)\end{align}</math>}} | ||
נשאיף <math>n\to\infty</math> ואגף ימין שואף ל-0. מכאן ש-<math>\overline S(f,P)-\underline S(f,P)</math> קטן כרצוננו, וקיימנו את התנאי של משפט 5. לכן f אינטגרבילית ב-<math>[a,b]</math>. {{משל}} | נשאיף <math>n\to\infty</math> ואגף ימין שואף ל-0. מכאן ש-<math>\overline S(f,P)-\underline S(f,P)</math> קטן כרצוננו, וקיימנו את התנאי של משפט 5. לכן f אינטגרבילית ב-<math>[a,b]</math>. {{משל}} | ||
גרסה אחרונה מ־20:29, 29 ביולי 2012
את משפט 2 לא סיימנו בשיעור הקודם ולכן השלמנו זאת ב־22.2.11. חלק זה מופיע בסיכום השיעור הקודם ולא בדף הנוכחי.
תוכן עניינים
האינטגרל לפי דרבו (המשך)
משפט 3
תהי f מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי
. אזי 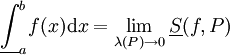 וכן
וכן 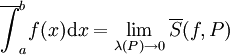 .
.
הוכחה
הטענה הראשונה אומרת שלכל  קיים
קיים 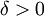 כך שאם
כך שאם 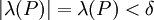 אזי
אזי 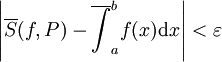 . ברור מהגדרת האינטגרל העליון כי
. ברור מהגדרת האינטגרל העליון כי 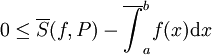 . כעת יהי
. כעת יהי  נתון. לפי הגדרת האינפימום קיימת חלוקה מסויימת Q של
נתון. לפי הגדרת האינפימום קיימת חלוקה מסויימת Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-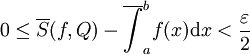 ונניח של-Q יש r נקודות חלוקה. כעת נניח ש-P חלוקה כלשהי של
ונניח של-Q יש r נקודות חלוקה. כעת נניח ש-P חלוקה כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-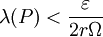 , ונגדיר
, ונגדיר 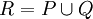 . כיוון ש-R עידון של Q,
. כיוון ש-R עידון של Q, 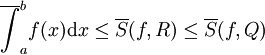 ונובע ש-
ונובע ש-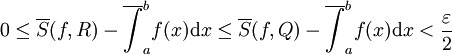 . אבל R התקבלה מ-P ע"י הוספה של לכל היותר r נקודות, לכן ע"פ משפט 2 ידוע ש-
. אבל R התקבלה מ-P ע"י הוספה של לכל היותר r נקודות, לכן ע"פ משפט 2 ידוע ש-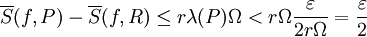 . לכן נוכל להסיק
. לכן נוכל להסיק
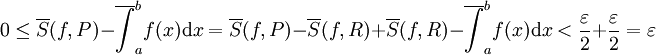 .
.
ההוכחה לאינטגרל התחתון דומה. 
משפט 4
תהי f כנ"ל. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם"ם
אם"ם 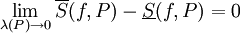 ואם כן
ואם כן 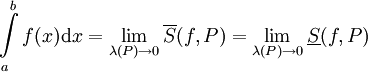 .
.
הוכחה
תחילה נניח ש-f אינטגרבילית, ז"א 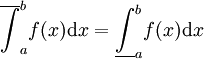 . לכן, ממשפט 3,
. לכן, ממשפט 3, 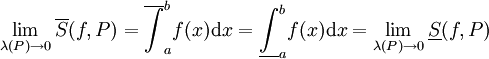 . ע"פ אריתמטיקה של גבולות
. ע"פ אריתמטיקה של גבולות 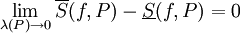 וכן
וכן 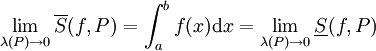 .
.
עכשיו נניח ש-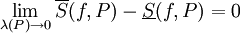 ונוכיח את ההיפך. ממשפט 3
ונוכיח את ההיפך. ממשפט 3 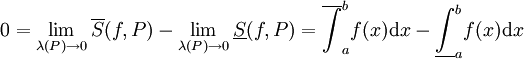 ולכן f אינטגרבילית.
ולכן f אינטגרבילית. 
משפט 5
תהי f כנ"ל. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם"ם לכל
אם"ם לכל  קיימת חלוקה P של
קיימת חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-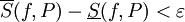 .
.
הוכחה
אם נתון ש-f אינטגרבילית אז ממשפט 4 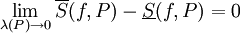 . לכן עבור
. לכן עבור  קיים
קיים 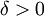 כך שלכל P המקיימת
כך שלכל P המקיימת 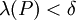 מתקיים
מתקיים 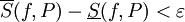 .
.
לצד השני, נניח שלכל  קיימת חלוקה P כך שמתקיים
קיימת חלוקה P כך שמתקיים 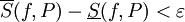 . כידוע, לכל חלוקה P מתקיים
. כידוע, לכל חלוקה P מתקיים 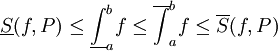 . לפי הנתון נקבל
. לפי הנתון נקבל 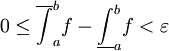 . זה נכון לכל
. זה נכון לכל  ולכן
ולכן 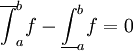 , כלומר f אינטגרבילית ב-
, כלומר f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 
משפט 6
תהי f רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
יהי  . כיוון ש-f רציפה בקטע סגור
. כיוון ש-f רציפה בקטע סגור ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) היא רציפה במ"ש, לכן קיים
היא רציפה במ"ש, לכן קיים 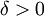 כך שאם
כך שאם ![x_1,x_2\in[a,b]](/images/math/7/9/6/796b580b3cc8423dee93c2c4cda68438.png) ו-
ו-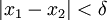 אז
אז 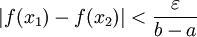 . כעת תהי P חלוקה כלשהי של
. כעת תהי P חלוקה כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך ש-
כך ש-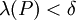 . לפיכך
. לפיכך 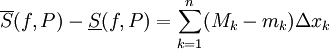 כאשר
כאשר 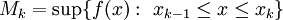 ו-
ו-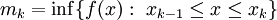 . כיוון ש-f רציפה ושעפ"י המשפט השני של ויירשראס לכל f רציפה ב-
. כיוון ש-f רציפה ושעפ"י המשפט השני של ויירשראס לכל f רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) יש שם נקודות מינימום ומקסימום, לכל k קיימים
יש שם נקודות מינימום ומקסימום, לכל k קיימים ![y_k,z_k\in[x_{k-1},x_k]](/images/math/5/b/1/5b139ea3a75ba891882b90f1eae3ee92.png) כך ש-
כך ש-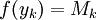 ו-
ו-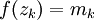 . כעת
. כעת 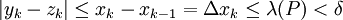 , לכן
, לכן 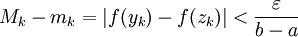 ולבסוף
ולבסוף
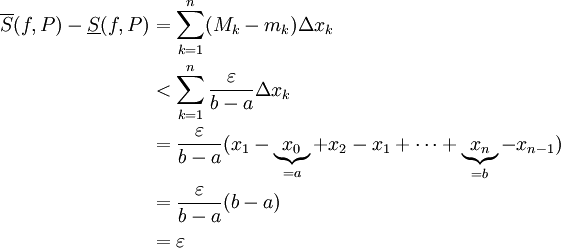
ונובע ממשפט 5 (או 4) ש-f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 
משפט 7
תהי f מוגדרת ומונוטונית בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
נוכיח לפונקציה עולה. לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) מתקיים
מתקיים 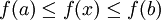 ולכן f חסומה. כעת ניקח חלוקה
ולכן f חסומה. כעת ניקח חלוקה 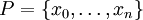 כלשהי של
כלשהי של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) המקיימת לכל k,
המקיימת לכל k, 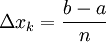 (ובפרט הם שווים) אזי
(ובפרט הם שווים) אזי 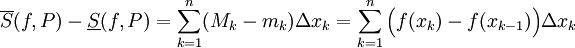 .
.
מכאן נובע כי
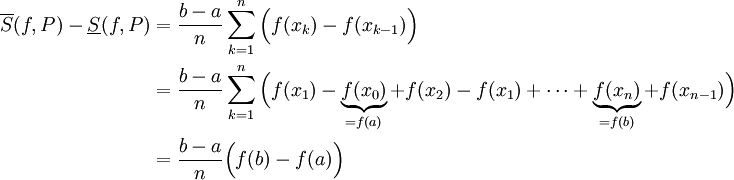
נשאיף 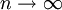 ואגף ימין שואף ל-0. מכאן ש-
ואגף ימין שואף ל-0. מכאן ש-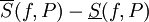 קטן כרצוננו, וקיימנו את התנאי של משפט 5. לכן f אינטגרבילית ב-
קטן כרצוננו, וקיימנו את התנאי של משפט 5. לכן f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 