בדידה לתיכוניסטים תש"ע - שאלות ותשובות

[math]\displaystyle{ {n \choose k} = {n!\over k!(n-k)!} }[/math]

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:

== כותרת לשאלה ==

לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין

ארכיון

ארכיון 1 - יהיה בהמשך

שאלות

שאלה 10

[math]\displaystyle{ \{(x,y)\in \mathbb{R}^2:|x|,|y|\le 1\} \setminus \{(x,y)\in \mathbb{R}^2:x^2+y^2\le 1\} }[/math]

מישהו יכול לתת לי כיוון כללי איך צריך לפתור את השאלה הזאת,להסביר אותה..?

נראה לי שהכוונה היא פשוט למצוא 2 קבוצות מסוימות A ו B שהמכפלה הקרטזית שלהם תיצור את הקבוצות שבסעיפים.

ככה שהX יהיה שייך לA וY לB?

בסעיף א' נגיד, (נראה לי, אני לא בטוח לגמרי) התשובה היא ש A היא כל הXים וB היא כל הYים. (או A הוא הקו (1,1) וגם B הוא הקו (1,1).) תקנו אותי אם אני טועה בבקשה!

כמו שאמר זה שמעליי, צריך למצוא 2 קבוצות A ו-B שהמכפלה הקרטזית שלהן תהיה שווה לקבוצה הנתונה.

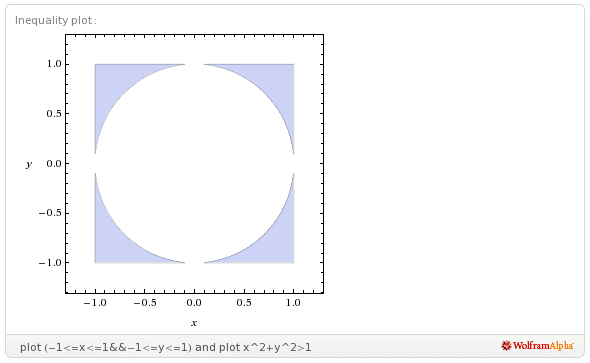
לדוגמא סעיף א': [math]\displaystyle{ A\times B=\{(x,y) \in \mathbb{R} \times \mathbb{R}| x^2+y^2\le1 \} }[/math] אז בעצם זה שפת המעגל הקנוני רדיוסו 1 וכל פנים המעגל. לכן (0,1) יקיים וגם (1,0) יקיים, אך מכך נובע ש-[math]\displaystyle{ 1\in A\wedge 1\in B }[/math] אז גם (1,1) אמור לקיים אך הוא לא, אז לא קיימים A ו-B עבורם מתקיים: [math]\displaystyle{ A\times B=\{(x,y) \in \mathbb{R} \times \mathbb{R}| x^2+y^2\le1 \} }[/math] תומר זוארץ 20:49, 25 ביולי 2010 (IDT)

הוספתי לאחר התנגשות עריכה - במישור הקרטזי הדו-מימדי, במכפלה [math]\displaystyle{ A \times B }[/math] איברי A יוצרים את שיעורי ה-x ואיברי B יוצרים את שיעורי ה-y, ולכן המכפלה יוצרת מלבן (אם [math]\displaystyle{ |A|,|B| \gt 1 }[/math]) או קטע ([math]\displaystyle{ |A| = 1 \veebar |B| = 1 }[/math]) או נקודה ([math]\displaystyle{ |A| = |B| = 1 }[/math]) (או כמה מלבנים/קטעים/נקודות, אם האיברים ב-A או (מכליל) B לא יוצרים רצף על ציר המספרים, כלומר קיים איבר y כך שעבור [math]\displaystyle{ S=A \veebar S=B }[/math] מתקיים: [math]\displaystyle{ x,z \in S \and x\lt y\lt z }[/math] אבל [math]\displaystyle{ y\not\in S }[/math]) לכל [math]\displaystyle{ A,B\not= \empty }[/math]. הקבוצה הנתונה בסעיף א' היא עיגול היחידה. זה אמור לתת לך רעיון איך לפתור את זה. -אור שחף, שיחה, 20:57, 25 ביולי 2010 (IDT)

יחס שקילות וחלוקה

הנושא הזה לא כל כך ברור לי, האם מישהו יכול להסביר איך חלוקה יוצרת יחס ? והיחס פועל בתוך [math]\displaystyle{ {Ai} }[/math] או בתוך כל קבוצה [math]\displaystyle{ A }[/math] ? תודה מראש, חופית

אם את מחלקת קבוצה נתונה לאוסף תת-קבוצות זרות כשהאיחוד של כולן נותן את הקבוצה המקורית אז החלוקה הזו משרה יחס שקילות. מהו יחס השקילות שהיא משרה? יחס השקילות שהחלוקה משרה הוא שכל שני איברים שקולים אם ורק אם הם שייכים לאותה תת-קבוצה בחלוקה. דוגמא: ניקח את הקבוצה [math]\displaystyle{ A=\left{1,2,3,4\right} }[/math] ונביט בחלוקה [math]\displaystyle{ A_1={1} }[/math], [math]\displaystyle{ A_2={2,3} }[/math], [math]\displaystyle{ A_3={4} }[/math]. יחס השקילות שהחלוקה משרה הוא [math]\displaystyle{ R={(1,1),(2,2),(3,3),(4,4),(2,3),(3,2)} }[/math]. Adam Chapman 23:04, 25 ביולי 2010 (IDT)

שאלה 8- נתונים *לא נפתר-עזרה בבקשה*

בשאלה 8 מגדירים חוג מעל X. האם זו הגדרה של משהו שנלמד או הגדרה שרירותית כלשהי שהמציאו בשביל התרגיל? כלומר האם כל הנתונים באמת רלוונטיים לתרגיל עצמו? אני הצלחתי אותו כשהשתמשתי רק בנתונים שמופיעים בסעיף א' ו- ג'. (וגם את א' לא הייתי בטוח אם לכתוב כאן...)

חוג זה אכן אובייקט ש(למיטב ידיעתי) לא למדתם בכיתה (לא בהרצאה ולא בתרגיל). לכן ההגדרה המדוייקת שלו מופיעה בשאלה (אובייקט שנלמד בכיתה, כמו למשל קבוצת החזקה, לא מוגדר במלואו בתרגיל). זה חלק מהתרגיל, שתתרגלו קריאת הגדרות של אובייקטים חדשים שלא הכרתם קודם ופיתרון בעיות הקשורות באובייקטים האלה ע"י שימוש נכון בהגדרת האובייקט. זה גם נכון שעל אף שאנחנו נותנים לכם את ההגדרה המלאה והמדוייקת של האובייקט, זה לא אומר שבכל אחת מן התכונות חייבים להשתמש כדי להוכיח את מה שאתם נדרשים בשאלה. Adam Chapman 23:13, 23 ביולי 2010 (IDT)

מישהו יכול להסביר איך בכלל לפתור את שאלה 8?

מצטרף לשאלה, שאלה 8 היא השאלה היחידה שעדיין לא הצלחתי לפתור. אני פשוט לא יודע איך להוכיח את מה שצריך להוכיח בעזרת הנתונים. אפשר רמז? תודה רבה. (ערכתי את הנושא כך שידעו שצריך פה עזרה).

ה- R בשאלה 10

האם ה- R בשאלה 10 הוא קבוצת הממשיים?

ה-R בשאלה 10 הוא אכן המספרים הממשיים, כיוון ש:

א. גם בשאלה 6 ה-R של הממשיים מופיע ללא קו.

ב. לא יכול להיות ש-R הוא יחס מ-A ל-B וגם [math]\displaystyle{ A,B\subseteq R }[/math]

בשאלה 10 R הוא אכן קבוצת הממשיים (או שדה הממשיים, למי שרוצה קצת להיזכר בחומר של אלגברה ליניארית). זה נכון שכעיקרון הוא צריך להיות מסומן ב[math]\displaystyle{ \mathbb{R} }[/math], אך כנראה שבפורמט הספציפי שבו נכתבה השאלה היה קושי לסמנו כך ולכן הוא נשאר פשוט R. איתכם הסליחה על הבלבול בסימנים. בכל-זאת, אתם מתבקשים להקפיד על הסימון של קבוצת הממשיים כ[math]\displaystyle{ \mathbb{R} }[/math] ולא כפשוט R, כדי שגם אנחנו נבין את מה שאתם כותבים יותר טוב. Adam Chapman 23:23, 23 ביולי 2010 (IDT)

שאלה כלילת- מכפלה קרטזית בקבוצה ריקה

כאשר כופלים קבוצה כלשהי שאינה קבוצה ריקה במכפלה קרטזית בקבוצה ריקה האם הקבוצה המתקבלת היא קבוצה ריקה?

תשובה לעצמי: כן

שאלות 7(ו,ז), 8, 9 ו10

אני לא יודע איך פותרים את שאלות 7(ו,ז), 8, 9 ו10. כשהיה צריך לעשות הוכחות עם חיתוך,איחוד והפרש של קבוצות, הצלחתי, אבל אני פשוט לא יודע איך "לטפל" בשאלות עם קבוצת חזקה וכו'. עזרה בבקשה!

השאלה היא האם אתה יודע מה היא ההגדרה של קבוצה החזקה, משום שברגע שאתה מבין היטב מה היא ההגדרה אז מכאן ואילך לא אמורות להיות בעיות, במיוחד אם אתה שולט היטב כבר בחיתוך\איחוד. בו נראה - קבוצה החזקה של [math]\displaystyle{ A }[/math] היא קבוצת כל תת-הקבוצות של [math]\displaystyle{ A }[/math], דהיינו [math]\displaystyle{ x \in P(A) }[/math] אם ורק אם [math]\displaystyle{ x \subseteq A }[/math]. במילים, איבר שייך לקבוצת החזקה של [math]\displaystyle{ A }[/math] אם ורק אם הוא תת-קבוצה של [math]\displaystyle{ A }[/math]. המלצה שלי היא שתנסה לנסח את השאלות שאתה מתבקש לענות עליהן כתרגיל בלי להשתמש במונח\סימן של קבוצת החזקה אלא בהגדרה שעומדת מאחוריה. Adam Chapman 15:30, 23 ביולי 2010 (IDT)

שאלה 9

אם אני צריכה להוכיח שמשהו מוכל ממש במשהו אחר, והוכחתי שזה מול או שווה, ובנוסף, מצאתי דוגמא לכך שזה שווה. זה נחשב הוכחה או הפרכה?

נראה לי שהכוונה ב"מוכל ממש" (גם לפי הסימן) היא שקבוצה אחת מוכלת בקבוצה שנייה אבל לא שווה לה. לכן את צריכה להוכיח שקבוצה אחת מוכלת בשנייה, וגם להוכיח שהיא לא שווה לה. אם תוכיחי את זה, זאת תהיה הוכחה (לא הפרכה). את יכולה להסביר איך הצלחת להוכיח את ההכלה בשאלה 9? תודה

אכן זו הכוונה. אם מצאת מקרה של שוויון אזי הדבר מהווה הפרכה, כי הרי אסור שזה יהיה שווה. במקרה כזה את אפילו לא צריכה להראות שזה מוכל או שווה, אלא פשוט לתת את מקרה השוויון כדוגמה נגדית ולומר שמשום כך הטענה לא מתקיימת...

הוכחה

האם חובה להוכיח ש-[math]\displaystyle{ \overline{\bigcup_{i \in I} A_i } = \bigcap_{i \in I} \overline{A_i} }[/math] ולהיפך (עם חיתוך במקום איחוד) במבחנים ובש"ב? תודה, אור שחף - שיחה 19:33, 20 ביולי 2010 (UTC)

אור, זה בעצם חוקי דה-מורגן שלכל [math]\displaystyle{ (A_i\cup A_{i+1})^c = A_i^c\cap A_{i+1}^c }[/math] רק באופן כללי וגורף [math]\displaystyle{ \forall i\in I }[/math], באיחוד מלא. בחוקי דה-מורגן אפשר להשתמש ללא הוכחה.. אך עדיין אני לא בטוח ב-100%.. חוקי דה-מורגן באיחוד מלא..

הבעיה היא לא איך, אלא האם. הוכחה שלמה יכולה להיות די ארוכה (עם אינדוקציה, למשל, ומה שרשמת), ואני לא אכתוב את כל זה סתם. בינתיים אני משאיר את זה בלי הוכחה, אם מישהו יודע שצריך להוכיח - שיגיב. תודה, אור שחף - שיחה 12:02, 21 ביולי 2010 (UTC)

חברים שלי הלכו לשעות הקבלה של המרצה שי סרוסי והוא הסביר שצריך להוכיח את זה באינדוקציה(גם אני עשיתי כמוך וחברים שלי הראו לו את ההוכחה הזאת)

כן, אבל השאלה היא לא איך להוכיח את זה (במקרה כזה מוכיחים כמובן באינדוקציה, זו הדרך הכי טריוויאלית שיש) אלא האם יש צורך להוכיח את זה כל פעם מחדש. האם מישהו שאל את המתרגל שלו ויכול לענות על השאלה?

שים לב כתבתי שהוא אמר שצריך כלומר חייב להוכיח את זה כל פעם מחדש עפ"י דבריו.

אוקי. בכל אופן - האם אחד מהמתרגלים יכול להבהיר נקודה זו?

שאלה 4

בסעיף ג' הניסוח של השאלה לא ברור לי. צריך להוכיח שהאיחוד של כל הקבוצות Ai פחות החיתוך של כל הקבוצות Bj שווה למה? תודה מראש, דניאל.

שווה ל-[math]\displaystyle{ \begin{align} \bigcup_{i=1}^n \big((A_i - B_1) \cup (A_i - B_2) \cup (A_i - B_3) \cup \dots \cup (A_i - B_m)\big) \\ = \big((A_1 - B_1) \cup (A_1 - B_2) \cup \dots \cup (A_1 - B_m)\big) \cup \big((A_2 - B_1) \cup \dots \cup (A_2 - B_m)\big) \cup \dots \cup \big((A_n - B_1) \cup \dots \cup (A_n - B_m)\big) \end{align} }[/math]

אור שחף - שיחה 18:19, 20 ביולי 2010 (UTC)

שאלה 3

מי הצליח להוכיח את שאלה 3ב.?

אני, ואל תצפה להוכחה פשוטה. אחרי שהוכחתי את זה בדרך המסובכת, חיפשתי בגוגל הוכחות יותר טובות, אבל כל האתרים מוכיחים את זה בצורה דומה. נ.ב. כדאי לכתוב שאלות חדשות בראש העמוד, ככה כולם עשו עד עכשיו (ולכן, אם תכתוב שאלה בתחתית אף אחד לא יראה אותה). אור שחף - שיחה 15:45, 20 ביולי 2010 (UTC)

תרגיל 6

האם אני צריכה להוכיח שהקבוצות שבחרתי Bi מקיימות את התנאים הדרושים? תודה, חן.

כן. תמיד בתשובות במתמטיקה יש לנמק, לא מספיק לתת תשובה סופית

תרגיל 1.ב

בתרגיל 1, סעיף ב, האם צריך להוכיח ש-[math]\displaystyle{ \mathbb{Q} \subset \mathbb{R} }[/math]? ובמבחנים? תודה, אור שחף 11:26, 20 ביולי 2010 (UTC)

אור, אני לא מתרגל ו/או מרצה בקורס זה (אלא תלמיד סה"כ) ולכן אל תיקח את התשובה שלי כתשובה שאתה יכול להסתמך עליה. עם זאת, נראה לי שהדבר טרוויאלי ונובע ישירות מההגדרה של קבוצות אלו, ולכן אין צורך להוכיח את זה במבחן, אלא רק לציין שהדבר מתקיים אם אתה צריך לעשות בו שימוש.

תרגיל 1,שאלה 6

לא הצלחתי להבין מה מבקשים בשאלה 6, מה זאת אומרת "הצג..."?

אני חושב שאת/ה צריך/ה לת דוגמה. אור שחף 11:26, 20 ביולי 2010 (UTC)

קבוצות מוכלות זו בזו

שלום לכולם, האם נכון לומר שבמידה וקבוצה [math]\displaystyle{ A }[/math] מוכלת בקבוצה [math]\displaystyle{ B }[/math] אז [math]\displaystyle{ \mathcal{P}(A) }[/math] תהיה מוכלת ב-[math]\displaystyle{ \mathcal{P}(B) }[/math]? תודה שוב, גל.

תשובה

תחשוב על ההגדרות ועל מה זה אומר ש-X שייך ל- [math]\displaystyle{ \mathcal{P}(A) }[/math] והאם בהכרח הוא שייך ל [math]\displaystyle{ \mathcal{P}(B) }[/math]

חידוד השאלה בנושא זה

לא כל כך הבנתי את התשובה שלך. כמובן שלפני שאני שולח כאן אני מסתכל על הגדרות, ולכן אחדד את שאלתי (יש לי תחושה שלא הובנתי נכון): נניח שנתון לי ש-[math]\displaystyle{ X }[/math] כלשהו שייך לקבוצה [math]\displaystyle{ A }[/math] ושאותה קבוצה [math]\displaystyle{ A }[/math] מוכלת בקבוצה [math]\displaystyle{ B }[/math] כלשהי. לכן האיבר [math]\displaystyle{ X }[/math] הינו איבר גם בקבוצה [math]\displaystyle{ B }[/math]. משום כך {X} הוא איבר ב- [math]\displaystyle{ P(A) }[/math] וגם ב- [math]\displaystyle{ P(B) }[/math]. האם מכאן אני יכול לקבוע שהקבוצה [math]\displaystyle{ P(A) }[/math] מוכלת בקבוצה [math]\displaystyle{ P(B) }[/math] (נראה לי שהתשובה היא כן אבל אני רוצה להיות בטוח)? והאם אני יכול להשתמש בזה בהוכחות בלי צורך להוכיח את זה כל פעם מחדש (או פשוט לומר ישירות שמכיוון שמתקיים [math]\displaystyle{ A \subset \ B }[/math] אז [math]\displaystyle{ P(A) \subset \ P(B) }[/math])? תודה, גל.

אנחנו מכוונים אותך להגדרות לא כי אנחנו חושבים שלא קראת לבד קודם, אלא כי חשוב לדעת להוכיח מתמטיקה במדויק לפי ההגדרות. מתי אנחנו יודעים שA מוכלת בB לפי הגדרה? אם אתה רוצה לטעון ש[math]\displaystyle{ P(A) \subset \ P(B) }[/math] תוכיח את זה במדויק לפי ההגדרה.

מה שעשית למעלה הוא הסבר עם דוגמא אבל לא הוכחה שלימה.--ארז שיינר 11:57, 20 ביולי 2010 (UTC)

ברור לי גם שעליי להוסיף להוכחה את העובדה שב- [math]\displaystyle{ P(B) }[/math] יש איבר שאין אותו ב- [math]\displaystyle{ P(A) }[/math]. וסליחה על השאלה הקצת טיפשית, מה עליי להוסיף בכדי שהדבר ייחשב להוכחה שלמה?

הוספתי לאחר התנגשות עריכה - הוכחה: תהי קבוצה X כך ש-[math]\displaystyle{ X \in \mathcal{P}(A) }[/math]. לפיכך [math]\displaystyle{ X \in \left\{S|S \subseteq A\right\} }[/math]. מתקיים [math]\displaystyle{ A \subseteq B }[/math] ולכן [math]\displaystyle{ \left\{S|S \subseteq A\right\} \subseteq \left\{S|S \subseteq B\right\} \Rightarrow \left\{X\right\} \subseteq \left\{S|S \subseteq B\right\} = \mathcal{P}(B) }[/math] ולבסוף: [math]\displaystyle{ X \in \mathcal{P}(B) }[/math]. מכאן נובעת הטענה המתבקשת, מש"ל. אור שחף 12:10, 20 ביולי 2010 (UTC)

עכשיו הבנתי. האם אני צריך להציג את זה בכל מקום שאני מסתמך על כך או שלא? תודה גל.

אתה מתכוון במבחנים ובתרגילים? אני מנחש שלא, אבל עדיף לשאול את המרצים ב-google groups. אור שחף - שיחה 12:24, 20 ביולי 2010 (UTC):

שאלתי את המתרגלת שלי והיא אמרה שלא צריך...

תרגיל 1

שלום רב, היום העלתם את התרגיל הראשון, אך לא כתבתם תאריך הגשה. מתי צריך להגיש אותו? תודה, גל.

שלום גל, לפי מה שידוע לי צריך להגיש ביום רביעי 28.7. אלה.