עקיפה של אור: הבדלים בין גרסאות בדף
(יצירת דף עם התוכן "ניסוי עקיפה מסדקים בוצע ב-1801, על ידי הפיזיקאי תומאס יאנג, על מנת להכריע האם האור הוא גל או...") |
|||
| שורה 9: | שורה 9: | ||
<math>Y_1=A_1 \sin (\omega t+\theta_1)</math> | <math>Y_1=A_1 \sin (\omega t+\theta_1)</math> | ||
<math>Y_2=A_2 \sin (\omega t+\theta_2)</math> | |||
<math>A_1,A_2</math> אמפליטודת הגלים, <math>\omega</math> המהירות הזויתית ו-<math>\theta_1, \theta_2</math> הפאזות ההתחלתיות של הגלים. | |||
לפי עקרון הסופר פוזיציה התנועה השקולה באותה נקודה נראית כמו: | |||
<math>Y_1+Y_2=A_1 \sin (\omega t+\theta_1)+A_2 \sin (\omega t+\theta_2)</math> | |||
* עבור <math>\Delta\theta=\theta_1-theta_2=0</math> נקבל <math>A=A_1+A_2</math> . כלומר, האמפליטודה השקולה שווה לסכום האמפליטודה של המרכיבים (התאבכות בונה). | |||
* עבור <math>\Delta\theta=\theta_1-theta_2=\pi</math> נקבל <math>A=A_1-A_2</math> . כלומר, האמפליטודה השקולה שווה להפרש האמפליטודה של המרכיבים (התאבכות הורסת). | |||
במקרה מיוחד של התאבכות הורסת, כאשר שתי האמפליטודות שוות, נקבל מקרה בו <math>A=0</math> , כלומר בנקודה לא יהיה אור. | |||
ידוע שעוצמת הגל <math>I</math> פרופורציוניות לריבוע האמפליטודה, לכן במקרה הספציפי בו <math>A_1=A_2</math> נקבל : | |||
<math>I=A^2={A_1}^2\cos({\Delta \theta} \over 2) </math> | |||
כלומר עוצמת הגל (האור) הנוצרת בסופרפוזיציה של שני גלים בעלי תדירות שווה תלויה בהפרש הפאזות בין הגלים הנפגשים. | |||
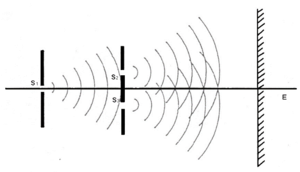
[[קובץ:התאבכות.png|300px|שמאל|ממוזער|איור 1 - התאבכות משני סדקים]] | |||
בניסוי של התאבכות משני סדקים משתמשים במקור אור אחד העובר דרך שני סדקים דקים הרחוקים מרחק <math>d</math> ביניהם. בצורה כזו ניתן לקבל שני מקורות אור קוהרנטים (ללא הפרש פאזה ביניהם), ראו איור 1. | |||
גרסה מ־15:47, 23 באוקטובר 2014
ניסוי עקיפה מסדקים בוצע ב-1801, על ידי הפיזיקאי תומאס יאנג, על מנת להכריע האם האור הוא גל או חלקיק. בניסוי, התקבלה התנהגות גלית של האור (התאבכות ועקיפה), ובעקבות כך, במשך כל המאה ה-19, עד לניסוי פרנק-הרץ והמאמר על האפקט הפוטואלקטרי של אלברט איינשטיין, ההנחה המקובלת הייתה שהאור הוא גל. בניסוי זה נמדוד את עצמת האור הנפלט מלייזר חצי מוליך, לאחר מעבר האלומה דרך סדק בודד, שני סדקים ושריג עקיפה. בנוסף, נמדוד את התופעה ההפוכה בה מתרחשת עקיפה לאחר מעבר אלומת האור מחסומים דקים. באמצעות תבניות העקיפה וההתאבכות המתקבלות נמצא את אורך הגל של קרינת הליזר ואת וחב המחסומים אותם עבר האור.
רקע תיאורטי
האור הנראה יכול להיות מתואר על ידי תנועה של גלים אלקטרומגנטים בעלי אורך גל, אמפליטודה ופאזה. ככל גל, מתאפיינים גלי האור בתדירות, [math]\displaystyle{ f }[/math] , משרעת, [math]\displaystyle{ A }[/math], מהירות, [math]\displaystyle{ v }[/math], ואורך גל, [math]\displaystyle{ λ }[/math]. תדירות הגל תלוייה במקור, מהירות הגל תלוייה בתווך בו עובר הגל והיחס בינהם הוא התדר [math]\displaystyle{ f=v/λ }[/math]. עקרון הסופרפוזיציה קובע שכאשר בתווך מסוים עוברים מספר גלים בו-זמנית מתקבל גל שקול אשר שווה לסכום הגלים העוברים בתווך. כלומר, כל הגדלים המאפיינים את הגלים מתחברים לפי כללי החיבור הווקטורי. נדון עתה בסופר-פוזיציה (סכימה) של שני גלים הרמונים, בעלי תדירות שווה בנקודה מסוימת של המרחב. נרשום משוואות עבור שני גלים [math]\displaystyle{ Y_1 }[/math] ו-[math]\displaystyle{ Y_2 }[/math] במיקום מסויים:
[math]\displaystyle{ Y_1=A_1 \sin (\omega t+\theta_1) }[/math] [math]\displaystyle{ Y_2=A_2 \sin (\omega t+\theta_2) }[/math]
[math]\displaystyle{ A_1,A_2 }[/math] אמפליטודת הגלים, [math]\displaystyle{ \omega }[/math] המהירות הזויתית ו-[math]\displaystyle{ \theta_1, \theta_2 }[/math] הפאזות ההתחלתיות של הגלים.
לפי עקרון הסופר פוזיציה התנועה השקולה באותה נקודה נראית כמו:
[math]\displaystyle{ Y_1+Y_2=A_1 \sin (\omega t+\theta_1)+A_2 \sin (\omega t+\theta_2) }[/math]
- עבור [math]\displaystyle{ \Delta\theta=\theta_1-theta_2=0 }[/math] נקבל [math]\displaystyle{ A=A_1+A_2 }[/math] . כלומר, האמפליטודה השקולה שווה לסכום האמפליטודה של המרכיבים (התאבכות בונה).
- עבור [math]\displaystyle{ \Delta\theta=\theta_1-theta_2=\pi }[/math] נקבל [math]\displaystyle{ A=A_1-A_2 }[/math] . כלומר, האמפליטודה השקולה שווה להפרש האמפליטודה של המרכיבים (התאבכות הורסת).
במקרה מיוחד של התאבכות הורסת, כאשר שתי האמפליטודות שוות, נקבל מקרה בו [math]\displaystyle{ A=0 }[/math] , כלומר בנקודה לא יהיה אור.
ידוע שעוצמת הגל [math]\displaystyle{ I }[/math] פרופורציוניות לריבוע האמפליטודה, לכן במקרה הספציפי בו [math]\displaystyle{ A_1=A_2 }[/math] נקבל :
[math]\displaystyle{ I=A^2={A_1}^2\cos({\Delta \theta} \over 2) }[/math]
כלומר עוצמת הגל (האור) הנוצרת בסופרפוזיציה של שני גלים בעלי תדירות שווה תלויה בהפרש הפאזות בין הגלים הנפגשים.
בניסוי של התאבכות משני סדקים משתמשים במקור אור אחד העובר דרך שני סדקים דקים הרחוקים מרחק [math]\displaystyle{ d }[/math] ביניהם. בצורה כזו ניתן לקבל שני מקורות אור קוהרנטים (ללא הפרש פאזה ביניהם), ראו איור 1.