מכינה למחלקת מתמטיקה/מערכי שיעור/3: הבדלים בין גרסאות בדף
אין תקציר עריכה |
|||
| שורה 23: | שורה 23: | ||
*<math>cot(t):= \frac{cos(t)}{sin(t)}=\frac{1}{tan(t)}</math> | *<math>cot(t):= \frac{cos(t)}{sin(t)}=\frac{1}{tan(t)}</math> | ||
==זהויות טריגונומטריות== | |||
ישנן זהויות טריגונומטריות רבות, ניתן לעיין ברשימה מלאה למדי ב[http://he.wikipedia.org/wiki/%D7%96%D7%94%D7%95%D7%99%D7%95%D7%AA_%D7%98%D7%A8%D7%99%D7%92%D7%95%D7%A0%D7%95%D7%9E%D7%98%D7%A8%D7%99%D7%95%D7%AA ויקיפדיה]. בשיעור זה נזכיר חלק מן הזהויות הבסיסיות. | |||
גרסה מ־00:44, 6 באוגוסט 2012
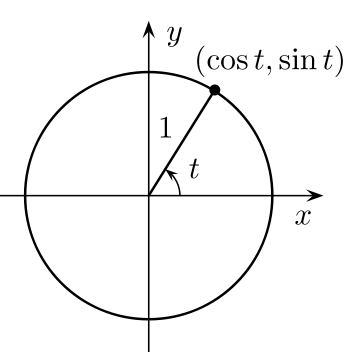
הגדרת הפונקציות הטריגונומטריות באמצעות מעגל היחידה
במעגל ישנן 360 מעלות השקולות ל[math]\displaystyle{ 2\pi }[/math] רדיאנים, וידוע כי היקף מעגל עם רדיוס r הינו [math]\displaystyle{ 2\pi r }[/math]. בלימודי המתמטיקה נשתמש בלבד בשיטת הרדיאנים לפיה הזוית בין שני ישרים היא אורך קטע הקשת שהם פורסים ממעגל היחידה (כלומר, מעגל עם רדיוס אחד שמרכזו בראשית הצירים).
נגדיר את הפונקציות הטריגונומטריות באמצעות מעגל היחידה.
- [math]\displaystyle{ sin(t) }[/math] מוגדר להיות ערך ציר ה-[math]\displaystyle{ y }[/math] של הנקודה על מעגל היחידה הממוקמת במרחק של [math]\displaystyle{ t }[/math] סיבובים כנגד כיוון השעון (תחילת הסיבובים בנקודה [math]\displaystyle{ (1,0) }[/math])
- [math]\displaystyle{ cos(t) }[/math] מוגדר להיות ערך ציר ה-[math]\displaystyle{ x }[/math] של הנקודה על מעגל היחידה הממוקמת במרחק של [math]\displaystyle{ t }[/math] סיבובים כנגד כיוון השעון (תחילת הסיבובים בנקודה [math]\displaystyle{ (1,0) }[/math])
- [math]\displaystyle{ tan(t):=\frac{sin(t)}{cos(t)} }[/math]
- [math]\displaystyle{ cot(t):= \frac{cos(t)}{sin(t)}=\frac{1}{tan(t)} }[/math]
זהויות טריגונומטריות
ישנן זהויות טריגונומטריות רבות, ניתן לעיין ברשימה מלאה למדי בויקיפדיה. בשיעור זה נזכיר חלק מן הזהויות הבסיסיות.