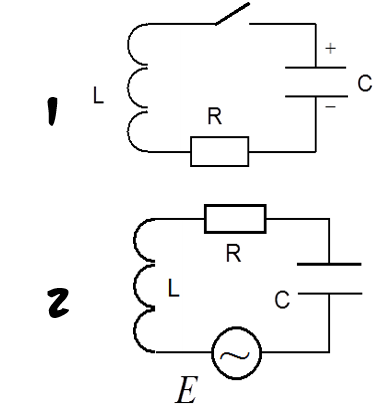מעגל RLC

מעגל [math]\displaystyle{ RLC }[/math] מורכב מנגד [math]\displaystyle{ R }[/math], משרן [math]\displaystyle{ L }[/math] וקבל [math]\displaystyle{ C }[/math]. רכיבים אלו מחוברים בטור או במקביל ספק זרם או מתח. הזרם במעגלי [math]\displaystyle{ RLC }[/math] מתואר על ידי משוואה דפרנציאלית מסדר שני, ולכן יש הקוראים למעגלים אלו מעגלים מסדר שני. באלקטרוניקה משתמשים במעגלי [math]\displaystyle{ RLC }[/math] כמסננים המעבירים רוחבי פס מסוימים של אותות בגלל תופעת התהודה שבהם וכמנחיתי תדרים לא רצויים. אחד השימושים במעגל [math]\displaystyle{ RLC }[/math] הוא בתקשורת רדיו. בניסוי זה נבחן תנודות ותהליכי מעבר של הזרם במעגל, ונכיר את השימוש במעגל כמסנן באמצעות תהודה. ניסוי זה מקביל במהותו לתנודות המכניות במעבדה "תנודות".

רקע תיאורטי

תנודות חופשיות

איור 1-1 מתאר זרם המנודד בתנודות חופשיות בהנחה שהקבל טעון במטען [math]\displaystyle{ Q }[/math]. כאשר נסגור את המפסק [math]\displaystyle{ S }[/math] במעגל סכום המתחים במסלול סגור צריך להיות שווה לאפס- (לפי כלל המתחים של קירכהוף, Kirchhoff), ולכן נקבל:

[math]\displaystyle{ IR+U_C+Lֹ{dI \over dt}=0 }[/math]

איור 1 - מעגל RLC: תנודות חופשיות (1) תנודות מאולצות (2)

כאשר [math]\displaystyle{ I }[/math] הוא הזרם במעגל, [math]\displaystyle{ U_C }[/math] הוא המתח על הקבל, ו- [math]\displaystyle{ -Lֹ{dI \over dt}=0 }[/math] הוא המתח הנוצר בסליל ההשראות בשל שינוי הזרם החשמלי דרכו.

נגזור את המשואה ואחרי חישוב הנגזרת נקבל:

[math]\displaystyle{ {{d^2I} \over dt^2}+{{RdI} \over {Ldt}}+{I \over {LC}}=0 }[/math]

זוהי משוואה דיפרנציאלית מסדר שני המתארת תנודות דועכות. ופתרונה:

[math]\displaystyle{ x(t) = A\exp (-\delta t)\cos ( \Omega t-\phi)) }[/math]

כאשר [math]\displaystyle{ \Omega }[/math] הוא תדר התנודות העצמיות של המערכת השווה ל-[math]\displaystyle{ \Omega ^2 = \omega_0 ^2- \delta^2 }[/math], [math]\displaystyle{ \omega_0^2 = {1 \over {LC}} }[/math], ו- [math]\displaystyle{ \delta={\R \over 2L} }[/math] הנקרא גורם הריסון.

האמפליטודה A והפאזה [math]\displaystyle{ \phi }[/math] תלויים בתנאי התחלה של המערכת.

היחס [math]\displaystyle{ Q=\omega_0 {L \over R}={1 \over {\omega_0 RC}} }[/math] נקרא גורם האיכות של המעגל והוא מבטא את היחס בין המתח האפקטיבי בסליל או בקבל למתח האפקטיבי בנגד.

תנודות מאולצות ותהליכי מעבר

כשמופעל מתח חיצוני (איור 1-2), הזרם במעגל הוא סופרפוזיציה של תנודות חופשיות ומאולצות - כשתדירות הכא"מ החיצוני [math]\displaystyle{ \omega }[/math] שווה לתדירות העצמית [math]\displaystyle{ \omega_0 }[/math], משרעת הזרם גדלה באופן מתמיד עד לערך קבוע. כשהתדירויות הנ"ל שונות זו מזו, תיווצר סופרפוזיציה של תנודות חופשיות ומאולצות שתגרום לפעימות דועכות. תדירות הפעימות היא ההפרש שבין תדירות המתח המאלץ לבין תדירות התנודות העצמיות. הזמן בו מגיעה המשרעת לערך קבוע תלוי בגורם האיכות של המעגל: עם הגדלת גורם האיכות, מתארך זמן דעיכת הפעימות, כי זמן דעיכת התנודות החופשיות גדל.

המשוואה הדיפרנציאלית המבטאת את שינוי הזרם במעגל תנודות מאולצות מבוססת על חוק קירכהוף למעגל סגור:

[math]\displaystyle{ {{d^2I} \over dt^2}+{{RdI} \over {Ldt}}+{I \over {LC}}=E_0 \cos \omega t }[/math]

הפתרון הכללי של המשוואה הזאת הוא סכום של הפתרון הכללי של המשוואה ההומוגנית המתאימה (כאשר הצד הימני שווה לאפס) ופתרון פרטי של המשוואה הכללית הנתונה. הפתרון הכללי של המשוואה ההומוגנית מתאר תנודות חופשיות. הפתרון הפרטי של המשוואה הכללית מכיל תנודות של הזרם במעגל, במצב בו התנודות החופשיות כבר חדלו להתקיים. צורתו של הזרם במעגל זה נתון על ידי :[math]\displaystyle{ I=I_0 \cos (\omega t - \phi) }[/math]. כאשר: משרעת הזרם [math]\displaystyle{ I_0 }[/math] היא: [math]\displaystyle{ I_0={E_0 \over {\sqrt {R^2+( \omega L -{1 \over { \omega C}})^2}}} }[/math].

זווית המופע [math]\displaystyle{ \phi }[/math] היא [math]\displaystyle{ \tan \phi={ (\omega L - (\omega C)^{-1}) \over R} }[/math].

מערכת הניסוי

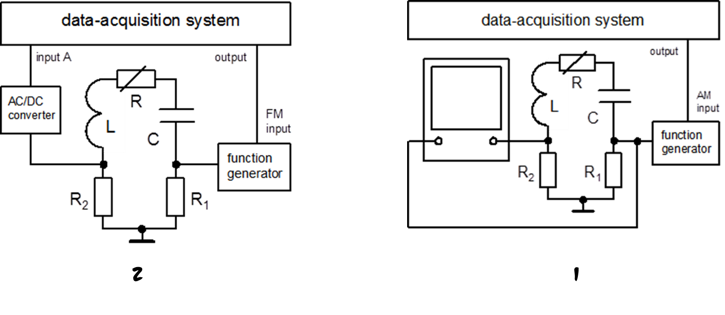
איור 2 מציג את מעגלי המדידה, כאשר איור 2-1 הוא עבור החלק האיכותי של הניסוי ואיור 2-2 הוא עבור החלק הכמותי של הניסוי.

בחלק האיכותי של הניסוי נבחן את תהליכי המעבר של תנודות מאולצות ומרוסנות במעגל-[math]\displaystyle{ RLC }[/math] על מסך האוסצילוסקופ. לשם כך נאפנן את המתח החיצוני באות ריבועי בתדירות גבוהה, לכן על הנגד הקטן [math]\displaystyle{ R_1 }[/math] נוצר באופן מחזורי מתח בתדירות גבוהה. בנוסף ל-[math]\displaystyle{ R_1 }[/math] מחברים בטור: סליל [math]\displaystyle{ L }[/math], קבל [math]\displaystyle{ C }[/math], נגד משתנה [math]\displaystyle{ R }[/math] ונגד קטן [math]\displaystyle{ R_2 }[/math]. המתח מהמתנד משמש כמקור מתח חיצוני, והמתח הנוצר על הנגד [math]\displaystyle{ R_2 }[/math] פרופורציוני לזרם במעגל. אם מודדים את המתח על נגדים [math]\displaystyle{ R_1 }[/math] ו- [math]\displaystyle{ R_2 }[/math] באמצעות הסקופ, ניתן לקבל במקביל את התלות בזמן של הכא"מ החיצוני מהמתנד ואת הזרם במעגל.

איור 2 - מערכת הניסוי: חלק איכותי (1) חלק כמותי (2)

מהלך הניסוי

חלק איכותי

על מנת ליצור גל ריבועי משתמשים במתח אותו מספק הממשק המופעל על ידי ה-Output Signal generator . האות נכנס אל מחולל האותות (Function generator) המוציא גל סינוס. כך נבנית מודולציה ע"י איפנון משרעת AM. אפנון זה מאפשר לנו לראות בסקופ התנהגות תחת כוח מאלץ (מתח חיצוני). את תדירות הגל הריבועי יש לקבוע על [math]\displaystyle{ 2000Hz }[/math] עם משרעת של [math]\displaystyle{ 5 V }[/math]. מחולל האותות מוציא גל sin בתדירות בטווח [math]\displaystyle{ 100 KHz }[/math]. יש לשים לב שמצב האפנון הוא AM.

בהתנגדות מקסימלית ומינימאלית של הנגד המשתנה, מצאו את תדירות הרזוננס של המעגל. עשו זאת על ידי הבחנה בתכונותיהם של התנודות המתקבלות ותהליכי המעבר.

• צלמו את המתקבל בסקופ ודונו מתוצאות המתקבלות.

חלק כמותי

בחלק זה נבחן את תופעת התהודה העומדת בבסיסם של שימושים במעגלי [math]\displaystyle{ RLC }[/math] כמסננים שונים. לשם ביצוע חלק זה אנו נסרוק תדרים במחולל סביב תדר התהודה.

נשתמש בשיטה של "מתח שולט על תדר" (VCF - voltage control frequency). המחולל יוצר תנודות סינוס בתדר התלוי במתח הנכנס, כאשר את מתח האפנון הנכנס למחולל קובעים ע"י הממשק. יש להעביר את המחולל לתצורה של אפנון תדר (FM), ולסרוק את התדרים על ידי סריקה של ערכי המתח היוצא מן הממשק. שנו את המתח על ידי בחירת סוג האות ב-Output Signal generator ל-sin, בתדר [math]\displaystyle{ 0.02 Hz }[/math], וקבלו את אמפליטודת האות היוצא מהממיר AC/DC כפונקציה של התדר במחולל.

כדי לכייל את תלות התדר במתח, נניח כי המתח תלוי בתדר לינארי כמו: [math]\displaystyle{ f=av+b }[/math]. למציאת המקדמים, העבירו את מחולל האותות מהממשק ל-DC. והפעילו 2 ערכי מתח ישר (למשל [math]\displaystyle{ -+2V }[/math]), מצאו את התדרים המתקבלים במחולל ופתרו את צמד המשוואות.

בנו גרפים לתופעת התהודה עבור התנגדות מקסימאלית ומינימאלית במעגל, ודנו בתוצאות.