שימור תנע קווי: הבדלים בין גרסאות בדף
אין תקציר עריכה |
|||
| שורה 39: | שורה 39: | ||
[[קובץ:מערכת הניסוי תנע קווי.png|100px|שמאל|מסגרת|איור 1 - מערכת הניסוי]] | [[קובץ:מערכת הניסוי תנע קווי.png|100px|שמאל|מסגרת|איור 1 - מערכת הניסוי]] | ||
המערכת מורכבת ממסלול שיגור לכדור הפגיעה הבנוי כמסילה משופעת שבסופה חלק אופקי, ראו איור 1. בקצה המסילה ישנה תושבת לכדור נוסף (כדור המטרה), כאשר ההתנגשות בין הכדורים מתרחשת במישור האופקי בלבד. מסלול השיגור מורכב על השולחן, כאשר על הרצפה מונח גיליון נייר ונייר פחם. מנקודת השיגור ישתלשל חוט עם משקולת, שבעזרתם ניתן יהיה לסמן את נקודת ההתנגשות | המערכת מורכבת ממסלול שיגור לכדור הפגיעה הבנוי כמסילה משופעת שבסופה חלק אופקי, ראו איור 1. בקצה המסילה ישנה תושבת לכדור נוסף (כדור המטרה), כאשר ההתנגשות בין הכדורים מתרחשת במישור האופקי בלבד. מסלול השיגור מורכב על השולחן, כאשר על הרצפה מונח גיליון נייר ונייר פחם. מנקודת השיגור ישתלשל חוט עם משקולת, שבעזרתם ניתן יהיה לסמן על גיליון הנייר את ראשית הצירים היא נקודת ההתנגשות. | ||
נתונים שני סוגי כדורים, כדור מתכת וכדור זכוכית השונים זה מזה במסות שלהם. | נתונים שני סוגי כדורים, כדור מתכת וכדור זכוכית השונים זה מזה במסות שלהם. | ||
==מהלך הניסוי== | |||
שחררו גולת מתכת אחת, עקבו אחר תנועתה. בדקו היכן היא פוגעת ברצפה, בעזרת זיהוי מקום הפגיעה על גליון הנייר. חזרו על הניסוי מספר פעמים עד לקבלת מקבץ מאפיין. שרטטו חץ שתחילתו בעקב האנך וסופו במרכז המקבץ, ומדוד את אורכו. | |||
* חשב את רכיב התנע האופקי של הכדור באמצעות אורך החץ הנ"ל. בחישוב יש צורך בידיעת גובה הכדור בזמן בו הוא עוזב את המסילה. | |||
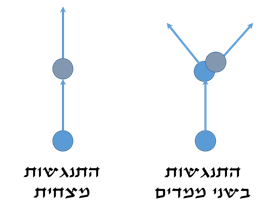
===התנגשות מצחית בין מסות שוות=== | |||
הנח גולה נוספת בקצה המגלשה כך שתיווצר פגיעה "מצחית". שחרר גולה זהה מראש המסילה. היכן נמצאת כל גולה לאחר פגיעתה ברצפה? הסבר! (הראה מקבץ מאפיין). סמן חצים ובדוק את הרכיב האופקי של התנע עבור כל גולה. | |||
[[קובץ:התנגשות.png|100px|שמאל|מסגרת]] | |||
שאלה 2. האם רכיב התנע האופקי נשמר? | |||
שאלה 3. האם ההתנגשות היא אלסטית? הוכח! | |||
גרסה מ־13:52, 23 בפברואר 2015
ניוטון הגדיר את התנע כוקטור השווה למכפלת המסה במהירות, או בסימון מתמטי: [math]\displaystyle{ \vec p=m\vec v }[/math],
כאשר [math]\displaystyle{ m }[/math] היא המסה ו [math]\displaystyle{ \vec v }[/math] הוא וקטור המהירות. חוק שימור התנע קובע כי במערכת סגורה (מערכת בה לא פועלים כוחות חיצוניים) נשמר התנע הכולל:
[math]\displaystyle{ \sum_i m_i \cdot \vec v_i(t) = const }[/math].
בניסוי זה נוכיח את חוק שימור התנע בשני ממדים באופן ניסיוני.
רקע תיאורטי
חוק שימור התנע הוא חוק וקטורי אשר מתקיים לכל אחד מן הצירים בנפרד. לכן ניתן לחלק את הבעיה לשני צירים מאונכים ולפתור עבור כל ציר בנפרד. ניתן לבחון את חוק שימור התנע באמצעות התנגשויות.
התנגשות אלסטית
התנגשות שאין בה איבוד אנרגיה קינטית לטובת חום כתוצאה מהמפגש בין המסות, נקראת התנגשות אלסטית. שתי המשוואות המתארות התנגשות זו הן משוואת אנרגיה ותנע.
כאשר שתי מסות [math]\displaystyle{ m_1, m_2 }[/math] מתנגשות במהירויות [math]\displaystyle{ v_1, v_2 }[/math] בהתאמה. נקבל משוואת שימור תנע: [math]\displaystyle{ m_1 \vec v_1+m_2 \vec v_2=m_1 \vec u_1+m_2 \vec u_2 }[/math] ,
כאשר [math]\displaystyle{ u_1, u_2 }[/math] הן המהירויות של המסות לאחר ההתנגשות.
בנוסף כיוון שההתנגשות אלסטית נקבל גם משוואת שימור אנרגיה: [math]\displaystyle{ \frac {1}{2}m_1 {\vec v_1}^2+\frac {1}{2}m_2 {\vec v_2}^2=\frac {1}{2}m_1 {\vec u_1}^2+\frac {1}{2}m_2 {\vec u_2}^2 }[/math]
התנגשות פלסטית
התנגשות שבה המסות המתנגשות נצמדות זו לזו, נקראת התנגשות פלסטית. עקב ההתנגשות יש איבוד אנרגיה לטובת חום, ולכן האנרגיה הקינטית לא נשמרת. שימור התנע מתקיים.
שתי ההתנגשויות שתוארו להלן הן שתי הקצוות של הסקאלה. יכולה להיות התנגשות שאיבוד החום בה קטן ולכן היא בקרוב אלסטית או ההפך.
בניסוי שלהלן ההתנגשויות הן אלסטיות (בקירוב טוב). כלומר, יש איבוד קטן יחסית של אנרגיה לטובת חום כאשר הכדורים מתנגשים.
מערכת הניסוי
המערכת מורכבת ממסלול שיגור לכדור הפגיעה הבנוי כמסילה משופעת שבסופה חלק אופקי, ראו איור 1. בקצה המסילה ישנה תושבת לכדור נוסף (כדור המטרה), כאשר ההתנגשות בין הכדורים מתרחשת במישור האופקי בלבד. מסלול השיגור מורכב על השולחן, כאשר על הרצפה מונח גיליון נייר ונייר פחם. מנקודת השיגור ישתלשל חוט עם משקולת, שבעזרתם ניתן יהיה לסמן על גיליון הנייר את ראשית הצירים היא נקודת ההתנגשות. נתונים שני סוגי כדורים, כדור מתכת וכדור זכוכית השונים זה מזה במסות שלהם.
מהלך הניסוי
שחררו גולת מתכת אחת, עקבו אחר תנועתה. בדקו היכן היא פוגעת ברצפה, בעזרת זיהוי מקום הפגיעה על גליון הנייר. חזרו על הניסוי מספר פעמים עד לקבלת מקבץ מאפיין. שרטטו חץ שתחילתו בעקב האנך וסופו במרכז המקבץ, ומדוד את אורכו.
- חשב את רכיב התנע האופקי של הכדור באמצעות אורך החץ הנ"ל. בחישוב יש צורך בידיעת גובה הכדור בזמן בו הוא עוזב את המסילה.
התנגשות מצחית בין מסות שוות
הנח גולה נוספת בקצה המגלשה כך שתיווצר פגיעה "מצחית". שחרר גולה זהה מראש המסילה. היכן נמצאת כל גולה לאחר פגיעתה ברצפה? הסבר! (הראה מקבץ מאפיין). סמן חצים ובדוק את הרכיב האופקי של התנע עבור כל גולה.
שאלה 2. האם רכיב התנע האופקי נשמר? שאלה 3. האם ההתנגשות היא אלסטית? הוכח!