שיחה:88-195 בדידה לתיכוניסטים קיץ תשעב
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
שאלה 3 בש.ב
בסעיף ארבע בשאלה זו מורידים את הנקודון פי מקבוצת החזקה של A דבר זה ישפיע רק אם פי נמצאת בקבוצה A ודבר זה לא כתוב. איך אני יכול לדעת האם אני צריך להחסיר עוד אחד או שלא? האם פי היא איבר בA?
- שים לב, זה לא משנה אם הקבוצה הריקה היא איבר ב-A או לא. [math]\displaystyle{ \{A\} }[/math] הוא הנקודון שמכיל את A ולא הקבוצה A עצמה, יש הבדל. --ארז שיינר
אתה יכול להסביר את זה עוד פעם?
- תרשום במפורש את איברי הקבוצה P(A) כאשר A={1,2}. ואחר כך תחסיר ממנה את [math]\displaystyle{ \{\phi\} }[/math]. מה קיבלת? --Grisha 17:08, 19 ביולי 2012 (IDT)
אההה אוקי.
שאלה 6 בשעורי בית
בכל הסעיפים צריך להוכיח או להפריך האם היחסים הבאים הם יחסי שקילות, אבל לא רשמו על איזו קבוצה הם יחסי שקילות עליה.
- רשום שיחסים מוגדרים על קבוצה A. זה לא משנה מהם איברים של A. --Grisha 16:56, 19 ביולי 2012 (IDT)
אוקי הבנתי.
שאלה 3
בשאלה 3 סעיף 4 מה הסדר פעולות של חיסור לא אמור להיות סוגריים על מה שמחסרים קודם????
- זה בדומה לפעולת חיסור הרגילה - אם אתה כובת a-b-c, אתה מבצע את זה לפי סדר ההופעה משמאל לימין. גם כאן זה לפי סדר ההופעה. --Grisha 16:58, 19 ביולי 2012 (IDT)
שאלה 3 סעיף 5
איך ניתן לחשב את מספר האיברים באיחוד שבין שתי הקבוצות? חישבתי את מספר האיברים של כל קבוצה בנפרד (בלי סימן האיחוד ביניהן), אבל אני לא יודע איך להמשיך.
- תנסה לחשב את זה עבור 2-3 דוגמאות. תחשוב כמה איברים שונים וכמה משותפים יש בקבוצות אלה. --Grisha 19:26, 19 ביולי 2012 (IDT)
עשיתי שלוש דוגמאות שונות, וקיבלתי שלוש תוצאות שונות. פעם אחת כל האיברים היו משותפים, בפעם אחרת רק 8 מתוך 16, ובפעם השלישית רק 4 מתוך 16...
- ברור שיצאו מספרים שונים. תנסה להבין מהו קשר בינם לבין k, m ו- n. או תיעזר בדיאגרמות ון. --Grisha 22:36, 19 ביולי 2012 (IDT)
עדיין לא הבנתי את הסעיף, אפשר לקבל כיוון נוסף? לא הצלחתי להבין איך מחשבים את האיחוד או החיתוך של שני הצדדים.
לא מתרגל- אנסה לעזור..אם יש לך איחוד של קבוצות נגיד תרצה לחשב את האיחוד של {1,2},{1,2,3} האיחוד שלהם הוא {1,2,3}. בקבוצה הראשונה יש 2 איברים ובשנייה יש 3 ואם נחבר סה"כ 5, אך ספרנו את מה שמשותף פעמיים (את 1 ו-2 במקרה הזה)- מה שניתן לראות גם בדיאגרמת וון ולכן נרצה להוריד זאת. ומכאן נגיע שאיחוד הקבוצה שווה לחיבור של העוצמה של קבוצה a ועוד העוצמה של b פחות החיתוך בינהן. או בדוגמא שלנו- 5-2=3 סה"כ 3 איברים באיחוד מה שמתאים לעוצמה של {1,2,3}.מקווה שעוזר. והחיתוך נתון בשאלה אז פשוט נעזרים בזה.
שאלה 7.ב'
האם בסעיף הזה מספיק להוכיח כי "X\(X\A) = A" ?
- אם זה כולל הסבר למה זה שקול למה ששואלים, אז כן. --Grisha 22:39, 19 ביולי 2012 (IDT)
רגע אז בעצם למה הם מתכוונים באיחוד המשותף הזה, עוברים איבר איבר ב X/A ומחסירים את X מהאיבר הזה? אם כן הזה זה דיי טריויאלי שזה באמת X/(X/A) = A .
- אז תכתוב את זה מסודר. --Grisha 19:49, 20 ביולי 2012 (IDT)
שאלה 6
האם לדוגמא בסעיף ב' הכוונה ב '/' זה החיסור של קבוצות או קבוצת המנה?
- בשאלה זו השתמשנו ב- \ שמשמעותו הפשר של קבוצות. קבוצת המנה רושמים אחרת, עם /. --Grisha 13:08, 20 ביולי 2012 (IDT)
שאלה 5
לא הבנתי מה זה R, נגיד [math]\displaystyle{ A=\{1,2,3\} }[/math] ו [math]\displaystyle{ A2=\{2,3\} }[/math] [math]\displaystyle{ A1=\{1,2\} }[/math] אז למה שווה R? ל [math]\displaystyle{ \{(1,2)(2,1),(2,2),(2,3),(3,2),(3,3)\} }[/math] ?
- כמעט. אבל אלה לא כל האיברים. --Grisha 16:45, 20 ביולי 2012 (IDT)
אז למה שווה R?
- חסר לך איבר אחד. --Grisha 21:17, 20 ביולי 2012 (IDT)
מה אם כך חסר ב R? ולא הבנתי את הניסוח של R, מה זאת אומרת שקיים i עבורו x,y נמצאים בו? זה בעצם להגיד שהוא לא קבוצה ריקה
- זה אומר זוג סדור (x,y) שייך ל- R רק אם גם x וגם y שייכים לאותה קבוצה [math]\displaystyle{ A_i }[/math]. --Grisha 17:38, 21 ביולי 2012 (IDT)
לפי מה שהבנתי מהשאלות והתשובות: zzz R=A*A zzz (להתעלם מה- Z ) כלומר - R היא המכפלה הקרטזית של A ? וכתוב ש R מוגדר עבור Ai שמקיים( משהו- לא רלוונטי ) - הכוונה ב Ai היא לכל ה- A1 עד An ? ועוד שאלה : הגדרנו בכיתה שאיחוד אוסף על תתי הקבוצות של A הוא A - לכן סעיף ב הוא לא מיותר? ואם לא, האם איחוד אוסף כל תתי הקבוצות של קבוצה ייתן את הקבוצה הגדולה ("המקורית " ) ?
- בואו נדייק. R הוא תת-קבוצה של [math]\displaystyle{ A\times A }[/math] ולאו דווקא שווה לה. לא כתוב ש- [math]\displaystyle{ A_i }[/math] מקיים משהו, להיפך, כתוב שזוג סדור (x,y) שייך ל- R רק אם גם x וגם y שייכים לאותה קבוצה [math]\displaystyle{ A_i }[/math], כאשר i יכול להיות מספר טבעי כלשהו בין 1 ל- n. כלומר "קיים" ולא "לכל".
- לגבי השאלה השניה - לא כתוב בשאלה שאיחוד כל [math]\displaystyle{ A_i }[/math] נותן קבוצה A. זאת כיוון שלא מדברים על "כל" תת-קבוצות אלא רק על אוסף מסוים. --Grisha 23:37, 22 ביולי 2012 (IDT)
תרגיל 2 שאלה 5
בסעיף א' צריך להוכיח או להפריך.. לכאורה צריך להביא מקרה בו ימין נכון ושמאל לא כדי להפריך, וכדי להוכיח מספיק לי להראות ששמאל תמיד נכון?
- על מנת להוכיח צריך להראות שאם ימין נתון שמאל בהכרח נכון, כן. --ארז שיינר
שאלה על תרגיל 1 שאלה 4
"לכל איש עם שם יש שם נוסף (שונה מהראשון)" למה צריך לכלול את הקיום של הn גם בצד השני של הגרירה ב"אז" ולא רק את הקיום של השם הנוסף- הn'? הרי כללנו את קיומו כבר בהנחה של ה"אם". תודה.
- תחום הפעולה של כמת [math]\displaystyle{ \exist n }[/math] הוא רק צד אחד של פעולת גרירה. אפשר להוציא אותו מחוץ לסוגריים. --Grisha 11:24, 23 ביולי 2012 (IDT)
תרגיל 2, שאלה 1
אפשר להגיד ש [math]\displaystyle{ (A \cup B)\setminus (A \triangle B)=A \cap B }[/math] נובע מהגדרת ההפרש הסימטרי או שצריך להוכיח את זה?
- זה לא נובע ישירות. כן צריך להוכיח את זה. --Grisha 23:29, 22 ביולי 2012 (IDT)
תרגיל 1 שאלה 3 סעיף ב'
רוצה לוודא שהבנתי את התשובות- אנחנו צריכים להתייחס למשפט 6 כ"אם" ולראות האם 6-->5, מקבל ערך אמת.יצרנו עולם שבו יש רק אדם אחד שאין לו שם ולכן מצד אחד משפט 6 נכון בגלל שf גורר משהו- תמיד נכון. מצד שני שקרי כי נוצר מצב שבו יש שני אנשים- מה שלא נכון לעולם שיצרנו.אז בעצם יוצא מצב "לא מוגדר" שכזה? וזה נופל פה? כי הצד של ה-6 סוג של "לא מוגדר"? מקווה שניסחתי ברור..
- טענה 6 נכונה בעולם שהגדרנו. אם תסתכל על הנוסחא של טענה 6 (בשאלה 2), תראה שהיא מוגדרת [math]\displaystyle{ (\exist n\in\N: R(p,n))\to ... }[/math]. החלק הראשון (לפני גרירה) הינו שקרי ולכן לא משנה מה יהיה אחרי קשר גרירה, כי משקר אפשר להסיק כל דבר וזה יהיה אמת. לכן טענה 6 נכונה ואני אפילו לא מתייחס לשאלה האם קיים בנאדם שני בעולם שלנו. טענה 5 כפי שכתוב בתשובה היא שקרית. ולכן מקבלים ש- [math]\displaystyle{ (6)\to (5) }[/math] שקרית. (בתשובה יש טעות קטנה של מספור הטענות, הועלה קובץ מתוקן)--Grisha 20:49, 23 ביולי 2012 (IDT)
- הבנתי! ואז זה t--> f אז זה false סה"כ. אם לא אכפת לך, אני רוצה לקחת את זה עוד צעד ולשאול:
אם לצורך העניין משפט 5 היה: אם קיימים 2 אנשים אז הם עם אותו שם- אז בעולם שיצרתי זה כן היה גורר. כי אז שוב ההנחה של 6 שגויה ולכן סה"כ הוא אמת (באופן ריק) אבל הפעם גם ההנחה של 5 שגויה (כי אין 2 אנשים בעולם שיצרנו) ולכן נוצר מצב ריק של true גורר true?
- הרעיון נכון. כדי להיות לגמרי בטוח תכתוב במפורש את טענה 5 החדשה שייצרת. --Grisha 06:27, 24 ביולי 2012 (IDT)
חיתוך
אם יודעים משהו על העוצמה של A חיתוך B ניתן להסיק משהו ישירות על העוצמה של (P(A חיתוך (P(B
- וודאי שכן. (P(B נקראת קבוצת חזקה. כמה איברים יש בקבוצה זו אם ב- B יש n איברים? אם אתה לא זוכר מהתרגול/הרצאה, אז תנסה לבדוק את זה עבור n=0,1,2,3. --Grisha 06:29, 24 ביולי 2012 (IDT)
- כנראה שלא ניסחתי את שאלתי טוב,זה זכור לי שזה 2 בחזקת n העוצמה של קבוצת החזקה. רציתי לדעת פשוט במילים אחרות אם אפשר להסיק על העוצמה של p(a) חיתוך p(b) (ביחד) מהעוצמה של pa חיתוך pb (בנפרד)? זה קשור לשאלה עם ההפרש הסימטרי בין קבוצות החזקה שאלה 3 סעיף 2
-כן.. אפשר כך:
<)math>\left |p(A)\Delta p(B) \right |= \left |(A/B)\cup (B/A) \right |=\left |p(A)/p(B) \right |+\left | p(B)/p(A) \right |-\left | (p(B)/p(A))\cap (p(A)/p(B)) \right |= \left | p(A \right |-\left | p(A\cap B) \right |+\left | p(B) \right |-\left | p(A\cap B) \right |=2^{n}+2^{m}-2\cdot 2^{k}=2^{n}+2^{m}-2^{k+1}</math>
על פי ההגדרה של ההפרש הסימטרי.. --Dvir1352 23:22, 24 ביולי 2012 (IDT)
- שכחת את ()P כמעט בכל מקום. חוץ מזה לא הבנתי לאן נעלם [math]\displaystyle{ \left | (B/A)\cap (A/B) \right | }[/math] --Grisha 01:29, 25 ביולי 2012 (IDT)
ניסיתי לתקן וכל הכתב התחרבש.. בעקרון ברור שהחיתוך של מה שרשמת ריק, מוכיחים את זה בקלות.. עם הנחה בשלילה
שאלה 5
לא הבנתי מה אמור להיות R.. ומה זאת אומרת "קיים i עבורו X ו Y שייכים אליו"... ברור שקיימים אצלו Xו Y כל עוד הוא לא קבוצה ריקה..
לא הבנתי מה זה היחס הזה, ולמה אמרו "קיים i"..
- כתוב בשאלה שזוג סדור (x,y) שייך ל- R רק אם גם x וגם y שייכים לאותה קבוצה [math]\displaystyle{ A_i }[/math], כאשר i יכול להיות מספר טבעי כלשהו בין 1 ל- n. אני ממליץ לעבור עוד הפעם על ניסוח השאלה ולבנות איזשהו יחס שמקיים את התכונות שהוגדרו. גם מומלץ לבדוק שאלות שכבר נענו, יכול להיות שהיה כבר משהו דומה - [[1]]. --Grisha 19:00, 24 ביולי 2012 (IDT)
אבל מהם x ו y? זה סתם מספרים? כי אם הקבוצה לא ריקה אז קיימים בה x,y... מה זאת אומרת "קיים i?"
- i זה אינדקס של קבוצה [math]\displaystyle{ A_i }[/math], כך ש- [math]\displaystyle{ x,y \in A_i }[/math]. חוץ מזה, x ו- y לא חייבים להיות מספרים, הם איברי קבוצה שאתה לא יודע. --Grisha 20:34, 24 ביולי 2012 (IDT)
אבל למה רשמו "קיים i"? והאם זה בעצם במילים אחרות איחוד של קבוצות החזקה של Ai?
- זה לא קשור בכלל לקבוצות חזקה. כתוב קיים i כי קיים i כזה ש- [math]\displaystyle{ x,y \in A_i }[/math]. זה אומר למעשה שקיימת קבוצה [math]\displaystyle{ A_i }[/math] מסוימת.
- אם, לדוגמא, [math]\displaystyle{ x\in A_1 \and y\in A_3 }[/math] אז זוג סדור (x,y) לא שייך ליחס R. --Grisha 01:33, 25 ביולי 2012 (IDT)
שאלה 9
הטבעיים זה כולל אפס או לא כולל? m ו-n לא חייבים להיות שונים נכון? למשל בהוכחה של הרפלקסיביות...
- [math]\displaystyle{ \N }[/math] מתחיל מ- 1. לא כתוב ש- [math]\displaystyle{ m\ne n }[/math] לכן אפשר להניח הכל. --Grisha 20:31, 24 ביולי 2012 (IDT)
בוחן- 1.8
שלום, ידוע כבר איזה נושאים הבוחן יכלול? תודה מראש.
- כל מה שנלמד מתחילת הסמסטר עד השבוע הזה. --Grisha 14:20, 26 ביולי 2012 (IDT)
- תשובת המרצים: כל החומר עד פונקציות וכולל פונקציות, למעט תמונה ותמונה הפוכה. --אוריה 21:53, 28 ביולי 2012 (IDT)
תודה לכם :)
תרגיל 3 שאלה 1 סעיף ב
בסעיף ב' נתון היחס R שהוא עם x,y עכשיו השאלה היא , למי שייכים הx והy? ל A ? לB?
- למעלה, לפני הסעיפים, כתוב כי R הוא יחס על A. --Grisha 18:53, 26 ביולי 2012 (IDT)
שאלה 3 בש"ב 3
כשאומרים שצ"ל ש S יחס סדר על Y, זה אומר שצריך להוכיח שהוא יחס סדר מלא או חלקי?
- כשאומרים יחס סדר זה תמיד יחס סדר חלקי. --Grisha 19:38, 26 ביולי 2012 (IDT)
שאלה 2
בשאלה 2 כשמבקשים לימצוא את יחסי הסדר 1)מדובר על יחס סדר חלקי או מלא? 2)צריך ליכתוב את הפיתרונות או גדול שווה קטן שווה וכו?
- יחס סדר הוא יחס סדר חלקי; לא הבנתי מה זה פתרונות ולמה מה אתה מתכוון כשאומר קטן שווה. --Grisha 20:04, 26 ביולי 2012 (IDT)
שאלה 7 ג' בש"ב 3
מה זאת אומרת שאני צריך לפתור עבוד X כללית? אם לדוגמא אני רוצה להוכיח שהפונקציה לא חח"ע, אני לא יכול להביא בתור דוגמא X ו V מסויימים ולהראות שבמקרה הזה זה לא חח"ע?
- בדיוק. לא ניתן לבחור X מסויימת כאשר מביאים דוגמא נגדית. --אוריה 22:06, 26 ביולי 2012 (IDT)
אוקי עכשיו עוד משהו, כתוב ש V איבר כלשהו ב P(X) (לפי A). אזי מתקיים X/V = X לא? כי ב X קיימים האיברים עצמם, בעוד שב V קיימים הקבוצות שמכילות את האיברים הללו, ולכן אם מחסירים מ X את V מקבלים את X (כי ב V לא קיים שום איבר ב X, אלא רק את הקבוצות המכילות את האיברים הללו (בין היתר))
- [math]\displaystyle{ V }[/math] אינה קבוצת קבוצות אלא תת קבוצה של [math]\displaystyle{ X }[/math]. לכן, [math]\displaystyle{ X\setminus V=X }[/math] אם ורק אם [math]\displaystyle{ V }[/math] קבוצה ריקה. נדמה לי שלא הבנת את נוסח השאלה כראוי. --אוריה 10:10, 27 ביולי 2012 (IDT)
אז בעצם V זה איבר ב P(X)
- כן. כאשר רושמים משהו כמו [math]\displaystyle{ f }[/math] היא פונקציה מ-[math]\displaystyle{ A }[/math] ל-[math]\displaystyle{ B }[/math] המוגדרת ע"י [math]\displaystyle{ f(x)=(\textrm{something...}) }[/math] הכוונה היא ש-[math]\displaystyle{ x\in A }[/math]. --אוריה 12:27, 27 ביולי 2012 (IDT)
תרגיל 3 שאלה 8
מה שצריך לעשות זה להגדיר את g איך שבא לי ואז להראות שהיא אכן פונקציה חח"ע?
- (לא מתרגל/ת): כן.
- כן. --אוריה 22:07, 26 ביולי 2012 (IDT)
תרגיל 3 שאלה 2
1.איך אני יכול להיות בטוח שמצאתי את כל יחסי הסדר וכיצד אני מסביר זאת?
- רמז: הוכחתם בשיעור שבכל קבוצה סדורה לינארית סופית קיים איבר קטן ביותר. אם מסירים אותו הסדר עדיין לינארי ושוב קיים איבר קטן ביותר... --אוריה 10:12, 27 ביולי 2012 (IDT)
2. אם היחס על הקבוצה הוא יחס סדר מלא אז ניתן לסדר את הקבוצה בדיאגרמת הסה כך שהקו המחבר את כל איברי הקבוצה מלמטה למעלה הוא לינארי?
- יחס סדר על קבוצה סופית הוא מלא אם ורק אם דיאגרמת הסה שלו היא בעצם קו ישר (בו כל החיצים מצביעים לאותו כוון). לדוגמא: [math]\displaystyle{ \bullet \to \bullet \to \bullet \to \bullet }[/math]. --אוריה 10:14, 27 ביולי 2012 (IDT)
שאלה 6
סעיפים ב' ו ג' קשורים לסדר המילוני בשאלה (וסעיף א')?
- סעיפים אלה מדברים על יחס סדר R שמוגדר בשאלה. כתוב כי יחס זה נקרא יחס סדר מילוני. --Grisha 14:56, 27 ביולי 2012 (IDT)
אז רגע ה"קטן שווה" שיש בתוך R הוא היחס סדר שמוגדר על A? זה אומר שה"קטן שווה" לא בהכרח קטן שווה על מספרים, אלא סתם מסמן יחס?
- בדיוק. היחס הוא R. "קטן שווה" מסמן יחס סדר כללי. --Grisha 00:56, 28 ביולי 2012 (IDT)
שאלה 5 תרגיל 3
בשאלה 5 מצאתי דוג' נגדית ולכן אני מניח שלא הבנתי נכון את השאלה.. הדוג שלי היא הקב' X={1,2,3,4} והתת קב' A שלי היא: A={1,2,3} והיחס הוא {(1,3)(2,3)(3,3)(2,2)(R={(1,1 כמו שניתן לראות אין כאן סופרימום בניגוד להוכחה שאנחנו צכים להוכיח..
תודה :) תיקנתי
- לא נהוג למחוק דברים שלא אתה כתבת.
- יחס אמור להיות מוגדר על X ולא על A.
- האם זה נכון שיחס סדר שלך הוא יחס "קטן או שווה" רגיל על מספרים שלמים?
- למה אין סופרמום? מה מונע מ- 3 להיות סופרמום? --Grisha 15:37, 27 ביולי 2012 (IDT)
אוקיי סליחה ותודה
שאלה - אם לכל תת קבוצה של קס"ח יש איבר ראשון - הקבוצה הראשית ( הקס"ח ) היא לא בעצם קס"ל כי אם לכל 2 איברים מהקבוצה הראשית אפר לקרוא לאחד מהם איבר ראשון זה אומר שאפשר לבדוק / "להשוות " את מיקום כל אחד מהאיברים ביחס אחד לשני שזו בעצם קבוצה סדורה לינארית
ואם כן , האם מותר להשתמש בנתון שלכל תת קבוצה של X יש איבר ראשון ולכן לכל a,b ששייכים ל X מתקיים: aRb או bRa כנימוק / להוכיח לכך שהקבוצה קס"ל ?
אם לא, אז איך מוכיחים ש - קס"ח היא קס"ל - ,כלומר, מה צריך להוכיח (בנוסף לטרנזיטיבי , אנטי- סימטרי, ורפלקסיבי - הגדרת קס"ח ) ??
תרגיל 3 שאלה 2
כמה יחסי סדר מלאים יש על קבוצה ? 2 בחזקת מספר האיברים ?
- למה אתה חושב ככה? --Grisha 14:54, 27 ביולי 2012 (IDT)
שאלה 6 תרגיל 3
בסעיף ב' כרוצים שנמצא איברים גדולים ביותר ואיברים קטנים ביותר, זה לא נכון יותר לבקש איבר גדול ביותר ואיבר קטן ביותר?
תרגיל 5 כנראה אני לא מבין אותו..
אם לדוגמא נשרטט את דיאגרמת הסה של הקס"ח, נתון שלכל תת קבוצה של X קיים inf, ובפרט חסם מלרע. אבל איך זה הגיוני שלכל תת קבוצה של X קיים חסם מלרע?
אם נסתכל על ה"למעטה" של הדיאגרמה ונבחר את A(תת הקבוצה) להיות האיברים שנמצאים "למעטה", אז לא יכול להיות חסם מלרע ל A במקרה הזה כי לא נמצא מישהו מתחתיהם בדיאגרמה (כי לקחתי את כל המינימאליים).
אפשר הסבר מה הטעות בחשיבה שלי כי אני לא מבין את זה :O
- אני לא הבנתי את הדוגמא שלך. זה שקבוצה נמצאת "למעטה" עוד לא אומר שאין חסם מלרע. ייתכן שאיבר "הכי תחתון" יהיה חסם מלרע וגם אינפימום.
- עוד דבר - ברור שלא כל היחסים מקיימים את זה. אז מה שכתוב בשאלה זה שאנחנו לוקחים רק יחסי סדר שכן מקיימים את התנאי הזה. --Grisha 01:04, 28 ביולי 2012 (IDT)
אוקי תודה ועוד משהו, כתוב שם ש >,X זה קס"ח, וש A זה תת קבוצה של X. אפשר להגיד ש >,A זה גם קס"ח?
- מה אתה חושב על זה? אם אתה חושב שזה נכון, איך היית מוכיח? אם לא - מהי דוגמא נגדית? --Grisha 15:14, 28 ביולי 2012 (IDT)
תרגיל 3 שאלה 8
בתרגיל הנ"ל, אני יכול להניח מראש שf,g,h פונקציות ?
- לגבי g כתוב: "הוכח כי קיימת פונקציה חח"ע" כלומר יש לבנות את g ולהוכיח שמה שבנית זה פונקציה ובנוסף לכך חח"ע.
- לגבי f - אתה צריך להניח כי זאת פונקציה חח"ע. --Grisha 08:52, 28 ביולי 2012 (IDT)
האם אפשר - להגדיר את f כך שהיא תהייה פונקציה חח"ע ?
- למה לא? אתה יכול להגדיר f לפיות פונציה? או איזשהו R להיות יחס שקילות? אז למה אני לא יכול להגיד ש- f היא פונקציה חח"ע? --Grisha 17:18, 29 ביולי 2012 (IDT)
שאלה 6 סעיף ג'
האם זה לא אמור להיות inf של (1,1),(0,1),(0,2) ? או שאין קשר בין סעיף זה לקודמים? פשוט לא הוגדר יחס עם הזוגות האלה, כך שזה קצת לא מובן לי.
- מדובר על איפימום ביחס ליחס הסדר מסעיף ב. (בתחילת סעיף ג רשים "בהנחות של סעיף ב" וזה אומר שסעיף ג הוא המשך ישיר לסעיף ב). --אוריה 21:51, 28 ביולי 2012 (IDT)
אבל האיברים 1,0 ו2,0 לא נמצאים ביחס הסדר המוגדר בסעיף ב'.
- מדובר על היחס [math]\displaystyle{ R }[/math] שמוגדר על הקבוצה [math]\displaystyle{ \{0,1,2\}\times\{0,1,2\} }[/math] לא על היחס [math]\displaystyle{ \leq }[/math] הנתון בסעיף ב. (היחס [math]\displaystyle{ R }[/math] בסעיף ב הוא הסדר המילוני המתקבל מ-[math]\displaystyle{ \leq }[/math]) --אוריה 17:48, 29 ביולי 2012 (IDT)
תרגיל מס' 3 שאלה מס' 1
בסעיף א'- הוכחתי כי היחס הוא יחס שקילות. ואני מנסה למצוא את מחלקות השקילות על קבוצה A=N. כדי לעשות זאת התחלתי לבדוק חוקיות ע"י בחירת מס' קבוע ולבדוק עם אילו מספרים טבעיים מקיים את היחס. יוצא שכל איבר שמכניסים האיבר עצמו נמצא ביחס (נובע גם מהרפלקסיביות) ויוצא שכל n שמכניסים מקיים את היחס עם n+כפולות של 3 וn פחות כפולות של 3. קצת בעייתי לי להבין אם הניסוח הזה של מחלקת שקילות הוא מספיק או שצריך לנסח את זה יותר במדויק? ??
שאלה 3 יחס סדר
כשאומרים יחס סדר, מתכוונים ליחס סדר מלא או חלקי? --Avital 12:06, 29 ביולי 2012 (IDT)
שאלה 6 סעיף ב
האם יכול להיות שאין איברים גדולים ביותר(פשוט בסעיף ג' זה צוין בסוגריים )
- באופן כללי, אם מבקשים למצוא איברים מינימליים, מקסימליים, קטנים וגדולים ביותר זה לא אומר שהם קיימים. --Grisha 14:28, 29 ביולי 2012 (IDT)
שאלה 7 ד' תרגיל 3
לא הבנתי מה עושה f.. היא לוקחת איבר מסויים מ V ומחזירה את ה g שלה, או שהיא לוקחת את כל האיברים ב V , ואז הפלט שמקבל V הוא קבוצה?
- פונקציה f מעתיקה תת-קבוצות של X לתת-קבוצות של Y בעזרת פונקציה g שמעבירה איברים מ- X לאיברים ב- Y. --Grisha 14:40, 29 ביולי 2012 (IDT)
אבל מה זה אומר a איבר ב V? זה אומר ש a מתייחס לאיבר ספציפי ב V או שעושים איחוד לכל איבר ב V?
- זה אומר ש- [math]\displaystyle{ \forall a\in V }[/math] --Grisha 17:15, 29 ביולי 2012 (IDT)
אז זה אומר ש f(V) זה קבוצה?
- כן. כתבתי את זה בתשובה ראשונה (שורה שנייה בהתכתבות זו) --Grisha 18:15, 29 ביולי 2012 (IDT)
שאלה 5
אפשר רמז? :)
( תלמיד/ה ): למתרגלים/מרצים שאלה האם יש אפשרות להוכיח ש- X קס"ל ? - זה יהיה רמז מספיק
באמת חשבתי על לנסות להוכיח את זה :O
- לא הייתי מנסה להוכיח את זה כי זה לא נכון. [math]\displaystyle{ (X,\leq) }[/math] לא חייבת להיות קבוצה סדורה לינארית. לדוגמא, אם [math]\displaystyle{ (X,\leq)=(P(Y),\subseteq) }[/math] אז לכל תת קבוצה לא ריקה של [math]\displaystyle{ X }[/math] יש אינפימום, אבל [math]\displaystyle{ (X,\leq) }[/math] אינה קס"ל. --אוריה 17:53, 29 ביולי 2012 (IDT)
- רעיון יפה, אגב. --אוריה 17:56, 29 ביולי 2012 (IDT)
אפשר אז איזה רמז או משהו?
במה זה zzz p(Y) zzz ? (להתעלם מה- Z )
ולמה זה לא יכול להיות קס"ל ?
כי אם לכל תת קבוצה יש איבר ראשון גם לכל תת קבוצה של שני איברים כלשהם יש איבר ראשון ולכן אפשר ליצור סדר/ יחס בין כל איבר ואיבר, ולפי הנתון שלכל תת קבוצה של X ( כולל X עצמו ) יש איבר ראשון, ולפי ההגדרה של קס"ל - " יהי R קבוצה סדורה חלקית , R יקרא יחס סדר מלא/לינארי אם לכל a,b השייכים לקבוצה , מתקיים aRb או bRa "
ומכיוון שאפשר לקחת כל שני איברים מתת הקבוצה (שיכולה ליהיות גם הקבוצה עצמה )כך שיהיה ביניהם יחס סדר (כי לפי הנתון בטוח אחד מהם איבר ראשון ).
אם יש פה משהו שגוי בבקשה תציינו לי מה כדי שאדע
- בשאלה אומרים שלכל תת-קבוצה לא ריקה A קיים חסם תחתון. לא אומרים שבכל תת-קבוצה יש איבר ראשון. זה לא אותו דבר.
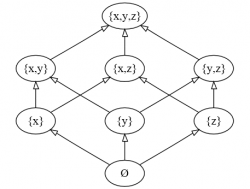
- לדוגמא, האם היחס המוגדר ע"י דיאגרמת הסה הבאה הוא קס"ל או קס"ח? --Grisha 21:00, 29 ביולי 2012 (IDT)
אבל דיאגרמת אסה הזו אינה עומדת בנתון שלכל תת קבוצה יש איבר ראשון -כלומר מה אם אני לוקח את האיברים {x} ו- {y} כתת קבוצה - אין לה איבר ראשון !!! ואפילו לתת קבוצה המכילה את {z} ,{x} , {x,z} אין איבר ראשון ושניהם תתי קבוצות של קבוצה שהופיע בדוגמא וכדי שלכל תת קבוצה יהיה איבר ראשון הקבוצה חייבת ליהיות קס"ל לפי מה שכתבתי למעלה
- אני חוזר ושואל , איפה בניסוח השאלה אתה רואה איברים ראשונים. חסם תחתון זה לא איבר ראשון. --Grisha 22:59, 29 ביולי 2012 (IDT)
תרגיל 3 שאלה 2
לגבי היחס: (4,4),(5,5),(6,6) ,
1. אינו יחס סדר מלא מכיוון שאינו יחס השוואה נכון?
- לא בטוח מה זה יחס השוואה (זה יחס השוויון אם לזה התכוונת), אבל זה אכן לא יחס סדר מלא. --אוריה 17:59, 29 ביולי 2012 (IDT)
הכוונה שלי הייתה שהאיברים לא ניתנים להשוואה ולכן מקיים את כל התנאים של יחס סדר חלקי אך לא של מלא. מקיים רפלקסיביות ומקיים אנטי סימטריות וטרנזטיביות באופן ריק.
2. זה אומר שהוא כן יחס סדר חלקי לצורך העניין?
- היחס הנ"ל הוא יחס סדר חלקי. (אך לא ברור לי מה הנימוך שלך). --אוריה 17:59, 29 ביולי 2012 (IDT)
3. באופן כללי האם צריך איבר אחד בלבד בקבוצה (נגיד a) על מנת שהקבוצה שאני מנסחת מכלל הרפלקסיביות במקרה הזה (a,a)יהווה יחס סדר מלא?
- אם הבנתי נכון, היחס [math]\displaystyle{ \{(a,a)\} }[/math] על הקבוצה [math]\displaystyle{ \{a\} }[/math] הוא באמת יחס סדר מלא. באופן כללי, היחס [math]\displaystyle{ I_X=\{(x,x)|x\in X\} }[/math] הוא יחס סדר מלא אם ורק אם [math]\displaystyle{ |X|=1 }[/math]. --אוריה 17:59, 29 ביולי 2012 (IDT)
הבנת נכון, תודה רבה :)
שאלה לגבי בוחן דמה תשע"א ועוד שתיים לגבי הבוחן ביום ד'
לגבי הבוחן מתשע"א: שאלה 2 ניתנת לפתירה עם כללים שלמדנו ? לגבי הבוחן השנה: א. החלוקה היא לפי ההרצאה? ב. כמה נקודות מוקדשות לכל שאלה?
- כן.
- אתם כותבים את הבוחן בזמן הרצאה.
- ככל הנראה כל השאלות תהיו שווי ערך. במראה ולא, הניקוד יהיה רשום ליד כל שאלה. --Grisha 20:15, 29 ביולי 2012 (IDT)
מאיפה מצאת בחנים?
תשע"א השאלות האחרות הן לגבי הבוחן שיהיה ביום ד' (ושכמובן לא הועלה לאתר)
יש גם בחנים נוספים משנים שעברו?
שאלה 2
איך אני אמור להסביר שאין עוד יחסי סדר מלאים על הקבוצה?
- קודם כל תקרא תשובות לשאלות הקודמות. שאלה זאת כבר נשאלה ונענתה. [[4]] --Grisha 20:06, 29 ביולי 2012 (IDT)
תרגיל 3 שאלה מס' 1
בסעיף א'- הוכחתי כי היחס הוא יחס שקילות. ואני מנסה למצוא את מחלקות השקילות על קבוצה A=N. כדי לעשות זאת התחלתי לבדוק חוקיות ע"י בחירת מס' קבוע ולבדוק עם אילו מספרים טבעיים מקיים את היחס. יוצא שכל איבר שמכניסים האיבר עצמו נמצא ביחס (נובע גם מהרפלקסיביות) ויוצא שכל n שמכניסים מקיים את היחס עם n+כפולות של 3 וn פחות כפולות של 3. קצת בעייתי לי להבין אם הניסוח הזה של מחלקת שקילות הוא מספיק או שצריך לנסח את זה יותר במדויק? ??
- זה נשמע בסדר, רק תגדיר את הקבוצה כמו שצריך. אתה צריך לציין את כל מחלקות השקילות השונות. --אוריה 21:47, 30 ביולי 2012 (IDT)
- אפשר דוג' בבקשה לאיך עושים זאת על קבוצה אינסופית?
תרגיל 3 שאלה 4
הנקודת מוצא בהוכחה הרי צריכה להיות להוכיח הכלה בכיוון שני, נכון? כלומר לקחת איבר ב-S שהוא זוג סדור בעצם כי זה יחס ולהראות כי נמצא ב-R. לא ברור לי איך ניתן להשתמש בנתון על ההכלה מהכיוון הראשון (R מוכל בS) כדי לקשר בינהם. אפשר עצה?
- נצל את העובדה שמדובר ביחסי סדר מלאים. --אוריה 21:48, 30 ביולי 2012 (IDT)
דחוףף
יש לי הארכת זמן ולא קיבלתי מייל לאן אני צריך ללכת כדי להראות שיש לי הארכת זמן מישהו יכול להגיד לי לאן ללכת ועם מה? למי להתקשר?
- דבר עם מלי או עם יעל במזכירות מחר בבוקר: 03-5318407. פניות אישיות כאלה כדאי לשלוח לדוא"ל של המתרגל. --אוריה 21:50, 30 ביולי 2012 (IDT)
תודה!!!,מאיזה שעות בבוקר אפשר להתקשר?
- ב- 8:30 כבר אפשר להתחיל. --Grisha 22:36, 30 ביולי 2012 (IDT)
שאלה על הקבוצה האוניברסלית
האם אני יכול להגדיר את הקבוצה האוניברסלית כקבוצה סופית ולהתייחס רק לקבוצות המוכלות בה? ואם לא איך מוצאים את המשלים של קבוצה בתרגילים כמו הוכח או הפרך
- כן, קבוצה אוניברסלית לא חייבת להיות אינסופית. אתה מדבר על תרגיל מסוים או שואל באופן כללי? --Grisha 22:38, 30 ביולי 2012 (IDT)
פשוט בבוחן דמה משנה שעברה היה צריך להפריך משהו עם משלים ...
שאלה בנושא פונקציות
מה הכוונה שלוקחים פונקציה כך : f: A ->P(P(A))? אם ניקח את הקבוצה A להיות {1,2} מה נקבל ב P(A) כאשר f(1)? ומה נקבל ב P(P(A)?
- לא יודע. תלוי איך אתה מגדיר את הפונקציה. למשל, [math]\displaystyle{ \emptyset }[/math], או [math]\displaystyle{ \{\emptyset\} }[/math] או [math]\displaystyle{ \{\{2\},\{1,2\}\} }[/math] או כל דבר אחר מתוך 16 איברים אפשריים. --Grisha 22:48, 30 ביולי 2012 (IDT)
הפונקציה מוגדרת כך : f(a)מוגדרת להיות : B מוכל ב A כך ש a שייך ל B
- לא הבנתי את הגדרתך. מה זה B? לאן בדיוק מועתקים איברים של A. אם אתה פותר תרגיל כלשהו אז תכתוב את הניסוח המלא שלו; אם זו שאלה כללית אז תנסח אותה ברור יותר. --Grisha 23:43, 30 ביולי 2012 (IDT)
זאת השאלה המלאה: בהינתן קבוצה A נגדיר פונקציה f:A -> P(P(A).ע"י{ f(a):={B [math]\displaystyle{ \subseteq }[/math] A|a [math]\displaystyle{ \in }[/math] B} הוכח או הפרך: f היא חח"ע
תרגיל 3 שאלה 7 סעיף ג'
מי זה v בשאלה?
- פונקציה מקבלת איבר מהתחום ונותנת איבר מהתמונה. כאשר הפונקציה מקבלת את הקבוצה V היא נותנת את הקבוצה X הפרש V. הקבוצה V היא סימון לקבוצה כללית שנכנסת אל הפונקציה, באנלוגיה ל-r ברישום [math]\displaystyle{ f(r)=2r-1 }[/math] --ארז שיינר 11:44, 1 באוגוסט 2012 (IDT)
שאלה 6 - אנטי סימטריות
ניסיתי לחלק את זה למקרים (בטרנזטיביות זה עבד יופי) כלומר סימטריות בהנחה יודעים ש (a,b)R(c,d) וגם (( c,d)R(a,b ואז אפשר לחלק את זה ל-4 מקרים (מכיוון שהשייכות שלהם ליחס מתפצלת בהתאם לתנאי שהם עונים עליו) אחד מהם הוא שמתקיים a קטן שווה מc וגם a שונה מc וגם c קטן שווה מa וגם a שונה מc אבל זה מוביל לסתירה (כי כביכול יוצא a=c u מהאנטי סמטריות של קטן שווה ומצד שני זה וגם a שונה מc) אז זה לא עובד..מה הבעיה? מה ניתן לעשות? תודה.
שאלה מבוחן דמה שפורסם בשנה שעברה
http://up351.siz.co.il/up2/jwnj1ayzy2ew.jpg אשמח לדעת את התשובה לשאלה (כלומר האם צריך להוכיח או להפריך).
לי יצא שזה אמור להיות הפרכה כי המשוואה(הימנית) תמיד נכונה ללא קשר לצד השמאלי ולכן אתה יכול להביא דוגמה לכך שההפרש אינו קבוצה ריקה(ככה שהמשלים שלו אינו הקבוצה האוניברסאלית). *אני סטודנט ולא מרצה/מתרגל אז אם אתה רוצה להיות בטוח אז תחכה שמרצה/מתרגל/מישהו שיודע יותר ממני יענה :) --Avital 20:03, 31 ביולי 2012 (IDT)
(לא מרצה/מתרגל) כן אפשר בקלות להפריך את הטענה הזו..
תרגיל בית 4 שאלה 5
האם אפשר לאמר כי [math]\displaystyle{ f(x)\in f[A] \lt =\gt x\in A }[/math] ?
(תלמיד) - לדעתי כן, זוהי ההגדרה של קבוצת התמונות --גיא 17:09, 4 באוגוסט 2012 (IDT)
תרגיל 4 שאלה 6
בנתון בסוף ש-F(X)εX הסוגריים לא צריכות להיות מרובעות?
- לא. [math]\displaystyle{ f:B\to A }[/math], כאשר [math]\displaystyle{ B\subseteq P(A) }[/math]. כלומר קבוצה X היא איבר בתחום של f. --Grisha 18:11, 4 באוגוסט 2012 (IDT)
תרגיל 4
האם כאומרים הפונקציה מA לA אזי זו פונקצית הזהות של A?
(תלמיד) - לא בהכרח, אפשר לדוגמה להגדיר [math]\displaystyle{ f:Z \to Z }[/math] המוגדרת ע"י [math]\displaystyle{ f(x)=x+1 }[/math]. זוהי פונקציה (ואפילו חח"ע ועל) אך היא לא פונקציית הזהות. --גיא 17:05, 4 באוגוסט 2012 (IDT)
תרגיל 4 שאלה 2
האם בסימן [math]\displaystyle{ \le }[/math] הכוונה היא לסימן הרגיל או המופשט (של יחס כלשהו)?
- מופשט. אינך יודע מהו יחס סדר בקס"ח A ו-B. אפשר לכתוב [math]\displaystyle{ \le_A }[/math] ו-[math]\displaystyle{ \le_B }[/math]. --Grisha 18:14, 4 באוגוסט 2012 (IDT)
שאלה 6
נניח כי [math]\displaystyle{ A=\{ \phi \} }[/math]. מכאן [math]\displaystyle{ p(A)=\{ \phi ,\{ \phi \} \} }[/math]. עכשיו נניח כי [math]\displaystyle{ B=p(A) }[/math].
מהו הערך של [math]\displaystyle{ f(\phi ) }[/math]? הרי מדובר בכל האיברים בפי,והיות ואין בה איברים, זה פי. מצד שני אם זה פי, אז פי איבר של פי, וזו סתירה, כי בפי אין איברים. לכן מתקבל כאן פרדוקס.
"הרי מדובר בכל האיברים בפי". למה זה צריך להיות כל האיברים בפי?
מה שהוכחת פה זה ש f לא חח"ע
שאלה 6
בתרגיל הזה לא כתוב במפורש מה f עושה.. אז בשביל להפריך סעיפים שם אני צריך להביא A ו B מומצאות, ואז להמציא פונקציה f שמקיימת את זה ואז ככה להפריך טענות שם?
ועוד משהו.. לא הבנתי מה זאת אומרת שלכל X ב B מתקיים f(X) איבר ב X..