שדה מגנטי

שדה מגנטי מופק מתנועת מטענים חשמליים, סלילי הלמהולץ הם מערכת של זוג סלילים כאשר מהסופרפוזיציה של השדות שלהם מקבלים שדה מגנטי אחיד בינהם. במעבדה זו נחקור את תכונותיו של השדה המגנטי, הנוצר ע"י שני סלילים זהים הנושאים זרם חשמלי. כמו כן נבחן את הכח הפועל על תיל נושא זרם בשדה מגנטי אחיד.

רקע תיאורטי

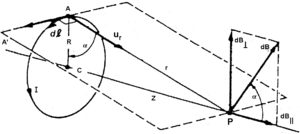
אלמנט אורך אינפיניטסימלי [math]\displaystyle{ dl }[/math] של מוליך הנושא זרם חשמלי [math]\displaystyle{ I }[/math], יוצר בנקודה במרחב הנמצאת במרחק [math]\displaystyle{ r }[/math] מהאלמנט [math]\displaystyle{ dl }[/math] שדה מגנטי [math]\displaystyle{ dB }[/math] . גודל שדה זה ניתן במשוואה וקטורית, הקרויה חוק ביו-סבר :

[math]\displaystyle{ d\vec{B} = \frac{\mu _0}{4\pi} \frac{\ \ q \vec{v} \times \hat{r}}{r^2} = \frac{\mu _0}{4\pi} \frac{I\vec {dl} \times \hat {r}}{r^2} }[/math]

וקטור היחידה [math]\displaystyle{ \hat r }[/math] מכוון מיחידת האורך [math]\displaystyle{ dl }[/math] אל הנקודה. הווקטור [math]\displaystyle{ dl }[/math] מצביע בכיוון הזרם, [math]\displaystyle{ \mu_0=4\pi 10^{-7} TmA^{-1} }[/math] הוא הפרמביליות של הריק. השדה המגנטי של כל המוליך כולו שווה לסכום השדות המגנטיים הנוצרים ע"י כל אלמנטי האורך של מוליך זה.

איור 1 - שדה מגנטי מכריכה

קל לראות כי השדה על צירו של תיל מוליך מעגלי, ברדיוס [math]\displaystyle{ R }[/math] הוא:

[math]\displaystyle{ B={{\mu_0IR^2} \over {2(Z^2+R^2)^{3 / 2}}} }[/math]

כאן [math]\displaystyle{ Z }[/math] הוא המרחק מנקודה על הציר אל מרכז המעגל. מטעמי סימטריה, השדה המגנטי על צירו של זרם מעגלי תמיד מכוון במקביל לציר. השדה המגנטי של סליל דק ( בעל [math]\displaystyle{ N }[/math] כריכות שעוביו קטן בהרבה מרדיוסו שווה לשדה של מוליך מעגלי כשהוא מוכפל ב-[math]\displaystyle{ N }[/math].