פתרון לינארית 2, האונ' העברית, תשסט, סמסטר ב', מוע ד א', חלק ב' שאלה 4
התרגיל:
נתונה המטר': 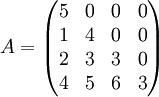
א) מצא את צורת ז'ורדן של A
ב) מצא P הפיכה כך ש 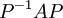 היא צורת ז'ורדן של A.
היא צורת ז'ורדן של A.
מקור: [1]
פתרון:
נתבונן בפולינום האופייני של A (שהוא קל לחישוב, מטר' משולשית): 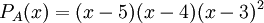 לפי משפט, אותם גורמים לינאריים בדיוק יופיעו בפולינום המינימלי של A.
ברור שהריבוי הגיאומטרי של הע"ע 4,5 הוא 1. כמו כן הגורמים
לפי משפט, אותם גורמים לינאריים בדיוק יופיעו בפולינום המינימלי של A.
ברור שהריבוי הגיאומטרי של הע"ע 4,5 הוא 1. כמו כן הגורמים 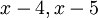 יופיעו בפולינום המינימלי של A [לפי משפט], והמעלה שלהם לא תיהיה גדולה מ 1 כי פולינום מינימלי מחלק כל פולינום שמאפס את A, ובפרט את הפולינום האופייני, לפי משפט קיילי המילטון.
לכן לפי משפט, הבלוקים הגדולים ביותר ביותר המתאימים לע"ע 4,5 הוא החזקה של
יופיעו בפולינום המינימלי של A [לפי משפט], והמעלה שלהם לא תיהיה גדולה מ 1 כי פולינום מינימלי מחלק כל פולינום שמאפס את A, ובפרט את הפולינום האופייני, לפי משפט קיילי המילטון.
לכן לפי משפט, הבלוקים הגדולים ביותר ביותר המתאימים לע"ע 4,5 הוא החזקה של 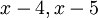 בפולינום המינימלי של A, בהתאמה. ולפי מה שאמרנו זה יהיה שווה בדיוק 1.
לכן צורת ז'ורדן של A היא משהו בסגנון של
בפולינום המינימלי של A, בהתאמה. ולפי מה שאמרנו זה יהיה שווה בדיוק 1.
לכן צורת ז'ורדן של A היא משהו בסגנון של 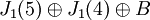
כמו כן, אין עוד בלוקים המתאימים לע"ע 4,5 כי הריבוי הגיאומטרי שלהם הוא בדיוק 1 = כמות הבלוקים שלהם בצורת ז'ורדן.
סך הבלוקים המתאימים לע"ע 3 הוא (ריבוי גאומטרי) כמימד מרחב האיפוס של 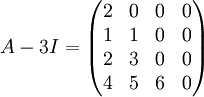 וזו מטר' מדורגת מדרגה 3 מסדר 4, ולכן מימד מרחב האיפוס שלה הוא בדיוק 1, ולכן סה"כ צורת ז'ורדן של A היא:
וזו מטר' מדורגת מדרגה 3 מסדר 4, ולכן מימד מרחב האיפוס שלה הוא בדיוק 1, ולכן סה"כ צורת ז'ורדן של A היא: 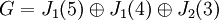
ב) נסמן את העמודות של P ב (v1,v2,v3,v4) בהתאמה. אזי: 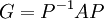 ולכן
ולכן 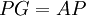 ולכן לכל i רלוונטי
ולכן לכל i רלוונטי 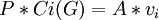 .
.
אז עבור i = 1,2 זה ממש קל כי אנחנו רק צריכים למצוא וקטורים עצמיים שמתאימים לע"ע 4,5... ברור שאנחנו יודעים לעשות את זה, לכן אני אחסוך לכולם[חוץ מלעצמי] חישוב מפרך ונגיע ל 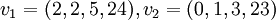 נקבל לפי הנ"ל גם את המשוואות הבאות:
נקבל לפי הנ"ל גם את המשוואות הבאות: 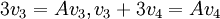 נעביר קצת אגפים ונקבל:
נעביר קצת אגפים ונקבל: 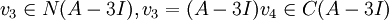 כאשר N מציין את מרחב האיפוס ו C מציין את מרחב העמודות.
כאשר N מציין את מרחב האיפוס ו C מציין את מרחב העמודות.
כבר כתבנו למעלה את A-3I אז אפשר להסתכל עליה.
כבר אמרנו גם שמימד המרחב העצמי של הע"ע 3 הוא 1, ולכן ל 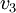 יש לנו רק אפשרות אחת (עד כדי כפל בסקלר שלא מעניין אותנו פה), ממש קל לראות שאותו וקטור הוא
יש לנו רק אפשרות אחת (עד כדי כפל בסקלר שלא מעניין אותנו פה), ממש קל לראות שאותו וקטור הוא 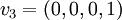 ולכן קיבלנו משוואה:
ולכן קיבלנו משוואה: 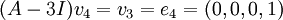 זו משוואה פשוטה למדי בארבעה נעלמים שאפשר לפתור עם דירוג [אגב, אין לזה פתרון יחיד]:
זו משוואה פשוטה למדי בארבעה נעלמים שאפשר לפתור עם דירוג [אגב, אין לזה פתרון יחיד]: 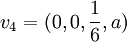 אבל נבחר a = 0 שיהיה נוח לכולם...
אבל נבחר a = 0 שיהיה נוח לכולם... 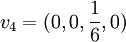
סוף סוף קיבלנו את 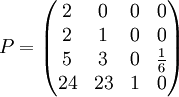 זה מגניב כי אם נחליף את שורה 3,4 אנחנו רואים ש P היא הפיכה [דרגה 4], אז לא דיברנו שטויות לגמרי, יש ניצוץ של תקווה... טוב נו, אם בודקים זה אכן יוצא נכון [סתם עבודה טכנית, שלצערי עשיתי אותה]
זה מגניב כי אם נחליף את שורה 3,4 אנחנו רואים ש P היא הפיכה [דרגה 4], אז לא דיברנו שטויות לגמרי, יש ניצוץ של תקווה... טוב נו, אם בודקים זה אכן יוצא נכון [סתם עבודה טכנית, שלצערי עשיתי אותה]