משתמש:אור שחף/133 - הרצאה/17.5.11
את משפט 10 לא סיימנו בהרצאה הקודמת ולכן השלמנו אותו ב-17.6.11. חלק זה מופיע בסיכום ההרצאה הקודמת ולא בדף הנוכחי.
התכנסות במ"ש של טורים (המשך)
דוגמה
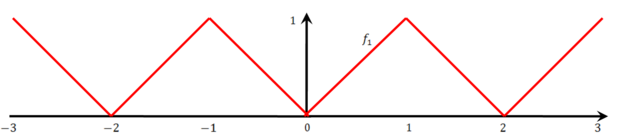
נבנה פונקציה S רציפה ב-[math]\displaystyle{ \mathbb R }[/math] שאינה גזירה באף נקודה. תחילה נגדיר [math]\displaystyle{ f_1(x)=|x| }[/math] בקטע [math]\displaystyle{ [-1,1] }[/math] עם המשך מחזורי בכל [math]\displaystyle{ \mathbb R }[/math]:
לכן [math]\displaystyle{ f_1(x+2)=f_1(x) }[/math] וכן אם [math]\displaystyle{ x\not\in\mathbb Z }[/math] אז [math]\displaystyle{ f_1'(x)\in\{\pm1\} }[/math], ואחרת הנגזרת לא קיימת. כמו כן נגדיר [math]\displaystyle{ f_2(x)=\frac14f_1(4x) }[/math] ואז [math]\displaystyle{ f_2\left(x+\frac24\right)=f_2(x) }[/math] וכן אם [math]\displaystyle{ \frac x4\not\in\mathbb Z }[/math] אז [math]\displaystyle{ f_2'(x)\in\{\pm1\} }[/math]. נמשיך להגדיר [math]\displaystyle{ f_{n+1}(x)=\frac14f_n(4x)=\frac1{4^n}f_1\left(4^nx\right) }[/math] ולכן [math]\displaystyle{ f_{n+1}\left(x+\frac 2{4^n}\right)=f_{n+1}(x) }[/math] ואם [math]\displaystyle{ \frac x{4^n}\not\in\mathbb Z }[/math] אז [math]\displaystyle{ f_{n+1}'(x)\in\{\pm1\} }[/math]. לבסוף, נגדיר [math]\displaystyle{ S(x)=\sum_{n=1}^\infty f_n(x) }[/math] אזי S רציפה ב-[math]\displaystyle{ \mathbb R }[/math] (כי כל [math]\displaystyle{ f_n }[/math] רציפה והטור מתכנס במ"ש עפ"י מבחן ה-M של וירשטרס: [math]\displaystyle{ |f_n(x)|=\left|\frac1{4^n}f_1\left(4^nx\right)\right|\le\frac1{4^n} }[/math] ו-[math]\displaystyle{ \sum\frac1{4^n} }[/math] מתכנס).
הוכחה שגויה לכך שהפונקציה לא גזירה: [math]\displaystyle{ S'(x)=\sum_{n=1}^\infty f_n'(x)=\sum_{n=1}^\infty \pm1 }[/math] שמתבדר (כי [math]\displaystyle{ \pm1\not\to0 }[/math]), ולכן הפונקציה אינה גזירה בשום נקודה. הוכחה זו אינה נכונה כי היא מתבססת על הטענה שאומרת שאם [math]\displaystyle{ f_n\to f }[/math] במ"ש ואם [math]\displaystyle{ \lim_{n\to\infty}f_n' }[/math] לא קיים אז f לא גזירה, טענה שאפשר לסתור בעזרת [math]\displaystyle{ f_n }[/math] שהגדרנו קודם: [math]\displaystyle{ \lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}\frac1{4^n}f_1\left(4^nx\right)=0 }[/math] ולכן הפונקציה הגבולית (שהיא 0) גזירה, אבל [math]\displaystyle{ \lim_{n\to\infty}f_n'(x)=\lim_{n\to\infty}\frac{4^n}{4^n}f_1'(4^nx) }[/math] שמתבדר בין [math]\displaystyle{ -1 }[/math] ל-1, עם ערכים לא מוגדרים באמצע.
הוכחה נכונה: נאמר ששתי נקודות שונות [math]\displaystyle{ x_1,x_2\in\mathbb R }[/math] מקיימות את התכונה [math]\displaystyle{ P_1 }[/math] הן נמצאות בקטע שבין שתי נקודות קיצון סמוכות של [math]\displaystyle{ f_1 }[/math] (למשל הקטע [math]\displaystyle{ [0,1] }[/math], כי הוא נמצא בין נקודות הקיצון שב-0 וב-1, או הקטע [math]\displaystyle{ [-3,-2] }[/math] וכו'). אם [math]\displaystyle{ x_1,x_2 }[/math] מקיימות זאת אזי [math]\displaystyle{ \frac{f_1(x_1)-f_1(x_2)}{x_1-x_2}\in\{\pm1\} }[/math]. נמשיך כך ונאמר ששתי נקודות [math]\displaystyle{ x_1,x_2 }[/math] מקיימות תכונה [math]\displaystyle{ P_n }[/math] אם"ם הן בקטע שבין שתי נקודות קיצון סמוכות של [math]\displaystyle{ f_n }[/math]. במקרה כזה [math]\displaystyle{ \frac{f_n(x_1)-f_n(x_2)}{x_1-x_2}\in\{\pm1\} }[/math]. נשים לב שאם הנקודות [math]\displaystyle{ x_1,x_2 }[/math] מקיימות [math]\displaystyle{ P_n }[/math] אז הן מקיימות [math]\displaystyle{ P_{n-1} }[/math], ובהכללה [math]\displaystyle{ P_n\implies P_{n-1}\implies\dots\implies P_1 }[/math]. כעת יהי [math]\displaystyle{ x\in\mathbb R }[/math] נתון ונוכיח כי [math]\displaystyle{ S'(x) }[/math] לא קיים. מספיק להוכיח שעבור סדרה [math]\displaystyle{ \{h_m\} }[/math] כלשהי כך ש-[math]\displaystyle{ 0\ne h_m\to0 }[/math] לא קיים הגבול [math]\displaystyle{ \lim_{m\to\infty}\frac{S(x+h_m)-S(x)}{h_m} }[/math]. נבחר [math]\displaystyle{ h_m=\frac2{4^m} }[/math] אם [math]\displaystyle{ x,x+\frac2{4^m} }[/math] מקיימות [math]\displaystyle{ P_m }[/math], ו-[math]\displaystyle{ h_m=-\frac2{4^m} }[/math] אחרת. נשים לב שבכל מקרה הנקודות [math]\displaystyle{ x,x+h_m }[/math] מקיימות [math]\displaystyle{ P_m }[/math] כי אם [math]\displaystyle{ x,x+\frac2{4^m} }[/math] לא מקיימות [math]\displaystyle{ P_m }[/math] אזי יש בין שתיהן נקודת קיצון של [math]\displaystyle{ f_m }[/math]. ההפרש בין שיעורי ה-x של שתי נקודות קיצון סמוכות ב-[math]\displaystyle{ f_m }[/math] הוא [math]\displaystyle{ \frac4{4^m} }[/math] ולכן [math]\displaystyle{ x,x-\frac2{4^m} }[/math] כן מקיימות [math]\displaystyle{ P_m }[/math]. כמו כן ברור כי [math]\displaystyle{ 0\ne h_m\to0 }[/math]. מתקיים [math]\displaystyle{ \forall m:\ \frac{S(x+h_m)-S(x)}{h_m}=\sum_{n=1}^\infty \frac{f_n(x+h_m)-f_n(x)}{h_m} }[/math]. כיוון ש-[math]\displaystyle{ x,x+h_m }[/math] מקיימות [math]\displaystyle{ P_m\and P_{m-1}\and\dots\and P_1 }[/math] מתקיימת לכל [math]\displaystyle{ 1\le n\le m }[/math] הטענה [math]\displaystyle{ \frac{f_n(x+h_m)-f_n(x)}{h_m}\in\{\pm1\} }[/math]. עבור [math]\displaystyle{ n\gt m }[/math] המחזור של [math]\displaystyle{ f_n }[/math] הוא [math]\displaystyle{ \frac2{4^{n-1}} }[/math]. אם [math]\displaystyle{ n\gt m }[/math] אז [math]\displaystyle{ h_m=\pm\frac2{4^m}=\pm\frac2{4^{n-1}}\cdot4^{n-m-1} }[/math] הוא מספר שלם של מחזורים, ולכן [math]\displaystyle{ f_n(x+h_m)=f_n(x) }[/math], ומכאן ש-[math]\displaystyle{ \forall n\gt m:\ \frac{f_n(x+h_m)-f_n(x)}{h_m}=0 }[/math]. לפיכך לכל m נקבל [math]\displaystyle{ \frac{S(x+h_m)-S(x)}{h_m}=\sum_{n=1}^m\pm1+\sum0 }[/math]. כאשר [math]\displaystyle{ m\to\infty }[/math] הגבול לא קיים ולכן S לא גזירה ב-x, והטענה נכונה לכל x. [math]\displaystyle{ \blacksquare }[/math]