שיחה:88-133 אינפי 2 תשעב סמסטר ב

חזרה לדף הקורס

גלול לתחתית העמוד

הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

שאלות

מערך שיעור 1

השקעתי מלא, אז בבקשה תפתחו קישור כמו שהיה באינפי למערכי שיעור ותדביקו את זה שם (כולל קרדיט לנמרוד ^_^ )

חקירת פונקציות:

נתונה פונקציה [math]\displaystyle{ f(x) }[/math]. אוספים מידע על [math]\displaystyle{ f }[/math], ובסוף משרטטים את הגרף.

תכנית (אפשרית):

1) תחום הגדרה של [math]\displaystyle{ f(x) }[/math] ונק' מיוחדות (אי-רציפות/גזירות), זוגית/אי-זוגית.

2) מה קורה ל-[math]\displaystyle{ f(x) }[/math] כאשר [math]\displaystyle{ x \to \pm \infty }[/math]. (בפרט אם קיים [math]\displaystyle{ \lim_{x \to \pm \infty }f(x)=a }[/math], [math]\displaystyle{ y=a }[/math] אסימפטוטה אופקית) אם קיימים [math]\displaystyle{ a,b }[/math] קבועים כך ש-[math]\displaystyle{ \lim_{x \to \pm \infty }[f(x)-(ax+b)]=0 }[/math] אז [math]\displaystyle{ y=ax+b }[/math] אסימפטוטה משופעת.

3) אם עבור [math]\displaystyle{ a \in \real }[/math]: [math]\displaystyle{ \lim_{x \to a^\pm }f(x)=\infty \, \, or\, (-\infty) }[/math] אז הישר [math]\displaystyle{ x=a }[/math] אסימפטוטה אנכית.

4) מחשבם את [math]\displaystyle{ f'(x) }[/math] ואיתה תחומי עליה/ירידה של [math]\displaystyle{ f }[/math] ונ' קריטיות.

5) מחשבים [math]\displaystyle{ f''(x) }[/math] ואיתה תחומי קעירות/קמירות ונק' פיתול של [math]\displaystyle{ f }[/math].

6) טבלת ערכים הכוללת נק' חשובות:

[math]\displaystyle{ f(x) }[/math]	[math]\displaystyle{ x }[/math]
.	.
.	.
.	.

7) מסרטטים את הגרף.

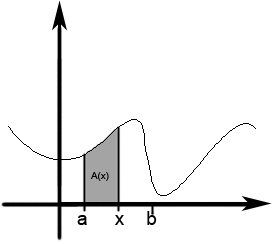
אינטגרלים:

הגדרה: תהי [math]\displaystyle{ f(x) }[/math] פונקציה המוגדרת בקטע כלשהו [math]\displaystyle{ I }[/math]. אומרים שהפונקציה [math]\displaystyle{ F(x) }[/math] קדומה ל- [math]\displaystyle{ f(x) }[/math] ב-[math]\displaystyle{ I }[/math] אם [math]\displaystyle{ F'(x)=f(x) }[/math] לכל [math]\displaystyle{ x \in I }[/math].

משפט 1: תהי [math]\displaystyle{ f(x) }[/math] מוגדרת בקטע I. נניח ש-[math]\displaystyle{ G(x) }[/math] וגם [math]\displaystyle{ H(x) }[/math] קדומות ל [math]\displaystyle{ f }[/math] ב-[math]\displaystyle{ I }[/math] כך שלכל [math]\displaystyle{ x \in I }[/math]: [math]\displaystyle{ G(x)-H(x)=C }[/math].

הוכחה: נגדיר [math]\displaystyle{ F(x)=G(x)-H(x) }[/math], לפי הנתון [math]\displaystyle{ F'(x)=f(x)-f(x)=0 }[/math] עפ"י אחת התוצאות של משפט לגרנג' [math]\displaystyle{ F(x) }[/math] קבועה, ולכן קיימת [math]\displaystyle{ C \in \real }[/math] עבורה [math]\displaystyle{ C=F(x)=G(x)-H(x) }[/math].

סימון מקובל: אם [math]\displaystyle{ F(x) }[/math] קדומה ל-[math]\displaystyle{ f(x) }[/math] כותבים: [math]\displaystyle{ \int f(x)=F(x)+C }[/math] .

[math]\displaystyle{ A(x)=\int f(t) dt }[/math] עבור כל [math]\displaystyle{ x \in [a,b] }[/math] טענה נועזת: [math]\displaystyle{ A(x) }[/math] גזירה ו-[math]\displaystyle{ A'(x)=f(x) }[/math]. הוכחה: [math]\displaystyle{ A'(x)=\lim_{\Delta x \to 0} \frac {A(x+\Delta x)-A(x)}{\Delta x}=f(x) }[/math] כעת, השטח שמתחת לגרף הוא [math]\displaystyle{ A(b) }[/math] (נעיר ש-[math]\displaystyle{ A(a)=0 }[/math]) כעת, תהי [math]\displaystyle{ F(x) }[/math] פונקציה קדומה ל-[math]\displaystyle{ f(x) }[/math] בקטע [math]\displaystyle{ [a,b] }[/math]. כיוון שכבר הוכחנו ש-[math]\displaystyle{ A(x) }[/math] קדומה ל-[math]\displaystyle{ f(x) }[/math], משפט 1 אומר ש- [math]\displaystyle{ F(x)=A(x)+C }[/math]. מכאן ש- [math]\displaystyle{ =\int^b_a f(x) dx }[/math]השטח[math]\displaystyle{ F(b)-F(a)=A(b)+C-[A(a)-C]=A(b)= }[/math].

אינטגרל לא מסויים: אינטגרל בלי גבולות - [math]\displaystyle{ \int f(x)dx }[/math] והתוצאה היא לפי פונקציה הקדומה: [math]\displaystyle{ F(x)+C }[/math].

טבלה של אינטגרלים בסיסיים:

[math]\displaystyle{ F(x) }[/math]	[math]\displaystyle{ f(x) }[/math]
[math]\displaystyle{ \frac {(x+a)^{n+1}}{n+1} }[/math]	[math]\displaystyle{ (x+a)^n \, \, (n \neq -1) }[/math]
[math]\displaystyle{ ln(x+a) }[/math]	[math]\displaystyle{ (x+a)^{-1} }[/math]
[math]\displaystyle{ \sin (x+a) }[/math]	[math]\displaystyle{ \cos (x+a) }[/math]
[math]\displaystyle{ -\cos (x+a) }[/math]	[math]\displaystyle{ \sin (x+a) }[/math]
[math]\displaystyle{ e^{x+a} }[/math]	[math]\displaystyle{ e^{x+a} }[/math]
[math]\displaystyle{ \frac{a^x}{\ln a} }[/math]	[math]\displaystyle{ a^x }[/math]
[math]\displaystyle{ \arcsin x }[/math]	[math]\displaystyle{ \frac {1}{\sqrt{1-x^2}} }[/math]
[math]\displaystyle{ \arctan x }[/math]	[math]\displaystyle{ \frac {1}{1+x^2} }[/math]
[math]\displaystyle{ \arcsin \frac{x}{a} }[/math]	[math]\displaystyle{ \frac {1}{\sqrt{a^2-x^2}} }[/math]
[math]\displaystyle{ \frac{1}{a}\arctan \frac{x}{a} }[/math]	[math]\displaystyle{ \frac {1}{a^2+x^2} }[/math]